- Research
- Open access
- Published:
Financial asset price bubbles under model uncertainty
Probability, Uncertainty and Quantitative Risk volume 2, Article number: 14 (2017)
Abstract
We study the concept of financial bubbles in a market model endowed with a set \({\mathcal {P}}\) of probability measures, typically mutually singular to each other. In this setting, we investigate a dynamic version of robust superreplication, which we use to introduce the notions of bubble and robust fundamental value in a way consistent with the existing literature in the classical case \({\mathcal {P}}=\{{\mathbb {P}}\}\). Finally, we provide concrete examples illustrating our results.
Introduction
Financial asset price bubbles have been intensively studied in the mathematical literature in recent years. The description of a financial bubble is usually built on two main ingredients: the market price of an asset and its fundamental value. As the first is simply observed by the agent, the modeling of the intrinsic value is where the differences between various approaches arise. In the classical setup, where models with one prior are considered, the main approach is given by the martingale theory of bubbles, see Biagini et al. (2014); Jarrow et al. (2010); Loewenstein and Willard (2000) and Protter (2013). According to this theory, the fundamental value is defined as the expected sum of future discounted payoffs under a risk neutral measure. Other approaches within the martingale framework make use of further assumptions, such as portfolio constraints or defaultable claims, to explain how a bubble originates in the market, see Biagini and Nedelcu (2015); Hugonnier (2012) and Jarrow et. al. (2012). Recently, however, another definition has been proposed in Herdegen and Schweizer (2016), where the fundamental value is assumed to be given by the superreplication price of the asset.
In this paper, we aim to contribute to the existing literature by introducing a framework for the formation of bubbles under model uncertainty. We consider a continuous (discounted) asset price S in a market endowed with a set \({\mathcal {P}}\) of local martingale measures for S, which are possibly mutually singular to each other and support a time consistent sublinear expectation. Each one of these priors is to be interpreted as a possible law for the dynamics of S.
The market price will still be exogenous, but the fundamental value S∗ will have a fairly different interpretation from the classical literature and generate unexpected consequences. We describe in fact S∗ by mean of the conditional sublinear expectation of the terminal value of S. By using the characterisation of sublinear operator of Theorem 1, S∗ represents in this way a maximal fundamental value, taking in account of each fundamental value under the different priors. Proposition 1 then shows that aggregation can be done on the set of probability measures having the same family of null sets up to time t, i.e. sharing the same view on the “impossible” events up to time t. A financial interpretation and a strong link with the classical literature on bubble is then provided by Theorem 4, where we study the problem of dynamic superreplication, by extending Theorem 3.2 in Nutz (2015) to the dynamic case. This result provides an extension of the approach of Herdegen and Schweizer (2016) to the case of mutually singular priors.
The resulting bubble, defined as S−S∗, has \({\mathbb {P}}\)-local submartingale dynamics under each \({\mathbb {P}}\)-market for \({\mathbb {P}}\in {\mathcal {P}}\). This generalizes in a natural way the local-martingale dynamics which an asset price bubble displays in classical models under equivalent priors. Furthermore it allows to describe the birth of a bubble and its growth in size in a static model, i.e. without changing the investor’s risk neutral measure over time, similarly to the approach of Herdegen and Schweizer (2016). The same submartingale behavior is in fact described for some cases also in Biagini et al. (2014), but it is the result of a smooth shift from an equivalent pricing measure to another. To the best of our knowledge this description of bubbles is new, as it distinguishes itself also from the robust setting outlined in Cox et al. (2016), where bubbles arise as a consequence of constraints on possible trading strategies in a different setup.
Another interesting feature of our model is the way a bubble is perceived by investors affected by less uncertainty, who are endowed with a smaller set of probabilities \({\mathcal {P}}^{\prime }\subseteq {\mathcal {P}}\). It might in fact happen that a bubble is not seen as such for some particular priors. Alternatively stated, the asset originating the bubble may be a (uniformly integrable) \({\mathbb {P}}\)-martingale for some \({\mathbb {P}}\in {\mathcal {P}}\). In this regard, our results represent an extension of the setting of Herdegen and Schweizer (2016), where market bubbliness excludes the existence of a true martingale measure.
Finally, we investigate the notion of no dominance, proposing its robust counterpart in the model uncertainty framework and studying its consequences on the concept of bubble.
The paper is organized as follows. In “The setting” section, we outline the notation and present an alternative characterization of the conditional sublinear expectation operator in Proposition 1. In “Bubbles under uncertainty” section, after reviewing the existing literature, we discuss and study our concept of robust fundamental value, bubble under uncertainty, and robust no dominance, illustrating our results through concrete examples. In “Infinite time horizon” section, we examine the situation in which the time horizon is not bounded. In the Appendix finally, we study the problem of dynamic superreplication.
The setting
We consider a family \({\mathcal {P}}\) of probability measures, typically non-dominated, on  , the space of càdlàg paths
, the space of càdlàg paths  with ω0=0 endowed with the topology of weak convergence. We denote with \({\mathcal {F}}\) the Borel σ-field on Ω. Given a \({\mathcal {F}}\)-measurable function ξ, we are interested in sublinear expectations
with ω0=0 endowed with the topology of weak convergence. We denote with \({\mathcal {F}}\) the Borel σ-field on Ω. Given a \({\mathcal {F}}\)-measurable function ξ, we are interested in sublinear expectations
inducing time consistent conditional sublinear expectations. For this reason, some conditions have to be enforced both on the set of priors and on the random variables we take into account. Given a stopping time τ of the filtration \({\mathbb {F}}:=\{{\mathcal {F}}_{t}\}_{t\geq 0}\) generated by the canonical process, the main technical issue is to guarantee that the conditional sublinear expectation operator
where the essential supremum is taken with respect to the probability measure \({\mathbb {P}}\) and \({\mathcal {P}}(\tau,{\mathbb {P}})\) denotes the set of probabilities \(\{{\mathbb {P}}^{\prime }\in {\mathcal {P}}\; : \; {\mathbb {P}}^{\prime }={\mathbb {P}}\text {~on~} {\mathcal {F}}_{\tau }\}\) first introduced in Soner et al. (2013), is well-defined. This problem is solved in the literature by means of different approaches, generally by shrinking the set of priors \({\mathcal {P}}\) or by requiring strong regularity of the random variables, see Cohen (2012); Nutz and Soner (2012); Nutz and Van Handel (2013); Peng (2010), and Soner et al. (2011b). We choose to place ourselves in the context of Nutz (2015), as it generalizes the frameworks of G-expectation and random G-expectation and provides some tractability of stopping times, which remains an open question in the G-setting.
For the sake of completeness, we then summarize the notation and the hypothesis we enforce on the set \({\mathcal {P}}\), as stated in Nutz (2015), together with the notation introduced thereby. We start with the definition of polar set.
Definition 1
A set is called polar if it is \(({\mathcal {F}},{\mathbb {P}})\)-null for all \({\mathbb {P}}\in {\mathcal {P}}\). The collection of all polar sets is denoted by \({\mathcal {N}}^{\mathcal {P}}\).
Let \(\mathfrak {P}(\Omega)\) be the set of all probability measures on \((\Omega,{\mathcal {F}})\) equipped with the topology of weak convergence. For any stopping time τ, the concatenation of \(\omega,\tilde {\omega }\in \Omega \) at τ is the path
Given a function ξ on Ω and ω∈Ω, we define the function ξτ,ω on Ω by
For any probability measure \({\mathbb {P}}\in \mathfrak {P}(\Omega)\), there exists a regular conditional probability distribution \(\{{\mathbb {P}}_{\tau }^{\omega }\}_{\omega \in \Omega }\) given \({\mathcal {F}}_{\tau }\), i.e., \({\mathbb {P}}_{\tau }^{\omega }\in \mathfrak {P}(\Omega)\) for each ω, while \(\omega \mapsto {\mathbb {P}}_{\tau }^{\omega }(A)\) is \({\mathcal {F}}_{\tau }\)-measurable for any \(A\in {\mathcal {F}}\) and
whenever ξ is \({\mathcal {F}}\)-measurable and bounded. Moreover, \({\mathbb {P}}_{\tau }^{\omega }\) can be chosen to be concentrated on the set of paths that coincide with ω up to time τ(ω),
We define the probability measure \({\mathbb {P}}^{\tau,\omega }\in \mathfrak {P}(\Omega)\) by
We then have the the identities
We next recall, as in Nutz and Van Handel (2013), some basic notions from the theory of analytic sets. A subset of a Polish space is called analytic if it is the image of a Borel subset of another Polish space under a Borel-measurable mapping. In particular, any Borel set is analytic. The collection of analytic sets is stable under countable intersections and unions, but, in general, not under complementation and therefore does not constitute a σ-algebra.
For each  we fix a set \({\mathcal {P}}(s,\omega)\subseteq \mathfrak {P}(\Omega)\). Assume that
we fix a set \({\mathcal {P}}(s,\omega)\subseteq \mathfrak {P}(\Omega)\). Assume that
and \({\mathcal {P}}(0,\omega)={\mathcal {P}}\) for all ω∈Ω. We next define the universal completion of a σ-field.
Definition 2
Given a σ-field \({\mathcal {G}}\), the universal completion of \({\mathcal {G}}\) is the σ-field \({\mathcal {G}}^{\ast }=\cap _{\mathbb {P}} {\mathcal {G}}^{\mathbb {P}}\), where \({\mathbb {P}}\) ranges over all probability measures on \({\mathcal {G}}\) and \({\mathcal {G}}^{\mathbb {P}}\) is the completion of \({\mathcal {G}}\) under \({\mathbb {P}}\).
We then state Condition (A) from Nutz (2015).
Assumption 1
Let  , let τ be a stopping time such that τ≥s and \({\mathbb {P}}\in {\mathcal {P}}(s,\bar {\omega })\). Set \(\theta :=\tau ^{s,\bar {\omega }}-s\). (i) Measurability: The graph \(\{({\mathbb {P}}^{\prime },\omega):\; \omega \in \Omega, \; {\mathbb {P}}^{\prime }\in {\mathcal {P}}(\tau,\omega)\}\subseteq \mathfrak {P}(\Omega)\times \Omega \) is analytic. (ii) Invariance: We have \({\mathbb {P}}^{\theta,\omega }\in {\mathcal {P}}(\tau, \bar {\omega }\otimes _{s} \omega)\) for \({\mathbb {P}}\)-a.e ω∈Ω. (iii) Stability under pasting: If \(\nu :\Omega \to \mathfrak {P}(\Omega)\) is a \({\mathcal {F}}_{\theta }\)-measurable kernel and \(\nu (\omega)\in {\mathcal {P}}(\tau, \bar {\omega }\otimes _{s} \omega)\)for \({\mathbb {P}}\)-a.e ω∈Ω, then the measure defined by
, let τ be a stopping time such that τ≥s and \({\mathbb {P}}\in {\mathcal {P}}(s,\bar {\omega })\). Set \(\theta :=\tau ^{s,\bar {\omega }}-s\). (i) Measurability: The graph \(\{({\mathbb {P}}^{\prime },\omega):\; \omega \in \Omega, \; {\mathbb {P}}^{\prime }\in {\mathcal {P}}(\tau,\omega)\}\subseteq \mathfrak {P}(\Omega)\times \Omega \) is analytic. (ii) Invariance: We have \({\mathbb {P}}^{\theta,\omega }\in {\mathcal {P}}(\tau, \bar {\omega }\otimes _{s} \omega)\) for \({\mathbb {P}}\)-a.e ω∈Ω. (iii) Stability under pasting: If \(\nu :\Omega \to \mathfrak {P}(\Omega)\) is a \({\mathcal {F}}_{\theta }\)-measurable kernel and \(\nu (\omega)\in {\mathcal {P}}(\tau, \bar {\omega }\otimes _{s} \omega)\)for \({\mathbb {P}}\)-a.e ω∈Ω, then the measure defined by
is an element of \({\mathcal {P}}(s,\bar {\omega })\).
Exploiting the previous conditions, by Proposition 3.1 in Nutz (2015) we have the following
Theorem 1
Let σ≤τbe stopping times and  be an upper semianalytic functionFootnote 1. Then, under Assumption 1 the function
be an upper semianalytic functionFootnote 1. Then, under Assumption 1 the function
is \({\mathcal {F}}_{\tau }^{\ast }\)-measurable and upper semianalytic. Moreover,
Furthermore,
where \({\mathcal {P}}(\tau,{\mathbb {P}})=\{{\mathbb {P}}^{\prime }\in {\mathcal {P}}:\; {\mathbb {P}}^{\prime }={\mathbb {P}}\text {~on~} {\mathcal {F}}_{\tau }\}\), and in particular,
We finally call \({\mathcal {P}}\)-martingale or robust martingale, an adapted stochastic process M=(M s )s≥0 such that \({\mathcal {E}}_{0}(M_{t})\) is finite for every t and
for any T≥t. The particular \({\mathcal {P}}\)-martingales for which also (−M) is a \({\mathcal {P}}\)-martingale are called \({\mathcal {P}} \)-symmetric martingales.
We now provide another characterization of the conditional sublinear expectation given in (6). To this end, given an arbitrary \({\mathbb {P}}\in {\mathcal {P}}\) and a stopping time τ, we introduce the set
of the measures in \({\mathcal {P}}\) which are equivalent to \({\mathbb {P}}\) restricted to \({\mathcal {F}}_{\tau }\). In the case in which \({\mathcal {P}}\) is composed by local martingale measures relative to some price process S and every prior \({\mathbb {P}}\) describes a complete market model, it holds \({\mathcal {P}}_{\textup {eq}}(\tau,{\mathbb {P}})={\mathcal {P}}(\tau,{\mathbb {P}})\), but in general the inclusion in (8) is strict.
Proposition 1
Let τ be a stopping time and  an upper semianalytic function. Then under Assumption 1 for every \({\mathbb {P}}\in {\mathcal {P}}\) it holds
an upper semianalytic function. Then under Assumption 1 for every \({\mathbb {P}}\in {\mathcal {P}}\) it holds
Proof
It is sufficient to prove
as the reverse inequality is evident. Let for \({\mathbb {P}}\in {\mathcal {P}}\)
It follows from Theorem 1 that
is \({\mathcal {F}}_{\tau }^{\ast }\)-measurable, so that \(A^{\mathbb {P}}\in {\mathcal {F}}_{\tau }^{\ast }\subseteq {\mathcal {F}}_{\tau }^{\mathbb {P}}\). This implies that there exist \(F\in {\mathcal {F}}_{\tau }\) and \(N\in {\mathcal {N}}_{\tau }^{\mathbb {P}}\) (see Ash (1972) page 18), where
such that \(A^{\mathbb {P}}=F\cup N\) and for every \({\mathbb {Q}}\in {\mathcal {P}}_{\textup {eq}}(\tau,{\mathbb {P}})\)
This implies that for all \({\mathbb {Q}},{\mathbb {P}}^{\prime }\in {\mathcal {P}}_{\textup {eq}}(\tau,{\mathbb {P}})\)
Hence we have
because \({\mathcal {E}}_{\tau }(\xi)\) is defined ω per ω in (3), i.e. it is independent of the choice of \({\mathbb {Q}},{\mathbb {P}}^{\prime }\in {\mathcal {P}}_{\textup {eq}}(\tau,{\mathbb {P}})\). Inequality (9) holds for every \({\mathbb {Q}}\in {\mathcal {P}}_{\textup {eq}}(\tau,{\mathbb {P}})\), i.e. in particular for the initially chosen probability \({\mathbb {P}}\in {\mathcal {P}}\). □
Example 1
We illustrate the result of Proposition 1 in the case where the filtration is generated by a finite partition of Ω. In particular, we consider a toy model with time horizon T=2. Given a Polish space Ω, we set Ω
t
:=Ωt to be the t-fold Cartesian product of Ω for t∈{0,1,2} with the convention that Ω0 is a singleton. Let then \({\mathcal {F}}_{T}=\mathcal {B}(\Omega _{T})\) and \({\mathcal {F}}_{1}=\sigma (A_{1},\dots,A_{n})\), where (A
i
)i=1,…,n is a partition of Ω and  .
.
Similarly to Bouchard and Nutz (2015) we assume that for each t∈{0,1} and ω∈Ω t we have a nonempty set \({\mathcal {P}}_{t}(\omega):={\mathcal {P}}(t,\omega)\subseteq \mathfrak {P}(\Omega)\) of probability measures such that \({\mathcal {P}}_{t}\) admits a universally measurable kernel \({\mathbb {P}}_{t}\;:\;\Omega _{t}\to \mathfrak {P}(\Omega)\) with \({\mathbb {P}}_{t}(\omega)\in {\mathcal {P}}_{t}(\omega)\) for all ω∈Ω t . Therefore, we can consider a set of priors \({\mathcal {P}}\) for this two-period market such that for every \({\mathbb {P}}\in {\mathcal {P}}\) and \(A\in {\mathcal {F}}_{T}\) it holds that
where ω=(ω1,ω2) indicates a generic element in Ω T and \({\mathbb {P}}_{t}(\cdot)\in {\mathcal {P}}_{t}(\cdot)\), for t∈{0,1}. Alternatively stated, every \({\mathbb {P}}\in {\mathcal {P}}\) is of the type
for some \({\mathbb {P}}_{0}(\cdot)\in {\mathcal {P}}_{0}(\cdot)\) and \({\mathbb {P}}_{1}(\cdot)\in {\mathcal {P}}_{1}(\cdot)\).
Given a \({\mathcal {F}}_{T}\)-measurable function ξ and a prior \({\mathbb {P}}\in {\mathcal {P}}\), it holds that
Every term on the right side of (12) can be further rewritten as
where \(\xi _{{\mathbb {P}}_{1}}(\omega _{1}):=\int _{\Omega } \xi (\omega _{1},\omega _{2}){\mathbb {P}}_{1}(\omega _{1};d\omega _{2})\). As \(\xi _{{\mathbb {P}}_{1}}(\omega _{1})\) is constant on A i , we denote for simplicity \(\xi _{{\mathbb {P}}_{1}}(\omega _{1})=\xi _{{\mathbb {P}}_{1}}^{A_{i}}\) for ω1∈A i . It follows from (14) that
from which \(E_{\mathbb {P}}[\xi |{\mathcal {F}}_{1}]=\sum _{i=1}^{n} \xi _{{\mathbb {P}}_{1}}^{A_{i}} \textit {\textbf {1}}_{A_{i}}\). Because of (11), a probability \({\mathbb {P}}^{\prime }\in {\mathcal {P}}\)can be written as \({\mathbb {P}}^{\prime }={\mathbb {P}}^{\prime }_{0}\otimes {\mathbb {P}}^{\prime }_{1}\). This implies that, in order to have \({\mathbb {P}}^{\prime }\in {\mathcal {P}}(1,{\mathbb {P}})\), we must enforce a constraint for the component \({\mathbb {P}}^{\prime }_{0}\), while \({\mathbb {P}}^{\prime }_{1}\) is arbitrary. The same argument holds for \(\bar {{\mathbb {P}}}\in {\mathcal {P}}_{eq}(1,{\mathbb {P}})\). Hence it follows that
for all \({\mathbb {P}}\in {\mathcal {P}}\).
Finally we define the filtrations \({\mathbb {G}}=({\mathcal {G}}_{t})_{0\leq t\leq T}\), where
and \({\mathbb {G}}_{+}\), the smallest right-continuous filtration that contains \({\mathbb {G}}\).
Bubbles under uncertainty
Here, we begin our study of financial bubbles under model uncertainty.In order to be consistent with the classical literature, we consider a discounted risky asset given by a non-negative,  -valued, \({\mathbb {F}}^{\ast }\)-adapted, and \({\mathcal {P}}\)-q.s. continuous process S=(S
t
)t≥0. Let τ>0 q.s. be a stopping time describing the maturity of the risky asset and X
τ
be the final payoff or liquidation value at time τ. The bank account S0 is assumed to be constant and equal to 1. The wealth process W=(W
t
)t≥0 generated from owning the asset is given by
-valued, \({\mathbb {F}}^{\ast }\)-adapted, and \({\mathcal {P}}\)-q.s. continuous process S=(S
t
)t≥0. Let τ>0 q.s. be a stopping time describing the maturity of the risky asset and X
τ
be the final payoff or liquidation value at time τ. The bank account S0 is assumed to be constant and equal to 1. The wealth process W=(W
t
)t≥0 generated from owning the asset is given by
see alsoJarrow et al. (2007).
In the standard literature on bubbles it is usually assumed that the No Free Lunch With Vanishing Risk condition (NFLVR) holds. When working in the context of multiple priors models the situation becomes more involved. In fact, there does not yet exist a robust counterpart to NFLVR. There is actually just one well studied concept of arbitrage (arbitrage of the first kind (NA1)) in the continuous time setting under uncertainty introduced inBiagini et al. (2017). However inBiagini et al. (2017), the existence of absolutely continuous martingale measures requires introducing a stopping time ζ that causes a jump to a cemetery state, which is invisible under all \({\mathbb {P}}\in {\mathcal {P}}\) but may be finite under some \({\mathbb {Q}}\in \mathcal {Q}\), where \(\mathcal {Q}\) is an appropriate set of local martingale measures. Therefore, despite the possibility to start with a family \({\mathcal {P}}\) of physical measures, the results ofBiagini et al. (2017) require to reserve some particular care to the tractability of ζ. This is one of the reasons why, while working in the setting outlined, we assume the following for simplicity.
Assumption 2
We consider a family \({\mathcal {P}}\) of probability measures, possibly non dominated, satisfying Assumption 1 and such that the wealth process is a \({\mathbb {Q}}\)-local martingale for every \({\mathbb {Q}}\in {\mathcal {P}}\). Thus, the set \({\mathcal {P}}\) is made of local martingale measures, enforcing NFLVR under all \({\mathbb {Q}}\)-market.
By doing this we guarantee at the same time that W is justified by no arbitrage arguments under all probability scenarios.
In order to have a better understanding of what should be the right notion of asset fundamental value under model uncertainty, we first present a short survey on how this concept is modeled in the classical literature of financial bubbles.
For simplicity, we will start by considering a finite time horizon. Let then  be such that τ≤T. We note that in this case, W
t
=S
t
for every t∈[0,T], if X
τ
=S
τ
, which will be assumed throughout this section. Moreover, we assume S
T
to be measurable with respect to the Borel σ-field on Ω
T
, in order to be able to compute its conditional sublinear expectation.
be such that τ≤T. We note that in this case, W
t
=S
t
for every t∈[0,T], if X
τ
=S
τ
, which will be assumed throughout this section. Moreover, we assume S
T
to be measurable with respect to the Borel σ-field on Ω
T
, in order to be able to compute its conditional sublinear expectation.
Finally we conclude by providing some definitions by followingNutz (2015). We denote with \(L(S,{\mathcal {P}})\) the set of all  -valued, \({\mathbb {G}}\)-predictable processes H=(H
t
)t∈[0,T] such that the stochastic integral process \(\left (\int _{0}^{t} H_{s} dS_{s}\right)_{t\in [0,T]}\) is well-definedFootnote 2 for all \({\mathbb {P}}\in {\mathcal {P}}\).
-valued, \({\mathbb {G}}\)-predictable processes H=(H
t
)t∈[0,T] such that the stochastic integral process \(\left (\int _{0}^{t} H_{s} dS_{s}\right)_{t\in [0,T]}\) is well-definedFootnote 2 for all \({\mathbb {P}}\in {\mathcal {P}}\).
Definition 3
(seeNutz (2015), Section 3.2) We say that a \({\mathbb {G}}\)-predictable process \(H\in L(S,{\mathcal {P}})\) is admissible if \(\left (\int _{0}^{t} H_{s} dS_{s}\right)_{t\in [0,T]}\) is a \({\mathbb {P}}\)-supermartingale for every \({\mathbb {P}}\in {\mathcal {P}}\). We denote by \(\mathcal {H}\) the set of all admissible processes.
Classical setting for bubble modeling
In the classical setting the elements of \({\mathcal {P}}\) are assumed to be all equivalent to a probability measure \(\mathbb {P}\), i.e., \({\mathcal {P}}= \mathcal {M}_{loc}(S)\), where \(\mathcal {M}_{loc}(S)\) denotes the set of the equivalent local martingale measures for S. Under this assumption there are two main approaches for defining the fundamental value of a financial asset. In the setting ofBiagini et al. (2014);Jarrow et al. (2007), andJarrow et al. (2010), the fundamental value is defined as the asset’s discounted future payoffs under a risk neutral measure. This means that if \(\mathbb {Q}\in \mathcal {M}_{loc}(S)\), the fundamental value \(S^{\ast,{\mathbb {Q}}}=\left (S^{\ast,{\mathbb {Q}}}_{t}\right)_{t\in [0,T]}\) under \({\mathbb {Q}}\) is given by
for every t∈[0,T], where T is a fixed finite time horizon. For any \(\mathbb {Q}\in \mathcal {M}_{loc}(S)\) the non-negative process
is called the \(\mathbb {Q}\)-bubble. The concept of bubble depends on the following distinction
where \(\mathcal {M}_{UI}(S)\) is the class of measures \({\mathbb {Q}}\approx {\mathbb {P}}\) such that S is a uniformly integrable martingale under \({\mathbb {Q}}\) and \(\mathcal {M}_{NUI}(S)=\mathcal {M}_{loc}(S)\setminus \mathcal {M}_{UI}(S)\).
The market bubbliness thus is built upon the investor’s views: if she acts accordingly to a \(\mathbb {Q}\in \mathcal {M}_{UI}(W)\), then she would see no bubble; on the contrary, if \(\mathbb {Q}\in \mathcal {M}_{NUI}(W)\) is perceived to be the right market view, then there would be an asset bubble. In this sense, the concept of bubble is dynamic: bubbles are born or burst depending on how the investor changes her perspectives on the market.
If the market is complete the situation simplifies. As \(\mathcal {M}_{loc}(S)\) is made of a unique element (and it must exist if the usual NFLVR condition holds), either there is a bubble from the beginning or there is no bubble at all. This result agrees with the second main approach to financial bubbles (seeHerdegen and Schweizer (2016) and the references therein), in which the fundamental value coincides with the superreplication price. Denoting by \(\mathbb {L}^{0}_{+}({\mathcal {F}}_{t})\) the set of \({\mathcal {F}}_{T}\)-measurable random variables taking \({\mathbb {P}}\)-a.s. values in [0,∞), the superreplication price is given by
for t∈[0,T] and Θ denoting the class of \({\mathbb {F}}\)-predictable and S-integrable processes. Given the duality (see Kramkov1996)
where the essential supremum of the family of random variables \(E_{\mathbb {Q}}[S_{T}|{\mathcal {F}}_{t}]\), \({\mathbb {Q}}\in \mathcal {M}_{loc}(S)\), is taken under \({\mathbb {P}}\), if there exists a bubble in a complete market, then the superreplication price must be lower than the actual price of the asset observed in the market.
Differences between the two approaches emerge in the context of incomplete markets. Given the superreplication duality (16), as soon as \(\mathcal {M}_{UI}(S)\neq \emptyset \), then there is no bubble. The concepts of bubble itself and bubble birth change. It might be that the superreplication price and the market price are equal at t=0, but they may differ at a later time t>0 (see Example 3.7 inHerdegen and Schweizer (2016)): at time t is the bubble is born. Here the “bubble misprice” on an asset is given by the fact that we can get the same wealth at the end, but by exploiting an investment strategy with a lower initial price. Still, we cannot profit from this opportunity because its generating strategy is not admissible: we need to go short on the asset and long on the superreplicating strategy to generate a sure profit at terminal time but by doing this we also face the risk of unbounded losses in (0,T). In this setting, if a bubble exists then it is perceived by any investor, independently from the particular choice of the pricing measure \({\mathbb {Q}}\in \mathcal {M}_{loc}(S)\).
Finally, we present an interesting result that links the two settings described above. We prove that if there is no \({\mathbb {Q}}\in \mathcal {M}_{loc}(S)\) that excludes the presence of a bubble in the sense ofBiagini et al. (2014) orJarrow et al. (2010), then there is also a bubble in the case when fundamental values are given by superreplication prices.
Proposition 2
Let S=(S t )t∈[0,T] be a continuous, non-negative, adapted process in a filtered probability space \((\Omega, {\mathcal {F}}, {\mathbb {F}}, {\mathbb {P}})\), where the filtration \({\mathbb {F}}=({\mathcal {F}}_{t})_{t\in [0,T]}\) satisfies the usual conditions. If \(\mathcal {M}_{loc}(S)=\mathcal {M}_{NUI}(S)\), then there is a t∈[0,T)such that with positive probability
Proof
We argue by contradiction. If we suppose that
for every t∈[0,T], the process π(S) defined in (16) is a \({\mathbb {Q}}\)-local martingale for each \({\mathbb {Q}}\in \mathcal {M}_{loc}(S)\). This implies, according to Theorem 3.1 inKramkov (1996), that the minimal superreplicating portfolio V=(V t )t∈[0,T], where
and H is a predictable, S-integrable process, is non-negative, and self-financing and thus that there exists \(\bar {{\mathbb {Q}}}\in \mathcal {M}_{loc}(S)\cap \mathcal {M}_{UI}(S)\) (see Kramkov1996, Section 3.2), contradicting the hypothesis. □
Remark 1
It is also possible to obtain the same result when, instead of considering \(\mathcal {M}_{loc}(S)\), we look at
In this context, if \({\mathcal {P}}\) is m-stableFootnote 3, it is possible to define the asset fundamental value as
for any t∈[0,T] (for this result we refer toDelbaen (2006)). As the measures in \({\mathcal {P}}\) which are equivalent to \({\mathbb {P}}\) are dense in \({\mathcal {P}}\) (see againDelbaen (2006)), it holds
so that Proposition 2 also applies in this case.
Robust fundamental value
We start this section with a discussion on suitable requirements for defining a bubble under uncertainty. We note that when \({\mathcal {P}}=\mathcal {M}_{loc}(S)\), the model should collapse into one of the two approaches mentioned in the previous section. This already tells us that the fundamental value under uncertainty should be defined in terms of some conditional expectation.
A first attempt would be to define the existence of an asset bubble when there exists a \(\mathbb {Q}\)-bubble for at least one \({\mathbb {Q}}\in {\mathcal {P}}\) in the classical sense of “Classical setting for bubble modeling” section. However, this would imply that any classical bubble will turn into a bubble under uncertainty. To overcome this problem, it is crucial to introduce a meaningful concept for the fundamental value \(S^{\ast }=(S^{\ast }_{t})_{t\in [0,T]}\) under uncertainty. We could set
for each \({\mathbb {Q}}\in {\mathcal {P}}\). In this way we would be consistent with the existing literature and recover the traditional setup ofJarrow et al. (2010) when \({\mathcal {P}}\) consists of only one probability measure. This class of \(\mathbb {Q}\)-fundamental values cannot eventually be aggregated (this is already the case with the G-setting, see Soner et al.2011a). In this setting, we could define a bubble as the situation in which
for each \(\mathbb {Q}\in {\mathcal {P}}\) and some t>0. Alternatively stated, we would say that the asset S is a \({\mathcal {P}}\)-bubble if it is a \(\mathbb {Q}\)-bubble for every \(\mathbb {Q}\in {\mathcal {P}}\). However, this seems to be too strong of a requirement.
There is also a deeper issue, which is peculiar to the nature of our framework. In a market model that is intrinsically incomplete, it is not immediate to transpose the concept of “risk neutral expectation of future discounted payoffs” from the classical setting to the modeling under uncertainty, because of the absence of a linear pricing system. We refer toBeissner (2012) for a discussion on linear pricing systems and the fundamental theorem in the context of uncertain volatility. For a thorough analysis on the foundations of financial economics under Knightian Uncertainty, see alsoBurzoni et al. (2017). The first naive definition of fundamental value under uncertainty that we propose above is actually linked to this notion, as it coincides with the approach ofJarrow et al. (2010) when \({\mathcal {P}}\) reduces to a singleton.
Definition 4
We call robust fundamental value the process \(S^{\ast }=(S_{t}^{\ast })_{t\in [0,T]}\), where
for every \(\mathbb {Q}\in {\mathcal {P}}\), with \(\mathcal {P}(t,\mathbb {Q})=\{{\mathbb {Q}}^{\prime }\in {\mathcal {P}}:\;\mathbb {Q}^{\prime }=\mathbb {Q} \text {~on~} \mathcal {F}_{t}\}\).
Theorem 1, Proposition 1, and Theorem 4 play a fundamental role in our specification of the robust fundamental value. Definition 4 is motivated by the intuition that in presence of uncertainty we should consider a maximal fundamental value, taking in account of each fundamental value under the different priors. This can be only achieved if aggregation of the conditional expectations is possible, which is guaranteed by the results of Theorem 1. Furthermore, Theorem 1 ensures that the resulting robust fundamental value is sub-linear, which extends the classical concept of linear pricing operator. This sublinearity property plays a fundamental role in allowing an arbitrage-free setting, see againBeissner (2012) andBurzoni et al. (2017). We then obtain by Proposition 1 that the aggregation can be done on the set of priors having the same family of null sets up to time t, i.e. sharing the same view on the “impossible" events up to time t. This result extends Theorem 1, where aggregation is done on the set of probability measures coinciding up to time t, i.e. exactly sharing the same view on all measurable sets up to time t. A financial interpretation and a link to the classical literature on bubble is then provided by Theorem 4, which shows when S∗ coincides with the superreplication value.
This is the case in the G-expectation framework. The same holds true for \(S^{\ast }_{0}\) or when the sublinear operator is right-continuous, see for example Theorem 8, if the family \({\mathcal {P}}\) is saturated.
Definition 5
(see Nutz2015, Section 2) A set \({\mathcal {P}}\) of probability measures on \((\Omega,{\mathcal {F}})\) is called saturated if the following condition is satisfied: for all \({\mathbb {P}}\in {\mathcal {P}}\), if \({\mathbb {Q}}\) is a sigma-martingale measure for S equivalent to \({\mathbb {P}}\), then \({\mathbb {Q}}\in {\mathcal {P}}\).
If the family \({\mathcal {P}}\) is saturated, we have that by Theorem 3.2 inNutz (2015)

see also Appendix for further details. In this way our approach extends in a natural way the setting ofHerdegen and Schweizer (2016) to the case of mutually singular priors.
Furthermore we also have a strong link to the literature in the classical case, as we show in the following proposition.
Proposition 3
Let \({\mathcal {P}}={\mathcal {M}_{loc}}(S)\), then the robust fundamental value (19) coincides with the classical superreplication price, i.e.,
where \({\mathcal {M}_{loc}}(S,t,{\mathbb {Q}}):=\{{\mathbb {Q}}^{\prime }\in {\mathcal {M}_{loc}}(S)\;|\; {\mathbb {Q}}^{\prime }={\mathbb {Q}} \text {~on~} {\mathcal {F}}_{t}\}\).
Proof
We prove that
for every \({\mathbb {Q}}^{1}, {\mathbb {Q}}^{2}\in {\mathcal {M}_{loc}}(S)\) by a measure pasting argument similar to Proposition 9.1 inDelbaen (2006). This suffices to conclude as
but (21) also guarantees
Assume \({\mathbb {Q}}^{2}\in {\mathcal {M}_{loc}}(S)\setminus {\mathcal {M}_{loc}}(t,{\mathbb {Q}}^{1})\), otherwise the claim is trivial. We note that
for every \({\mathbb {Q}}\in {\mathcal {M}_{loc}}\left (S,t,{\mathbb {Q}}^{i}\right)\), i=1,2. This is clear as, for every \(A\in {\mathcal {F}}_{T}\), it must hold
Now, define
which is the Radon-Nykodim derivative of an ELMM, as proven in Proposition 9.1 inDelbaen (2006). The measure \({\mathbb {Q}}^{\prime }\) associated to (Z s )s∈[0,T] thus belongs to \({\mathcal {M}_{loc}}(S,t,{\mathbb {Q}}^{1})\) and satisfies
This shows that for every \({\mathbb {Q}}\in {\mathcal {M}_{loc}}\left (S,t,{\mathbb {Q}}^{2}\right)\) there exists a \({\mathbb {Q}}^{\prime }\in {\mathcal {M}_{loc}}\left (S,t,{\mathbb {Q}}^{1}\right)\) such that \(E_{{\mathbb {Q}}^{\prime }}[S_{T}|{\mathcal {F}}_{t}]= E_{{\mathbb {Q}}}[S_{T}|{\mathcal {F}}_{t}]\). This is enough to establish (21). □
Remark 2
Note that in Proposition 3 we can consider quasi-sure equalities as \({\mathcal {P}}={\mathcal {M}_{loc}}(S)\).
We now introduce the notion of bubble in this setting.
Definition 6
The asset price bubble β=(β t )t∈[0,T] for S is given by
where S∗ is defined in (19).
It then follows that the asset price bubble is different from zero if there exists a stopping time τ such that
for a \({\mathbb {Q}}\in {\mathcal {P}}\). It is not necessary to have a bubble under all scenarios to have a bubble under uncertainty. The parallel with the notion of robust arbitrage now becomes evident. As S is a non-negative \({\mathbb {Q}}\)-local martingale, hence a \({\mathbb {Q}}\)-supermartingale, we have
for every t∈[0,T] and \({\mathbb {Q}}\in {\mathcal {P}}\). There is now a bubble in the market at a stopping time τ if there exists a scenario (a probability measure \(\bar {{\mathbb {Q}}}\in {\mathcal {P}}\)) such that the robust fundamental value is smaller than the market value with positive probability and all probabilities that coincide with \(\bar {{\mathbb {Q}}}\) on \({\mathcal {F}}_{\tau }\) agree on this view. In the case of no duality gap, our definition of bubble extends the approach where fundamental prices are given by superreplication prices as inHerdegen and Schweizer (2016) to the framework under uncertainty.
Saturation, as from Definition 5, however, is a condition that we do not enforce on our model, but which is automatically satisfied if every \({\mathbb {Q}}\)-market is complete. In all other cases the occurrence of a bubble may be caused either by a difference between the market price and the superreplication price or by a duality gap in

This second situation is precisely the one considered inCox et al. (2016) in order to detect a bubble. This means that S∗ can always be viewed at least as the worst model price, among the models considered by the investor.
Properties and examples
Lemma 1
The bubble β is a non-negative \({\mathbb {Q}}\)-local submartingale for every \({\mathbb {Q}}\in {\mathcal {P}}\), such that β T =0 q.s. Moreover, if there exists a bubble, S is not a \({\mathcal {P}}\)-martingale.
Proof
This immediately follows from Definition 4, as β is the difference between a \({\mathbb {Q}}\)-local martingale and a \({\mathbb {Q}}\)-supermartingale. □
The local submartingale characterization is not at all a contradiction as it may seem at first sight. In fact, as opposed to non-negative local supermartingales, non-negative local submartingales do not have to be true submartingales. There are a variety of examples of local submartingales with nonstandard behavior, such as decreasing mean, as shown inElworthy et al. (1999) andPal and Protter (2010). To mention a clear example, it suffices to consider the class of non-negative local martingales: such processes are non-negative local submartingale and also supermartingales.
We present an example of a bubble by adapting one result ofCox and Hobson (2005) to the context of G-expectation.
Remark 3
We highlight that in Example 2, 3, and 4 the asset price S is a \({\mathbb {Q}}\)-local martingale for every \({\mathbb {Q}}\in {\mathcal {P}}\)under the completed filtration \({\mathbb {F}}^{\mathbb {Q}}=\left \{{\mathcal {F}}_{t}^{\mathbb {Q}}\right \}_{t\geq 0}\). However, being a non-negative process adapted to \({\mathbb {F}}^{\ast }\subseteq {\mathbb {F}}^{\mathbb {Q}}\), S is also a \({\mathbb {Q}}\)-local martingale with respect to the filtration \({\mathbb {F}}^{\ast }\), thanks to a result from (Stricker 1977) that we report in the formulation of Theorem 10 from Föllmer and Protter (2011).
Theorem 2
Let X be a non-negative local martingale for \({\mathbb {G}}\) and assume that X is adapted to the subfiltration \({\mathbb {F}}\subseteq {\mathbb {G}}\). Then, X is also a local martingale for \({\mathbb {F}}\).
Example 2
Let \({\mathcal {P}}= {\mathcal {P}}_{\textbf {D}}\) as in Proposition 7, where  . Let S0=s>0 and
. Let S0=s>0 and
The process in (23) is well defined for any t∈[0,T−ε], for ε>0, as a consequence of the results of Luo and Wang (2014). We show that S is a price process with a bubble by showing that S is a non-negative \({\mathbb {Q}}\)-local martingale for every \({\mathbb {Q}}\in {\mathcal {P}}\), with terminal value equal to zero. To this purpose, let us fix a prior \({\mathbb {Q}}\). We have that
The stochastic integral \(\int _{0}^{\cdot } 1/ \sqrt {T-s} dB_{s}\) is a \({\mathbb {Q}}\)-local martingale on [0,T), such that the quadratic covariation is
and continuous on [0,T). Using the same argument as in Lemma 5 from Jarrow et al. (2007), which exploits the Dubins-Schwarz theorem together with the law of the iterated logarithm, we can argue that
Hence, we set S T =0 so that S is q.s. continuous on [0,T]. This follows as the set \(\{\omega \in \Omega :\;{\lim }_{u\to T}S_{u}\neq 0\}\) is polar: the existence of \({\mathbb {Q}}\in {\mathcal {P}}\) such that \({\mathbb {Q}}({\lim }_{u\to T}S_{u}\neq 0)>0\) is in fact in contradiction with (24). Hence, S is not a \({\mathbb {Q}}\)-martingale for any \({\mathbb {Q}}\in {\mathcal {P}}\) as \(E_{\mathbb {Q}}[S_{T}]=0<E_{\mathbb {Q}}[S_{0}]\), and in particular it is not a robust martingale.
Another example comes from adapting the concept of the Bessel process to the context of model uncertainty.
Example 3
We consider \({\mathcal {P}}={\mathcal {P}}_{\textbf {D}}\), where  consists of the matrices (ai,j)i,j=1,2,3 such that ai,j=0 for all i≠j, a1,1=a2,2=a3,3∈[1,2] in order to fix some values.
consists of the matrices (ai,j)i,j=1,2,3 such that ai,j=0 for all i≠j, a1,1=a2,2=a3,3∈[1,2] in order to fix some values.
Let \(\mathbf {B}=(\mathbf {B}_{t})_{t\in [0,T]}=\left (B_{t}^{1},B_{t}^{2},B_{t}^{3}\right)_{t\in [0,T]}\). We consider the process given by f(B)=(f(B t ))t∈[0,T], where B0=(1,0,0) and f(x)=∥x∥−1. As f is Borel-measurable, we can compute the sublinear expectation \({\mathcal {E}}_{0}(f(\mathbf {B}_{t}))\) for any t∈[0,T], according to Theorem 1. It is a well known result that f(B) is a strict \({\mathbb {Q}}\)-local martingale for all \({\mathbb {Q}}\in {\mathcal {P}}_{\textbf {D}}\) (see for example Revuz and Yor 1999, Exercise XI.1.16). To prove that the price process has a bubble, it suffices to show that f(B) is not a \({\mathcal {P}}_{\textbf {D}}\)-martingale. This can be done using an argument from Föllmer and Protter (2011), where the inverse three-dimensional Bessel process is projected on the filtration generated by the first component of the Brownian motion. Theorem 14 from Föllmer and Protter (2011) in particular proves that
where Φ is the cumulative distribution function of a standard normal random variable. Using the invariance by rotation of the Brownian motion it is possible to show that, for Wσ=σB where  and W now issued at a generic point
and W now issued at a generic point  , the equality (25) generalizes to
, the equality (25) generalizes to
Let us now consider a prior \({\mathbb {Q}}\in {\mathcal {P}}_{\textbf {D}}\) and a sequence Bn of processes such that
and \(\textbf {B}^{n}_{t_{i}}-\textbf {B}^{n}_{t_{i-1}}\sim N\left ({0},(t_{i}-t_{i-1})\boldsymbol {\sigma }_{t_{i-1}}^{2}\right)\), where \(t_{i}=\frac {Ti}{n}\) and \(\boldsymbol {\sigma }_{t_{i-1}}\) is a D-valued, \({\mathcal {F}}_{t_{i-1}}\)-measurable function. We can now compute
where \([\boldsymbol {\sigma }_{t_{n-1}}]_{11}\) stands for the first entry of the diagonal matrix \(\boldsymbol {\sigma }_{t_{n-1}}\) whose elements different from zero are all equal and \(\tilde {\mathbf {B}}^{n}\) is the process where \(\boldsymbol {\sigma }_{t_{n-1}}\) is replaced by the identity matrix in  . We can iterate the previous computation by noting that
. We can iterate the previous computation by noting that
After n iterations we finally obtain
We can use this result to show that
thus proving that f(B)is not a robust martingale. If we denote with  a sequence of bounded and continuous functions converging increasingly to f, the convergence (27) ensures that
a sequence of bounded and continuous functions converging increasingly to f, the convergence (27) ensures that
On the other hand, as f dominates fm and because of (28), \(E_{\mathbb {Q}}\left [\frac {1}{f^{m}(\mathbf {B}_{T})}\right ]< c\), with 0<c<1, for m big enough. It is then possible to use monotone convergence to prove
As this holds for every \({\mathbb {Q}} \in {\mathcal {P}}_{\textbf {D}}\), we obtain (29).
In both Example 2 and 3, the risky asset is a strict \({\mathbb {Q}}\)-local martingale for every \({\mathbb {Q}}\in {\mathcal {P}}\). This means that the bubble in those cases is perceived under all priors which are possible in the model.
By slightly modifying the framework of Example 3, we are able to obtain a bubble that is a \(\bar {{\mathbb {Q}}}\)-martingale for a particular \(\bar {{\mathbb {Q}}}\in {\mathcal {P}}\). Thus, despite the existence of a bubble, an investor endowed only with the prior \(\bar {{\mathbb {Q}}}\) would not detect it. This is one of the main novelties of our model: when a bubble arises it will be identified by an agent whose significative sets are those with positive probability under any \({\mathbb {Q}}\in {\mathcal {P}}\); alternatively stated, this agent considers negligible only the polar sets, i.e., those \(A\in {\mathcal {F}}\) such that \({\mathbb {Q}}(A)=0\) for all \({\mathbb {Q}}\in {\mathcal {P}}\). However, an investor affected by less uncertainty, who neglects only the \(\bar {{\mathbb {Q}}}\)-null sets, will not spot the bubble.
Example 4
We consider \({\mathcal {P}}={\mathcal {P}}_{\textbf {D}}\) as in Example 3, but now we choose D in a way to allow for a degenerate case, where there exists \(\bar {Q}\in {\mathcal {P}}\) such that the canonical process is constantly equal to its initial value. We do this by considering the same setup as in Example 3, but choosing a1,1=a2,2=a3,3∈[0,2]. Exactly as in Example 3, f(B) is a \({\mathbb {Q}}\)-local martingale for every \({\mathbb {Q}}\in {\mathcal {P}}\). However, under the “degenerate prior” \(\bar {{\mathbb {Q}}}\), associated to a volatility constantly equal to 0, every process turns deterministic. This implies in particular that \(f(\mathbf {B}_{t})=f(\mathbf {B}_{0})=1 \bar {{\mathbb {Q}}}\)-a.s. for every t∈[0,T], which in turn ensures that f(B) is a true \(\bar {{\mathbb {Q}}}\)-martingale, while being a strict \({\mathbb {Q}}\)-local martingale for all \({\mathbb {Q}}\in {\mathcal {P}}\setminus \{\bar {{\mathbb {Q}}}\}\).
The examples regarding financial bubbles are usually obtained by showing specific asset dynamics with strict local martingale behavior. We give here an example of a bubble in uncertainty setting by focusing our attention on the choice of probability measures considered in the uncertainty framework.
Example 5
We adopt here the financial model introduced in Nutz and Soner (2012). The major difference with respect to the setting presented in “The setting” section is that we consider the set \({\mathcal {P}}_{S}\) of laws
In (30), \({\mathbb {Q}}_{0}\) denotes the Wiener measure, while αranges over all the \({\mathbb {F}}\)-progressively measurable processes with values in \(\mathbb {S}_{d}^{+}\) satisfying \(\int _{0}^{T} |\alpha _{s}| ds<\infty {\mathbb {Q}}_{0}\)-a.s. Here  represents the set of all strictly positive definite matrices and the stochastic integral in (30) is the Itô integral under \({\mathbb {Q}}_{0}\). The set \({\mathcal {P}}\) is asked to be stable under pasting, according to the following definition.
represents the set of all strictly positive definite matrices and the stochastic integral in (30) is the Itô integral under \({\mathbb {Q}}_{0}\). The set \({\mathcal {P}}\) is asked to be stable under pasting, according to the following definition.
Definition 7
The set \({\mathcal {P}}\)is stable under \({\mathbb {F}}\)-pasting if for all \({\mathbb {Q}}\in {\mathcal {P}}\), σ stopping time taking finitely many values, \(\Lambda \in {\mathcal {F}}_{\sigma }\) and \({\mathbb {Q}}_{1},{\mathbb {Q}}_{2}\in {\mathcal {P}}(\sigma, {\mathbb {Q}})\), the measure \(\bar {{\mathbb {Q}}}\) defined by
is again an element of \({\mathcal {P}}\).
Otherwise we leave all the other definitions stated in the preceding sections unchanged. Consider a risky asset S such that there exists a \({\mathbb {Q}}^{\tilde {\alpha }}\in {\mathcal {P}}_{S}\) for which the asset is a strict \({\mathbb {Q}}^{\tilde {\alpha }}\)-local martingale. For example, we can take S to be the process described in Example 2. We then study how a bubble is generated in this model. To this purpose we consider a subset \({\mathcal {P}}\subseteq {\mathcal {P}}_{S}\) given by those \({\mathbb {Q}}^{\alpha }\in {\mathcal {P}}_{S}\) for which
for some t∈(0,T). With such requirement, the set \({\mathcal {P}}\) is stable under pasting, according to Definition 7, thanks to the same proof of Lemma 3.3 in Nutz and Soner (2012). In other words, we are considering a subset of \({\mathcal {P}}_{S}\) where there is no uncertainty after time t, and where the volatility on (t,T] implies a strict local martingale behavior under at least one prior. It follows that, for every s>t,
thus implying the presence of a bubble.
We now investigate another interesting relation between robust and classical bubbles. The arguments in “Robust fundamental value” section clarified that the existence of \({\mathbb {Q}}\in {\mathcal {P}}\) and t∈[0,T) such that
implies the presence of a bubble in the classical sense for all the \({\mathbb {Q}}^{\prime }\)-markets with \({\mathbb {Q}}^{\prime }\in {\mathcal {P}}(t,{\mathbb {Q}})\). This is evident for at least two situations: when every \({\mathbb {Q}}\)-market admits a unique ELMM or when fundamental prices are described as the expected value of future discounted payoffs. However, we now show that the reverse is not true, i.e., the presence of a bubble with respect to some \({\mathbb {Q}}\in {\mathcal {P}}\) does not determine the existence of a bubble under uncertainty. We do that by showing that set of priors \({\mathbb {Q}}\in {\mathcal {P}}\) for which S is a strict local martingale cannot be a singleton. To show this result we consider the setting outlined in Example 5. This choice allows at the same time to ease the computations as well as to infer some conclusions about the framework outlined in “The setting” section, as both models can describe the G-setting.
Proposition 4
Consider the financial model introduced in Example 5. If \(\bar {{\mathbb {Q}}}\) is the pasting of \({\mathbb {Q}}\), \({\mathbb {Q}}_{1}\), and \({\mathbb {Q}}_{2}\) at the stopping time σ and \(\Lambda \in {\mathcal {F}}_{\sigma }\), as in (31), it holds that
for any positive \({\mathcal {F}}_{T}\)-measurable random variable Y and stopping time τ such that τ(ω)≤σ(ω) for every ω∈Ω.
Proof
We follow a procedure similar to Lemma 6.40 inFöllmer and Schied (2011) to prove (32). Let τ be a stopping time and Y a positive \({\mathcal {F}}_{T}\)-measurable random variable. By (31) we have that
so that, for every positive \({\mathcal {F}}_{\tau }\)-measurable random variable φ, we can study the value of
The expectation in (33) can then be written as
Hence, we can conclude that if τ≤σ the equality (32) holds. □
No dominance
In this section, we investigate the implications of no dominance in our market model. This as a concept first appeared inMerton (1973). It is natural to transpose this concept to our setting with uncertainty, as we do in the following definition.
Definition 8
Consider a market model under a set of priors \({\mathcal {P}}\). The i-th security Si is undominated on [0,T] if there is no admissible strategy \(H\in {\mathcal {H}}\) such that
and there exists a \({\mathbb {Q}}\in {\mathcal {P}}\)such that
A market satisfies robust no dominance (RND) on [0,T] if each Si, i∈{1,…,d}, is undominated on [0,T].
Definition 8 coincides with Definition 2 ofJarrow and Larsson (2012) for the classical situation in which a unique prior \({\mathbb {Q}}\) exists.
Remark 4
It is important to note that, as in the classical case, if Si is undominated on [0,T], it also undominated on [0,T′], for T′<T. Let Hi be given by
with 1 in position i. The trading strategy Hi is admissible, being Si a \({\mathbb {Q}}\)-local martingale for every \({\mathbb {Q}}\in {\mathcal {P}}\). If there would be a dominating strategy H on [0,T′], by applying the strategy \(\phantom {\dot {i}\!}K=H{\mathbf {1}}_{\{{t\leq T^{\prime }}\}} + H^{i}{\mathbf {1}}_{\{{t>T^{\prime }}\}}\), we would obtain
together with the existence of a \({\mathbb {Q}}\in {\mathcal {P}}\)such that
The ND assumption plays a key role in the classical literature on bubbles. We just mention two results by recalling that, if enforced, this concept rules out bubbles in the complete market models described byJarrow et al. (2007); moreover, ND is precisely the ingredient needed to exclude bubbles in the setting ofHerdegen and Schweizer (2016), where fundamental values are modeled with superreplication prices. Similar results can also be obtained in the present framework.
Lemma 2
Suppose that for each \({\mathbb {Q}}\in {\mathcal {P}}\) the \({\mathbb {Q}}\)-market model is complete. If robust no dominance holds, then there exists no bubble.
Proof
Observe that, if each \({\mathbb {Q}}\)-market is complete, the results ofNutz (2015) guarantee the duality

In the presence of a bubble, the superreplicating strategy would then dominate S, in contradiction with RND. □
Hence, in the general case, under RND any bubble would be the result of a duality gap in (??), which is the case considered inCox et al. (2016).
We remark how in general RND does not imply NFLVR for every \({\mathbb {Q}}\)-market, \({\mathbb {Q}}\in {\mathcal {P}}\). It is in fact well known that ND is stronger than NFLVR in the single prior setting, but it is a priori not necessary that RND implies ND for every \({\mathbb {Q}}\)-market.
Infinite time horizon
Here we study the case of an infinite time horizon. This is done for the sake of completeness, since we prove that in this context bubbles under uncertainty can be robust martingales. Let τ>0 q.s. be a stopping time describing the maturity of the risky asset. To reflect the impossibility for the investor to consume the final payoff of S in the case {τ=∞}, we generalize the definition of robust fundamental value established in (19) by setting
for every t≥0 and \({\mathbb {Q}}\in {\mathcal {P}}\). The fundamental value (36) includes the finite time horizon case (19) and is well defined, as shown in the following proposition.
Proposition 5
The fundamental value (36) is well defined. In addition, St∧τ converges to S τ q.s. for t→∞.
Proof
Fixed \({\mathbb {Q}}\in {\mathcal {P}}\), we know that W t :=St∧τ, t≥0, is a \({\mathbb {Q}}\)-supermartingale, which then converges \({\mathbb {Q}}\)-a.s. to S τ for t→∞, because of the classical supermartingale convergence theorem (see Dellacherie et al.1982, V.28 and VI.6). Therefore, St∧τ→S τ q.s., thanks to the same argument used in Example 2, and S τ is Borel measurable. Hence, S τ 1{τ<∞} is a Borel measurable random variable and we can compute its sublinear conditional expectation. Moreover, as W is a robust supermartingale, by Fatou’s Lemma we obtain
which guarantees \({\mathcal {E}}_{0}(S_{\tau }{\mathbf {1}}_{\{{\tau <\infty }\}})<\infty \). □
We also introduce the notion of robust fundamental wealth, by defining the process \(W^{\ast }=(W^{\ast }_{t})_{t\geq 0}\), where
for all \({\mathbb {Q}}\in {\mathcal {P}}\). A bubble is defined as in the finite time horizon case, i.e.,
for every t≥0. As a consequence, the case τ=∞ q.s. implies the presence of a bubble under uncertainty. As argued inJarrow et al. (2007), the bubble appearing in this situation is analogous to fiat money, a terminal value obtained at ∞. We report here Example 2 fromJarrow et al. (2007) to clarify this point.
Example 6
Let S
t
=1 for all  be fiat money. Since money never matures, we have τ=∞, S
τ
=1 and \(S_{t}^{\ast }=0\) q.s. for all t≥0. As
be fiat money. Since money never matures, we have τ=∞, S
τ
=1 and \(S_{t}^{\ast }=0\) q.s. for all t≥0. As
this means that the entire value of the asset comes from the bubble.
We summarize these results in the following proposition.
Proposition 6
It holds: (i) In the case there exists a \(\bar {{\mathbb {Q}}}\in {\mathcal {P}}\) and t≥0 such that \(\bar {{\mathbb {Q}}}^{\prime }(\tau =\infty)=1\) for all \(\bar {{\mathbb {Q}}}^{\prime }\in {\mathcal {P}}(t,\bar {{\mathbb {Q}}})\), there exists a bubble. (ii) The bubble β is a \({\mathbb {Q}}\)-local submartingale for every \({\mathbb {Q}}\in {\mathcal {P}}\). (iii) The wealth process W can be a \({\mathcal {P}}\)-symmetric martingale also in the presence of a bubble.
Proof
The proof of (i) follows from (37), noting that
as by hypothesis
for all \(\bar {{\mathbb {Q}}}^{\prime }\in {\mathcal {P}}(t,\bar {{\mathbb {Q}}})\). The local submartingale property follows from the definition of bubble and from Assumption 2. The wealth process can be a \({\mathcal {P}}\)-symmetric martingale as it can be seen in Example 6. □
Appendix
Superhedging duality
In the framework of “The setting” section, we now study the problem of robust superreplication of a contingent claim in a dynamical setting. The following results are of independent interest, but they also play an important role for studying financial bubbles under model uncertainty, as explained in “Robust fundamental value” section. We consider, as done inNutz (2015), an asset price process S which is  -valued, \({\mathbb {G}}_{+}\)-adapted with càdlàg paths. We first present a brief recap regarding the duality result proved inNutz (2015).
-valued, \({\mathbb {G}}_{+}\)-adapted with càdlàg paths. We first present a brief recap regarding the duality result proved inNutz (2015).
By Theorem 3.2 inNutz (2015) we have that, if the set \({\mathcal {P}}\) is saturated

where f is an upper semianalytic, \({\mathcal {G}}_{T}\)-measurable function such that \({\mathcal {E}}_{0}(|f|)<\infty \).
We begin by introducing some notations.
Definition 9
A real-valued, \({\mathbb {F}}\)-adapted process with càdlàg paths is called \({\mathcal {P}}\)-local supermartingale if it is a local supermartingale with respect to \(\left ({\mathbb {P}},{\mathbb {F}}_{+}^{\mathbb {P}}\right)\) for all \({\mathbb {P}}\in {\mathcal {P}}\).
As remarked inNutz (2015), the choice of \({\mathbb {F}}^{\mathbb {P}}_{+}\) in Definition 9 is the most general one. In fact an \({\mathbb {F}}\)-adapted and right-continuous process which is a local supermartingale with respect to \(({\mathbb {P}},\tilde {{\mathbb {F}}})\), for some \({\mathbb {F}}\subseteq \tilde {{\mathbb {F}}}\subseteq {\mathbb {F}}_{+}^{\mathbb {P}}\), is also a local supermartingale with respect to \(\left ({\mathbb {P}},{\mathbb {F}}_{+}^{\mathbb {P}}\right)\).
We now state a version of the optional decomposition theorem needed to show (38).
Theorem 3
(Theorem 2.4 from Nutz2015) Let \({\mathcal {P}}\) be a nonempty, saturated set of local martingale measures for S. If Y is a \({\mathcal {P}}\)-local supermartingale, then there exists an \({\mathbb {F}}\)-predictable process H which is S-integrable for every \({\mathbb {P}}\in {\mathcal {P}}\) and such that
It is important to remark that the choice of the filtration in Theorem 3 is completely arbitrary. However, it is also evident from (39) that Y and S must be measurable with respect to the same filtration.
Dynamic superhedging
We now focus on the study of the superreplication price at time t∈(0,T] of a \({\mathcal {G}}_{T}\)-measurable contingent claim.
Theorem 4
Suppose that \({\mathcal {P}}\) is a nonempty, saturated set of sigma martingale measures for S satisfying Assumption 1. Moreover, let f be an upper semianalytic, \({\mathcal {G}}_{T}\)-measurable function such that \({\mathcal {E}}_{0}(|f|) < \infty \). Consider the process Y=(Y t )t∈[0,T] given by the modification on a polar set of the process

Then, we have that for each t∈[0,T], \(Y_{t}=\pi ^{{\mathbb {P}}}_{t} {\mathbb {P}}\)-a.s. for each \({\mathbb {P}}\in {\mathcal {P}}\), where
forFootnote 4\({\mathbb {P}}\in {\mathcal {P}}\). In particular, if \(c_{t}\in {\mathcal {G}}_{t+}\) is such that there exists \(H\in {\mathcal {H}}\) with \(c_{t}+\int _{t}^{T} H_{s} dS_{s}\geq f {\mathbb {P}}-a.s.\) for all \({\mathbb {P}}\in {\mathcal {P}}\), then Y t ≤c t q.s.
Proof
The claim is obtained by proving the two quasi sure inequalities π t ≤Y t and π t ≥Y t . The first one can be shown as in the proof of Theorem 3.2 inNutz (2015). In fact, Theorem 3 applied with the σ-algebra \({\mathcal {G}}_{T}\) and the filtration \({\mathbb {G}}_{+}\) yields a process \(H\in {\mathcal {H}}\) such that
Being Y T =f q.s. (see Theorem 3.2 inNutz (2015)), we can argue from (41) that
from which follows Y t ≥π t q.s. On the other hand, let be given a \({\mathcal {G}}_{t+}\)-measurable random variable \(\bar {\pi }_{t}\) such that there exists a process \(H\in {\mathcal {H}}\) with the property that
For any rational number  it holds that
it holds that
From (42), exploiting the supermartingale property of \(\left (\int _{0}^{t} H_{s} dS_{s}\right)_{t\in [0,T]}\), we can deduce that
By the right continuity of \(\left (\int _{0}^{t} H_{s} dS_{s}\right)_{t\in [0,T]}\), we then have

and
We can conclude from (43) that \(\bar {\pi }_{t}\geq Y_{t}\) q.s., thanks to the definition of Y, which completes the proof. □
Remark 5
We do not include time 0 in our analysis as this case is already solved in Nutz (2015). Moreover, in his proof the author cleverly overcomes a subtle problem deriving from a direct application of Theorem 4 with t=0: the result would be an initial portfolio value which is \({\mathcal {G}}_{0+}\)-measurable, while it is desirable to have it deterministic as obtained in Theorem 3.2 in Nutz (2015).
Unfortunately it is not possible to extend this result for t>0, i.e. to obtain that Y t is \(\mathcal {G}_{t}\)-measurable for t>0, in the more general framework we considered in this section. This problem already arises for the dynamic super hedging duality shown in Proposition 4.5 inNutz and Soner (2012) in a less general context than ours. We now outline why, following the proof of Theorem 3.2 inNutz (2015). More precisely, we show that it is not always possible to prove that the conditional sublinear expectation is a version of the dynamic superreplication price. Given an upper semianalytic function f with \({\mathcal {E}}_{0}(|f|)<\infty \), the issue lies in the possibility to find a process \(H\in {\mathcal {H}}\) such that
which is equivalent to show that \(Y_{t}\leq {\mathcal {E}}_{t}(f) {\mathbb {P}}\)-a.s. for every \({\mathbb {P}}\in {\mathcal {P}}\), where Y is a modification of the process defined in (40). To this end, fix \({\mathbb {P}}\in {\mathcal {P}}\). It follows from Theorem VI.2 inDellacherie et al. (1982) that
Therefore, with the same argument as in Proposition 1, we obtain
Let then \(\pi _{t}^{\mathbb {P}}\) be the smallest \({\mathcal {F}}_{T}\)-measurable random variable dominating \(Y_{t} {\mathbb {P}}\)-a.s. To reach the same conclusion as inNutz (2015), we would need to prove that
However, thanks to Theorem 2.1.6 inTutsch (2006),
where the supremum is taken over all the probability measures \({\mathbb {Q}}\) on \({\mathcal {F}}_{T}\) that are equivalent to \({\mathbb {P}}\), which contradicts (44) already in the simple case of a complete market with unique prior.
Of course, a sufficient condition to immediately achieve the equality \(Y={\mathcal {E}}(f)\) q.s. would be the right continuity of the process \({\mathcal {E}}(f)\), because of (40). However, such a property does not hold in general. As a concrete model in which the sublinear operator is not right-continuous, we refer to Example 4.6 inNutz and Soner (2012).
The superreplication problem is namely solved in a more satisfactory way in the G-framework. It is an important result ofNutz and Van Handel (2013) that the G-expectation framework can be incorporated in the model described above. More precisely, consider the set of martingale measures
where B=(B u )u≥0 with B u (ω)=ω u denotes the canonical process, and its subset
where now \(\langle B\rangle ^{\mathbb {P}}\) is the  -valued quadratic variation process of B under \({\mathbb {P}}\) and absolute continuity refers to the Lebesgue measure. We report here Proposition 3.1 fromNutz and Van Handel (2013).
-valued quadratic variation process of B under \({\mathbb {P}}\) and absolute continuity refers to the Lebesgue measure. We report here Proposition 3.1 fromNutz and Van Handel (2013).
Proposition 7
The set
where D is a nonempty, convex, and compact subset of  , satisfies Assumption 1.
, satisfies Assumption 1.
It is indeed well known (see Nutz and Van Handel2013) that the sublinear expectation
yields the G-expectation on the space of quasi continuous functions in \(\mathbb {L}^{1}_{G}\), where for all β≥1
and \(\mathcal {B}(\Omega _{T})\) is the Borel σ-algebra of Ω T , seePeng (2007).
Given a \({\mathcal {F}}_{T}\)-measurable claim \(f\in \mathbb {L}^{\beta }_{G}\), β>1, it is easy to show that \(\pi _{t}={\mathcal {E}}_{t}^{\mathbf {D}}(f)\), for every t∈[0,T]. The crucial difference is that the literature on G-expectation provides a G-martingale representation theorem and not only an optional decomposition result.
Remark 6
For simplicity, thanks to the results of Proposition 7 we will denote with \(E_{G}[f]:={\mathcal {E}}_{0}^{\mathbf {D}}(f)\) the G-expectation of a random variable in \(\mathbb {L}^{1}_{G}\) and with \(E_{G}\left [f|{\mathcal {F}}_{t}\right ]:={\mathcal {E}}_{t}^{\mathbf {D}}(f)\) the relative conditional G-expectation at time t.
Theorem 5
(Theorem 4.5 of Song2011) Let β>1 and \(H\in \mathbb {L}_{G}^{\beta }({\mathcal {F}}_{T})\). Then the G-martingale M with \(M_{t}:=E_{G}(H|\mathcal {F}_{t})\), t∈[0,T], has the following representation
where K is a continuous, increasing process with K0=0, \(K_{T}\in L_{G}^{\alpha }({\mathcal {F}}_{T})\), \(\theta \in M_{G}^{\alpha }(0,T)\)Footnote 5, ∀α∈[1,β), and −K is a G-martingale.
In the G-setting, obtaining the dynamic superreplication price of f follows from the decomposition of the G-martingale \((E_{G}[f|{\mathcal {F}}_{t}])_{t\in [0,T]}\). Showing that \(\pi _{t}\geq E_{G}[f|{\mathcal {F}}_{t}]\) q.s. is analogous to what is done in Theorem 4, while using Theorem 5 we get
for every t∈[0,T] and suitable processes θ and K. It is then apparent that
giving the increasing property of K, from which we can argue \(\pi _{t}\leq E_{G}[f|{\mathcal {F}}_{t}]\).
We conclude by providing the following result fromBiagini and Zhang (2017), which shows sufficient conditions for having right-continuity of the sublinear operator.
Proposition 8
(Proposition 2.6 of Biagini and Zhang2017) If \({\mathcal {P}}\) is a tight family satisfying Assumption 1 and X is an upper semianalytic function which is bounded and continuous on a set \(A \in \mathcal {B}(\Omega)\) such that P(Ac)=0 for every \(P \in {\mathcal {P}}\), then the process \(({\mathcal {E}}_{t}(X))_{t \geq 0}\) is càdlàg.
Notes
An
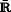 -valued function f is called upper semianalytic if {f>c} is analytic for each
-valued function f is called upper semianalytic if {f>c} is analytic for each 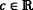 .
.\(\int _{0}^{t} H_{s} dS_{s}\) denotes the usual stochastic (Itô) integral under the probability \({\mathbb {P}}\). Note that this definition avoids aggregation issues since the property must hold for each \({\mathbb {P}}\).
\({\mathcal {P}}\) defined in (17) is m-stable if for elements \({\mathbb {Q}}^{0}\in {\mathcal {P}}\), \({\mathbb {Q}}\in {\mathcal {P}}\) such that \({\mathbb {Q}}\sim {\mathbb {P}}\), with associate martingales \(Z_{t}^{0}=E\left [\frac {d{\mathbb {Q}}^{0}}{d{\mathbb {P}}}|{\mathcal {F}}_{t}\right ]\) and \(Z_{t}=E\left [\frac {d{\mathbb {Q}}}{d{\mathbb {P}}}|{\mathcal {F}}_{t}\right ]\), and for each stopping time τ, the element L defined as \(L_{t}=Z_{t}^{0}\) for t≤τ and \(L_{t}=Z_{T}^{0}Z_{t}/Z_{T}\) for t≥τ is a martingale that defines an element in \({\mathcal {P}}\). We also assume that every \({\mathcal {F}}_{0}\)-measurable non-negative function Z0 such that \(E_{\mathbb {P}}[Z_{0}]=1\), defines an element \(d{\mathbb {Q}}=Z_{0}d{\mathbb {P}}\) that is in \({\mathcal {P}}\).
Here \({\text {ess\,inf}}^{{\mathbb {P}}}\) denotes the essential supremum with respect to the probability measure \({\mathbb {P}}\). We use this notation only when it is not clear under which prior the essential supremum is taken.
The space \(M_{G}^{\alpha }(0,T)\) is defined as the completion under the norm \(\Vert \eta \Vert _{M_{G}^{\alpha }(0,T)}=E_{G}\left [\left (\int _{0}^{T}|\eta _{s}|^{2}ds\right)^{p/2}\right ]^{1/p}\) of the collection of processes η of the form \(\eta _{t}=\sum _{j=0}^{n-1}\xi _{j}{\mathbf {1}}_{\{{[t_{j},t_{j+1})}\}}(t)\), where {t0,…,t n } is a partition of [0,T] and ξ j is a \({\mathcal {F}}_{t_{j}}\)-measurable, cylindrical random variable.
References
Ash, R: Real analysis and probability. Academic Press, New York (1972).
Beissner, P: Coherent Price Systems and Uncertainty-Neutral Valuation. Working Paper 464, Center for Mathematical Economics, Bielefeld University (2012).
Biagini, F, Föllmer, H, Nedelcu, S: Shifting martingale measures and the slow birth of a bubble as a submartingale. Finance Stochast. 18(2), 297–326 (2014).
Biagini, F, Nedelcu, S: The formation of financial bubbles in defaultable markets. SIAM J. Financ. Math. 6(1), 530–558 (2015).
Biagini, F, Zhang, Y: Reduced-form framework and superhedging for payment streams under model uncertainty. arXiv:1707.04475 (2017).
Biagini, S, Bouchard, B, Kardaras, C, Nutz, M: Robust fundamental theorem for continuous processes. Mathematical Finance.27, 963–987 (2017). doi:10.1111/mafi.12110.
Bouchard, B, Nutz, M: Arbitrage and duality in nondominated discrete-time models. Ann. Appl. Probab. 25(2), 823–859 (2015).
Burzoni, M, Riedel, F, Soner, HM: Viability and arbitrage under knightian uncertainty (2017). arXiv:1707.03335.
Cohen, S: Quasi-sure analysis, aggregation and dual representations of sublinear expectations in general spaces. Electron. J. Probab. 17(62), 1–15 (2012).
Cox, AMG, Hobson, DG: Local martingales, bubbles and option prices. Finance Stochast. 9(4), 477–492 (2005).
Cox, AMG, Hou, Z, Obłój, J: Robust pricing and hedging under trading restrictions and the emergence of local martingale models.Finance Stoch. 20, 669 (2016). https://doi.org/10.1007/s00780-016-0293-3.
Delbaen, F: The structure of m–stable sets and in particular of the set of risk neutral measures, volume 1874 of Lecture Notes in Math. Springer, Berlin Heidelberg (2006).
Dellacherie, C, Meyer, P: Probabilities and potential B. North-Holland Publishing Co., Amsterdam (1982).
Elworthy, KD, Li, X-M, Yor, M: The importance of strictly local martingales; applications to radial Ornstein–Uhlenbeck processes. Probab. Theory Relat. Fields. 115(3), 325–355 (1999).
Föllmer, H, Protter, P: Local martingales and filtration shrinkage. ESAIM Probab. Stat. 15, S25–S38 (2011).
Föllmer, H, Schied, A: Stochastic Finance. An Introduction in Discrete Time. 3rd edition. De Gruyter, Berlin (2011).
Herdegen, M, Schweizer, M: Strong bubbles and strict local martingales. Int. J. Theor. Appl. Finance. 19, 1650022 (2016).
Hugonnier, J: Rational asset pricing bubbles and portfolio constraints. J. Economic Theory. 147(6), 2260–2302 (2012).
Jarrow, RA, Larsson, M: The meaning of market efficiency. Math. Financ. 22(1), 1–30 (2012).
Jarrow, RA, Protter, P, Roch, A: A liquidity based model for asset price bubble. Quant. Finan. 12(9), 1339–1349 (2012).
Jarrow, RA, Protter, P, Shimbo, K: Asset price bubbles in complete markets, pp. 97–121. Advances in Mathematical Finance, Birkhäuser Boston (2007).
Jarrow, RA, Protter, P, Shimbo, K: Asset price bubbles in incomplete markets. Math. Financ. 20(2), 145–185 (2010).
Kramkov, DO: Optional decomposition of supermartingales and hedging contingent claims in incomplete security markets. Probab. Theory Relat. Fields. 105(4), 459–479 (1996).
Loewenstein, M, Willard, GA: Rational equilibrium and asset-pricing bubbles in continuous trading models. J. Econ. Theory. 91(1), 17–58 (2000).
Luo, P, Wang, F: Stochastic differential equations driven by G-brownian motion and ordinary differential equations. Stoch. Process. Appl. 124(11), 3869–3885 (2014).
Merton, RC: Theory of rational option pricing. Bell J. Econ. Manag. Sci. 4(1), 141–183 (1973).
Nutz, M: Robust superhedging with jumps and diffusion. Stoch. Process. Appl. 125(12), 4543–4555 (2015).
Nutz, M, Soner, HM: Superhedging and dynamic risk measures under volatility uncertainty. SIAM J Control. Optim. 50(4), 2065–2089 (2012).
Nutz, M, Van Handel, R: Constructing sublinear expectations on path space.Stoch. Process. Appl. 123(8), 3100–3121 (2013).
Pal, S, Protter, P: Analysis of continuous strict local martingales via h-transforms. Stoch. Process. Appl. 120(8), 1424–1443 (2010).
Peng, S: G-expectation, G-Brownian motion and related stochastic calculus of Ito typê. Stoch. Anal. Appl. 2, 541–567 (2007).
Peng, S: Nonlinear expectations and stochastic calculus under uncertainty. (2010). http://arxiv.org/abs/1002.4546.
Protter, P: A mathematical theory of financial bubbles. In: Paris-Princeton Lectures on Mathematical Finance 2013. Lecture Notes in Mathematics, vol 2081, pp. 1–108. Springer, Cham (2013).
Revuz, D, Yor, M: Continuous Martingales and Brownian Motion. third edition. Springer, Berlin Heidelberg (1999).
Soner, HM, Touzi, N, Zhang, J: Martingale representation theorem for the G-expectation. Stoch. Process. Appl. 121(2), 265–287 (2011a).
Soner, HM, Touzi, N, Zhang, J: Quasi-sure stochastic analysis through aggregation. Electron. J. Probab. 16, 1844–1879 (2011b).
Soner, HM, Touzi, N, Zhang, J: Dual formulation of second order target problems. Ann. Appl. Probab. 23(1), 308–347 (2013).
Song, Y: Some properties of G-evaluation and its applications to G-martingale decomposition. Sci. China Math. 54(2), 287–300 (2011).
Stricker, C: Quasimartingales, martingales locales, semimartingales et filtration naturelle. Z. Wahrscheinlichkeitstheorie verw. Gebiete. 39(1), 55–63 (1977).
Tutsch, D: Konsistente und konsequente dynamische Risikomaße und das Problem der Aktualisierung (2006). PhD thesis, Humboldt-Universität zu Berlin.
Acknowledgements
The authors would like to thank two anonymous referees for a very careful reading and a number of helpful comments that helped to sensibly improve the quality of the paper.
Author information
Authors and Affiliations
Contributions
Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Biagini, F., Mancin, J. Financial asset price bubbles under model uncertainty. Probab Uncertain Quant Risk 2, 14 (2017). https://doi.org/10.1186/s41546-017-0026-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41546-017-0026-3
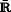 -valued function f is called upper semianalytic if {f>c} is analytic for each
-valued function f is called upper semianalytic if {f>c} is analytic for each 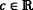 .
.