- Research
- Open access
- Published:
Convergence to a self-normalized G-Brownian motion
Probability, Uncertainty and Quantitative Risk volume 2, Article number: 4 (2017)
Abstract
G-Brownian motion has a very rich and interesting new structure that nontrivially generalizes the classical Brownian motion. Its quadratic variation process is also a continuous process with independent and stationary increments. We prove a self-normalized functional central limit theorem for independent and identically distributed random variables under the sub-linear expectation with the limit process being a G-Brownian motion self-normalized by its quadratic variation. To prove the self-normalized central limit theorem, we also establish a new Donsker’s invariance principle with the limit process being a generalized G-Brownian motion.
Introduction
Let {X
n
;n≥1} be a sequence of independent and identically distributed random variables on a probability space  . Set \(S_{n}=\sum _{j=1}^{n} X_{j}\). Suppose EX
1=0 and \(EX_{1}^{2}=\sigma ^{2}>0\). The well-known central limit theorem says that
. Set \(S_{n}=\sum _{j=1}^{n} X_{j}\). Suppose EX
1=0 and \(EX_{1}^{2}=\sigma ^{2}>0\). The well-known central limit theorem says that
or, equivalently, for any bounded continuous function ψ(x),
where ξ∼N(0,σ 2) is a normal random variable. If the normalization factor \(\sqrt {n}\) is replaced by \(\sqrt {V_{n}}\), where \(V_{n}=\sum _{j=1}^{n} X_{j}^{2}\), then
Giné et al. (1997) proved that (3) holds if and only if EX 1=0 and
The result (3) is refered to as the self-normalized central limit theorem. The purpose of this paper is to establish the self-normalized central limit theorem under the sub-linear expectation.
The sub-linear expectation, or also called G-expectation, is a nonlinear expectation generalizing the notions of backward stochastic differential equations, g-expectations, and provides a flexible framework to model non-additive probability problems and the volatility uncertainty in finance. Peng (2006, 2008a,b) introduced a general framework of the sub-linear expectation of random variables and the notions of the G-normal random variable, G-Brownian motion, independent and identically distributed random variables, etc., under the sub-linear expectation. The construction of sub-linear expectations on the space of continuous paths and discrete-time paths can also be founded in Yan et al. (2012) and Nutz and van Handel (2013). For basic properties of the sub-linear expectation, one can refer to Peng (2008b, 2009, 2010a etc.). For stochastic calculus and stochastic differential equations with respect to a G-Brownian motion, one can refer to Li and Peng (2011), Hu et al. (2014a, b), etc., and a book by Peng (2010a).
The central limit theorem under the sub-linear expectation was first established by Peng (2008b). It says that (2) remains true when the expectation E is replaced by a sub-linear expectation \(\hat {\mathbb {E}}\) if {X n ;n≥1} are independent and identically distributed under \(\hat {\mathbb {E}}\), i.e.,
where ξ is a G-normal random variable.
In the classical case, when \(\textsf {E}[X_{1}^{2}]\) is finite, (3) follows from the cental limit theorem (1) directly by Slutsky’s lemma and the fact that
The latter is due to the law of large numbers. Under the framework of the sub-linear expectation, \(\frac {V_{n}}{n}\) no longer converges to a constant. The self-normalized central limit theorem cannot follow from the central limit theorem (5) directly. In this paper, we will prove that
where W t is a G-Brownian motion and 〈W〉 t is its quadratic variation process. A very interesting phenomenon of G-Brownian motion is that its quadratic variation process is also a continuous process with independent and stationary increments, and thus can still be regarded as a Brownian motion. When the sub-linear expectation \(\hat {\mathbb {E}}\) reduces to a linear one, W t is the classical Brownian motion with W 1∼N(0,σ 2) and 〈W〉 t =t σ 2, and then (6) is just (3). Our main results on the self-normalized central limit theorem will be given in Section “Main results”, where the process of the self-normalized partial sums \({S_{[nt]}}/{\sqrt {V_{n}}}\) is proved to converge to a self-normalized G-Brownian motion \({W_{t}}/{\sqrt {\langle W\rangle _{1}}}\). We also consider the case in which the second moments of X i ’s are infinite and obtain the self-normalized central limit theorem under a condition similar to (4). In the next section, we state basic settings in a sub-linear expectation space, including capacity, independence, identical distribution, G-Brownian motion, etc. One can skip this section if these concepts are familiar. To prove the self-normalized central limit theorem, we establish a new Donsker’s invariance principle in Section “Invariance principle” with the limit process being a generalized G-Brownian motion. The proof is given in the last section.
Basic settings
We use the framework and notations of Peng (2008b). Let \((\Omega,\mathcal F)\) be a given measurable space and let  be a linear space of real functions defined on \((\Omega,\mathcal F)\) such that if
be a linear space of real functions defined on \((\Omega,\mathcal F)\) such that if  , then
, then  for each \(\varphi \in C_{b}(\mathbb {R}^{n})\bigcup C_{l,Lip}(\mathbb {R}^{n})\), where \(C_{b}(\mathbb R^{n})\) denotes the space of all bounded continuous functions and \(C_{l,Lip}(\mathbb {R}^{n})\) denotes the linear space of (local Lipschitz) functions φ satisfying
for each \(\varphi \in C_{b}(\mathbb {R}^{n})\bigcup C_{l,Lip}(\mathbb {R}^{n})\), where \(C_{b}(\mathbb R^{n})\) denotes the space of all bounded continuous functions and \(C_{l,Lip}(\mathbb {R}^{n})\) denotes the linear space of (local Lipschitz) functions φ satisfying
 is considered as a space of “random variables.” In this case, we denote
is considered as a space of “random variables.” In this case, we denote  . Further, we let \(C_{b,Lip}(\mathbb R^{n})\) denote the space of all bounded and Lipschitz functions on \(\mathbb R^{n}\).
. Further, we let \(C_{b,Lip}(\mathbb R^{n})\) denote the space of all bounded and Lipschitz functions on \(\mathbb R^{n}\).
Sub-linear expectation and capacity
Definition 1
A sub-linear expectation
\(\hat {\mathbb {E}}\) on  is a function
is a function  satisfying the following properties: for all
satisfying the following properties: for all  , we have
, we have
-
(a)
Monotonicity: If X≥Y then \(\hat {\mathbb {E}} [X]\ge \hat {\mathbb {E}} [Y]\);
-
(b)
Constant preserving:\(\hat {\mathbb {E}} [c] = c\);
-
(c)
Sub-additivity:\(\hat {\mathbb {E}}[X+Y]\le \hat {\mathbb {E}} [X] +\hat {\mathbb {E}} [Y ]\) whenever \(\hat {\mathbb {E}} [X] +\hat {\mathbb {E}} [Y ]\) is not of the form +∞−∞ or −∞+∞;
-
(d)
Positive homogeneity:\(\hat {\mathbb {E}} [\lambda X] = \lambda \hat {\mathbb {E}} [X]\), λ≥0.
Here \(\overline {\mathbb R}=[-\infty, \infty ]\). The triple  is called a sub-linear expectation space. Given a sub-linear expectation \(\hat {\mathbb {E}} \), let us denote the conjugate expectation \(\widehat {\mathcal {E}}\)of \(\hat {\mathbb {E}}\) by
is called a sub-linear expectation space. Given a sub-linear expectation \(\hat {\mathbb {E}} \), let us denote the conjugate expectation \(\widehat {\mathcal {E}}\)of \(\hat {\mathbb {E}}\) by

Next, we introduce the capacities corresponding to the sub-linear expectations. Let \(\mathcal G\subset \mathcal F\). A function \(V:\mathcal G\rightarrow [0,1]\) is called a capacity if
It is called sub-additive if \(V(A\bigcup B)\le V(A)+V(B)\) for all \(A,B\in \mathcal G\) with \(A\bigcup B\in \mathcal G\).
Let  be a sub-linear space and \(\widehat {\mathcal {E}} \) be the conjugate expectation of \(\hat {\mathbb {E}}\). We introduce the pair \((\mathbb {V},\mathcal {V})\) of capacities by setting
be a sub-linear space and \(\widehat {\mathcal {E}} \) be the conjugate expectation of \(\hat {\mathbb {E}}\). We introduce the pair \((\mathbb {V},\mathcal {V})\) of capacities by setting

where A c is the complement set of A. Then, \(\mathbb {V}\) is sub-additive and

Further, we define an extension of \(\hat {\mathbb {E}}^{\ast }\) of \(\hat {\mathbb {E}}\) by

where inf∅=+∞. Then,

Independence and distribution
Definition 2
-
(i)
(Identical distribution) Let X 1 and X 2 be two n-dimensional random vectors defined, respectively, in sub-linear expectation spaces
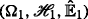 and
and 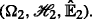 . They are called identically distributed, denoted by \(\boldsymbol X_{1}\overset {d}= \boldsymbol X_{2}\) if
$$ \hat{\mathbb{E}}_{1}[\varphi(\boldsymbol X_{1})]=\hat{\mathbb{E}}_{2}[\varphi(\boldsymbol X_{2})], \;\; \forall \varphi\in C_{l,Lip}(\mathbb R^{n}), $$
. They are called identically distributed, denoted by \(\boldsymbol X_{1}\overset {d}= \boldsymbol X_{2}\) if
$$ \hat{\mathbb{E}}_{1}[\varphi(\boldsymbol X_{1})]=\hat{\mathbb{E}}_{2}[\varphi(\boldsymbol X_{2})], \;\; \forall \varphi\in C_{l,Lip}(\mathbb R^{n}), $$whenever the sub-expectations are finite. A sequence {X n ;n≥1} of random variables is said to be identically distributed if \(X_{i}\overset {d}= X_{1}\) for each i≥1.
-
(ii)
(Independence) In a sub-linear expectation space
 , a random vector
, a random vector 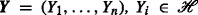 is said to be independent to another random vector
is said to be independent to another random vector 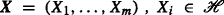 under \(\hat {\mathbb {E}}\) if for each test function \(\varphi \in C_{l,Lip}(\mathbb R^{m} \times \mathbb R^{n})\) we have
$$ \hat{\mathbb{E}} [\varphi(\boldsymbol{X}, \boldsymbol{Y})] = \hat{\mathbb{E}} \left[\hat{\mathbb{E}}[\varphi(\boldsymbol{x}, \boldsymbol{Y})]\big|_{\boldsymbol{x}=\boldsymbol{X}}\right], $$
under \(\hat {\mathbb {E}}\) if for each test function \(\varphi \in C_{l,Lip}(\mathbb R^{m} \times \mathbb R^{n})\) we have
$$ \hat{\mathbb{E}} [\varphi(\boldsymbol{X}, \boldsymbol{Y})] = \hat{\mathbb{E}} \left[\hat{\mathbb{E}}[\varphi(\boldsymbol{x}, \boldsymbol{Y})]\big|_{\boldsymbol{x}=\boldsymbol{X}}\right], $$whenever \(\overline {\varphi }(\boldsymbol {x}):=\hat {\mathbb {E}}\left [|\varphi (\boldsymbol {x}, \boldsymbol {Y})|\right ]<\infty \) for all x and \(\hat {\mathbb {E}}\left [|\overline {\varphi }(\boldsymbol {X})|\right ]<\infty \).
-
(iii)
(IID random variables) A sequence of random variables {X n ;n≥1} is said to be independent and identically distributed (IID), if \(X_{i}\overset {d}=X_{1}\) and X i+1 is independent to (X 1,…,X i ) for each i≥1.
G-normal distribution, G-Brownian motion and its quadratic variation
Let \(0<\underline {\sigma }\le \overline {\sigma }<\infty \) and \(G(\alpha)=\frac {1}{2}\left (\overline {\sigma }^{2} \alpha ^{+} - \underline {\sigma }^{2} \alpha ^{-}\right)\). X is called a normal \(N\left (0, \left [\underline {\sigma }^{2}, \overline {\sigma }^{2}\right ]\right)\) distributed random variable (written as \(X\sim N\left (0, \left [\underline {\sigma }^{2}, \overline {\sigma }^{2}\right ]\right)\)) under \(\hat {\mathbb {E}}\), if for any bounded Lipschitz function φ, the function \(u(x,t)=\hat {\mathbb {E}}\left [\varphi \left (x+\sqrt {t} X\right)\right ]\) (\(x\in \mathbb R, t\ge 0\)) is the unique viscosity solution of the following heat equation:
Let C[0,1] be a function space of continuous functions on [0,1] equipped with the supremum norm \(\|x\|=\sup \limits _{0\le t\le 1}|x(t)|\) and C b (C[0,1]) is the set of bounded continuous functions \(h(x):C[0,1]\rightarrow \mathbb R\). The modulus of the continuity of an element x∈C[0,1] is defined by
It is showed that there is a sub-linear expectation space  with \(\widetilde {\Omega }= C[0,1]\) and
with \(\widetilde {\Omega }= C[0,1]\) and  such that
such that  is a Banach space, and the canonical process \(W(t)(\omega) = \omega _{t} (\omega \in \widetilde {\Omega })\) is a G-Brownian motion with \(W(1)\sim N\left (0, \left [\underline {\sigma }^{2}, \overline {\sigma }^{2}\right ]\right)\) under \(\widetilde {\mathbb E}\), i.e., for all 0≤t
1<…<t
n
≤1, \(\varphi \in C_{l,lip}(\mathbb R^{n})\),
is a Banach space, and the canonical process \(W(t)(\omega) = \omega _{t} (\omega \in \widetilde {\Omega })\) is a G-Brownian motion with \(W(1)\sim N\left (0, \left [\underline {\sigma }^{2}, \overline {\sigma }^{2}\right ]\right)\) under \(\widetilde {\mathbb E}\), i.e., for all 0≤t
1<…<t
n
≤1, \(\varphi \in C_{l,lip}(\mathbb R^{n})\),
where \(\psi \left (x_{1},\ldots, x_{n-1}\right)\big)=\widetilde {\mathbb {E}}\left [\varphi \left (x_{1},\ldots, x_{n-1}, \sqrt {t_{n}-t_{n-1}}W(1)\right)\right ]\) (cf. Peng (2006, 2008a, 2010a), Denis et al. (2011)).
The quadratic variation process of a G-Brownian motion W is defined by
where \(\Pi _{t}^{N}=\left \{t_{0}^{N},t_{1}^{N},\ldots, t_{N}^{n}\right \}\) is a partition of [0,t] and \(\left \|\Pi _{t}^{N}\right \|=\max _{j}\left |t_{j}^{N}-t_{j-1}^{N}\right |\), and the limit is taken in L 2, i.e.,
The quadratic variation process 〈W〉 t is also a continuous process with independent and stationary increments. For the properties and the distribution of the quadratic variation process, one can refer to a book by Peng (2010a).
Denis et al. (2011) showed the following representation of the G-Brownian motion (cf. Theorem 52).
Lemma 1
Let  be a probability measure space and {B(t)}
t≥0 is a P-Brownian motion. Then, for all bounded continuous functions \(\varphi : C_{b}[0,1]\rightarrow \ \mathbb R\),
be a probability measure space and {B(t)}
t≥0 is a P-Brownian motion. Then, for all bounded continuous functions \(\varphi : C_{b}[0,1]\rightarrow \ \mathbb R\),
where

For the reminder of this paper, the sequences {X
n
;n≥1}, {Y
n
;n≥1}, etc., of the random variables are considered in  . Without specification, we suppose that {X
n
;n≥1} is a sequence of independent and identically distributed random variables in
. Without specification, we suppose that {X
n
;n≥1} is a sequence of independent and identically distributed random variables in  with \(\hat {\mathbb {E}}[X_{1}]=\widehat {\mathcal {E}}[X_{1}]=0\), \(\hat {\mathbb {E}}\left [X_{1}^{2}\right ]=\overline {\sigma }^{2}\), and \(\widehat {\mathcal {E}}\left [X_{1}^{2}\right ]=\underline {\sigma }^{2}\). Denote \(S_{0}^{X}=0\), \(S_{n}^{X}=\sum _{k=1}^{n} X_{k}\), V
0=0, \(V_{n}=\sum _{k=1}^{n} X_{k}^{2}\). And suppose that
with \(\hat {\mathbb {E}}[X_{1}]=\widehat {\mathcal {E}}[X_{1}]=0\), \(\hat {\mathbb {E}}\left [X_{1}^{2}\right ]=\overline {\sigma }^{2}\), and \(\widehat {\mathcal {E}}\left [X_{1}^{2}\right ]=\underline {\sigma }^{2}\). Denote \(S_{0}^{X}=0\), \(S_{n}^{X}=\sum _{k=1}^{n} X_{k}\), V
0=0, \(V_{n}=\sum _{k=1}^{n} X_{k}^{2}\). And suppose that  is a sub-linear expectation space which is rich enough such that there is a G-Brownian motion W(t) with \(W(1)\sim N\left (0,\left [\underline {\sigma }^{2},\overline {\sigma }^{2}\right ]\right)\). We denote a pair of capacities corresponding to the sub-linear expectation \(\widetilde {\mathbb E}\) by \(\left (\widetilde {\mathbb {V}},\widetilde {\mathcal {V}}\right)\), and the extension of \(\widetilde {\mathbb E}\) by \(\widetilde {\mathbb {E}}^{\ast }\).
is a sub-linear expectation space which is rich enough such that there is a G-Brownian motion W(t) with \(W(1)\sim N\left (0,\left [\underline {\sigma }^{2},\overline {\sigma }^{2}\right ]\right)\). We denote a pair of capacities corresponding to the sub-linear expectation \(\widetilde {\mathbb E}\) by \(\left (\widetilde {\mathbb {V}},\widetilde {\mathcal {V}}\right)\), and the extension of \(\widetilde {\mathbb E}\) by \(\widetilde {\mathbb {E}}^{\ast }\).
Main results
We consider the convergence of the process \(S_{[nt]}^{X}\). Because it is not in C[0,1], it needs to be modified. Define the C[0,1]-valued random variable \(\widetilde {S}_{n}^{X}(\cdot)\) by setting
Then, \( \widetilde {S}_{n}^{X}(t)=S_{[nt]}^{X}+(nt-[nt])X_{[nt]+1}\). Here [nt] is the largest integer less than or equal to nt. Zhang (2015) obtained the functional central limit theorem as follows.
Theorem 1
Suppose \(\hat {\mathbb {E}}\left [\left (X_{1}^{2}-b\right)^{+}\right ]\rightarrow 0\) as b→∞. Then, for all bounded continuous functions \(\varphi :C[0,1]\rightarrow \mathbb {R}\),
Replacing the normalization factor \(\sqrt {n}\) by \(\sqrt {V_{n}}\), we obtain the self-normalized process of partial sums:
where \(\frac {0}{0}\) is defined to be 0. Our main result is the following self-normalized functional central limit theorem (FCLT).
Theorem 2
Suppose \(\hat {\mathbb {E}}\left [\left (X_{1}^{2}-b\right)^{+}\right ]\rightarrow 0\) as b→∞. Then, for all bounded continuous functions \(\varphi :C[0,1]\rightarrow \mathbb {R}\),
In particular, for all bounded continuous functions \(\varphi :\mathbb {R}\rightarrow \mathbb {R}\),
Remark 1
It is obvious that
An interesting problem is how to estimate the upper bounds of the expectations on the right hand side of (10) and (11).
Further, \(\frac {W(\cdot)}{\sqrt {\langle W\rangle _{1}}}\overset {d}=\frac {\overline {W}(\cdot)}{\sqrt {\langle \overline {W}\rangle _{1}}}\), where \(\overline {W}(t)\) is a G-Brownian motion with \(\overline {W}(1)\sim N(0,[r^{-2},1])\), \(r^{2}=\overline {\sigma }^{2}/\underline {\sigma }^{2}\).
For the classical self-normalized central limit theorem, Giné et al. (1997) showed that the finiteness of the second moments can be relaxed to the condition (4). Csörgő et al. (2003) proved the self-normalized functional central limit theorem under (4). The next theorem gives a similar result under the sub-linear expectation and is an extension of Theorem 2.
Theorem 3
Let {X
n
;n≥1} be a sequence of independent and identically distributed random variables in the sub-linear expectation space  with \(\hat {\mathbb {E}}[X_{1}]=\widehat {\mathcal {E}}[X_{1}]=0\). Denote \(l(x)=\hat {\mathbb {E}}\left [X_{1}^{2}\wedge x^{2}\right ]\). Suppose
with \(\hat {\mathbb {E}}[X_{1}]=\widehat {\mathcal {E}}[X_{1}]=0\). Denote \(l(x)=\hat {\mathbb {E}}\left [X_{1}^{2}\wedge x^{2}\right ]\). Suppose
-
(I)
\(x^{2}\mathbb {V}(|X_{1}|\ge x)=o\left (l(x)\right)\) as x→∞;
-
(II)
\({\lim }_{x\rightarrow \infty } \frac {\hat {\mathbb {E}}\left [X_{1}^{2}\wedge x^{2}\right ]}{\widehat {\mathcal {E}}\left [X_{1}^{2}\wedge x^{2}\right ]}=r^{2}<\infty \);
-
(III)
\(\hat {\mathbb {E}}[(|X_{1}|-c)^{+}]\rightarrow 0\) as c→∞.
Then, the conclusions of Theorem 2 remain true with W(t) being a G-Brownian motion such that W(1)∼N(0,[r −2,1]).
Remark 2
Note for c>1, \(l(cx)=\hat {\mathbb {E}}\left [X_{1}^{2}\wedge (cx)^{2}\right ]\le l(x)+(cx)^{2}\mathbb {V}(|X_{1}|\ge x)\). Condition (I) implies that l(cx)/l(x)→1 as x→∞, i.e., l(x) is a slowly varying function. Therefore, there is a constant C such that \(\int _{x}^{\infty }y^{-2}l(y)dy \le C x^{-1} l(x)\) if x is large enough. So, \(\int _{x}^{\infty }\mathbb {V}(|X_{1}|\ge y)dy=o(x^{-1}l(x))\). Also, by Lemma 3.9 (b) of Zhang (2016), condition (III) implies that \(\hat {\mathbb {E}}\left [(|X_{1}|-x)^{+}\right ]\le \int _{x}^{\infty }\mathbb {V}(|X_{1}|\ge y)dy\). Hence, \(\hat {\mathbb {E}}\left [\left (|X_{1}|-x\right)^{+}\right ]=o(x^{-1}l(x))\) if conditions (I) and (III) are satisfied. When \(\hat {\mathbb {E}}\) is a continuous sub-linear expectation, then for any random variable Y we have \(\hat {\mathbb {E}}[|Y|]\le \int _{0}^{\infty }\mathbb {V}(|Y|\ge y)dy\) by Lemma 3.9 (c) of Zhang (2016), and so the condition (III) can be removed. Here, \(\hat {\mathbb {E}}\) is called continuous if, for any  with \(\hat {\mathbb {E}}[X_{n}],\hat {\mathbb {E}}[X]<\infty \), \(\hat {\mathbb {E}}[X_{n}]\nearrow \hat {\mathbb {E}}[X]\) whenever 0≤X
n
↗X, and, \(\hat {\mathbb {E}}[X_{n}]\searrow \hat {\mathbb {E}}[X]\) whenever X
n
↘X.
with \(\hat {\mathbb {E}}[X_{n}],\hat {\mathbb {E}}[X]<\infty \), \(\hat {\mathbb {E}}[X_{n}]\nearrow \hat {\mathbb {E}}[X]\) whenever 0≤X
n
↗X, and, \(\hat {\mathbb {E}}[X_{n}]\searrow \hat {\mathbb {E}}[X]\) whenever X
n
↘X.
Invariance principle
To prove Theorems 2 and 3, we will prove a new Donsker’s invariance principle. Let {(X
i
,Y
i
);i≥1} be a sequence of independent and identically distributed random vectors in the sub-linear expectation space  with \(\hat {\mathbb {E}}[X_{1}]=\hat {\mathbb {E}}[-X_{1}]=0\), \(\hat {\mathbb {E}}[X_{1}^{2}]=\overline {\sigma }^{2}\), \(\widehat {\mathcal {E}}[X_{1}^{2}]=\underline {\sigma }^{2}\), \(\hat {\mathbb {E}}[Y_{1}]=\overline {\mu }\), \(\widehat {\mathcal {E}}[Y_{1}]=\underline {\mu }\). Denote
with \(\hat {\mathbb {E}}[X_{1}]=\hat {\mathbb {E}}[-X_{1}]=0\), \(\hat {\mathbb {E}}[X_{1}^{2}]=\overline {\sigma }^{2}\), \(\widehat {\mathcal {E}}[X_{1}^{2}]=\underline {\sigma }^{2}\), \(\hat {\mathbb {E}}[Y_{1}]=\overline {\mu }\), \(\widehat {\mathcal {E}}[Y_{1}]=\underline {\mu }\). Denote
Let ξ be a G-normal distributed random variable, η be a maximal distributed random variable such that the distribution of (ξ,η) is characterized by the following parabolic partial differential equation (PDE) defined on \([0,\infty)\times \mathbb {R}\times \mathbb {R}\):
i.e., if for any bounded Lipschitz function \(\varphi (x,y):\mathbb {R}^{2}\rightarrow \mathbb {R}\), the function \(u(x,y,t)=\widetilde {\mathbb {E}}\left [\varphi \left (x+\sqrt {t} \xi, y+t\eta \right)\right ]\) (\(x,y \in \mathbb {R}, t\ge 0\)) is the unique viscosity solution of the PDE (13) with Cauchy condition u| t=0=φ.
Further, let B t and b t be two random processes such that the distribution of the process (B ·,b ·) is characterized by
-
(i)
B 0=0, b 0=0;
-
(ii)
for any 0≤t 1≤…≤t k ≤s≤t+s, (B s+t −B s ,b s+t −b s ) is independent to \((B_{t_{j}}, b_{t_{j}}), j=1,\ldots,k\), in sense that, for any \(\varphi \in C_{l,Lip}(\mathbb {R}^{2(k+1)})\),
$$ \begin{aligned} & \widetilde{\mathbb{E}}\left[\varphi\left((B_{t_{1}}, b_{t_{1}}),\ldots,(B_{t_{k}}, b_{t_{k}}), (B_{s+t}-B_{s}, b_{s+t}-b_{s})\right)\right]\\ &\qquad = \widetilde{\mathbb{E}}\left[\psi\left((B_{t_{1}}, b_{t_{1}}),\ldots,(B_{t_{k}}, b_{t_{k}})\right)\right], \end{aligned} $$(14)where
$$ \begin{aligned} \psi\left((x_{1}, y_{1}),\ldots,(x_{k}, y_{k})\right)= \widetilde{\mathbb{E}}\left[\varphi\left((x_{1}, y_{1}),\ldots,(x_{k}, y_{k})\right.\right.,\\ \left.\left.(B_{s+t}-B_{s}, b_{s+t}-b_{s})\right)\right]; \end{aligned} $$ -
(iii)
for any t,s>0, \((B_{s+t}-B_{s},b_{s+t}-b_{s})\overset {d}\sim (B_{t},b_{t})\) under \(\widetilde {\mathbb {E}}\);
-
(iv)
for any t>0, \((B_{t},b_{t})\overset {d}\sim \left (\sqrt {t}B_{1}, tb_{1}\right)\) under \(\widetilde {\mathbb {E}}\);
-
(v)
the distribution of (B 1,b 1) is characterized by the PDE (13).
It is easily seen that B t is a G-Brownian motion with \(B_{1}\sim N\left (0,[\underline {\sigma }^{2},\overline {\sigma }^{2}]\right)\), and (B t ,b t ) is a generalized G-Brownian motion introduced by Peng (2010a). The existence of the generalized G-Brownian motion can be found in Peng (2010a).
Theorem 4
Suppose \(\hat {\mathbb {E}}\left [(X_{1}^{2}-b)^{+}\right ]\rightarrow 0\) and \(\hat {\mathbb {E}}\left [(|Y_{1}|-b)^{+}\right ]\rightarrow 0\) as b→∞. Let
Then, for any bounded continuous function \(\varphi :C[0,1]\times C[0,1]\rightarrow \mathbb R\),
Further, let p≥2, q≥1, and assume \(\hat {\mathbb {E}}[|X_{1}|^{p}]<\infty \), \(\hat {\mathbb {E}}[|Y_{1}|^{q}]<\infty \). Then, for any continuous function \(\varphi :C[0,1]\times C[0,1]\rightarrow \mathbb R\) with |φ(x,y)|≤C(1+∥x∥p+∥y∥q),
Here ∥x∥= sup0≤t≤1|x(t)| for x∈C[0,1].
Remark 3
When X k and Y k are random vectors in \(\mathbb R^{d}\) with \(\hat {\mathbb {E}}[X_{k}]=\hat {\mathbb {E}}[-X_{k}]=0\), \(\hat {\mathbb {E}}[(\|X_{1}\|^{2}-b)^{+}]\rightarrow 0\) and \(\hat {\mathbb {E}}[(\|Y_{1}\|-b)^{+}]\rightarrow 0\) as b→∞. Then, the function G in (12) becomes
where \(\mathbb S(d)\) is the collection of all d×d symmetric matrices. The conclusion of Theorem 4 remains true with the distribution of (B 1,b 1) being characterized by the following parabolic partial differential equation defined on \([0,\infty)\times \mathbb {R}^{d}\times \mathbb {R}^{d}\):
where \(D_{y} =(\partial _{y_{i}})_{i=1}^{n}\) and \(D_{xx}^{2}=(\partial _{x_{i}x_{j}}^{2})_{i,j=1}^{d}\).
Remark 4
As a conclusion of Theorem 4, we have
This is proved by Peng (2010a) under the conditions \(\hat {\mathbb {E}}\left [\left |X_{1}\right |^{2+\delta }\right ]<\infty \) and \(\hat {\mathbb {E}}\left [|Y_{1}|^{1+\delta }\right ]<\infty \) (cf. Theorem 3.6 and Remark 3.8 therein).
When Y 1≡0, (15) becomes
which is proved by Zhang (2015).
Before the proof, we need several lemmas. For random vectors X
n
in  and X in
and X in  , we write \(\boldsymbol X_{n}\overset {d}\rightarrow \boldsymbol {X}\) if
, we write \(\boldsymbol X_{n}\overset {d}\rightarrow \boldsymbol {X}\) if
for any bounded continuous φ. Write \(\boldsymbol X_{n} \overset {\mathbb {V}}\rightarrow \boldsymbol {x}\) if \(\mathbb {V}(\|\boldsymbol {X}_{n}-\boldsymbol {x}\|\ge \epsilon)\rightarrow 0\) for any ε>0. {X n } is called uniformly integrable if
The following three lemmas are obvious.
Lemma 2
If \(\boldsymbol {X}_{n}\overset {d}\rightarrow \boldsymbol {X}\) and φ is a continuous function, then \(\varphi (\boldsymbol {X}_{n})\overset {d}\rightarrow \varphi (\boldsymbol {X})\).
Lemma 3
(Slutsky’s Lemma) Suppose \(\boldsymbol {X}_{n}\overset {d}\rightarrow \boldsymbol {X}\), \(\boldsymbol {Y}_{n} \overset {\mathbb {V}}\rightarrow \boldsymbol {y}\), \(\eta _{n}\overset {\mathbb {V}}\rightarrow a\), where a is a constant and y is a constant vector, and \(\widetilde {\mathbb {V}}(\|\boldsymbol {X}\|>\lambda)\rightarrow 0\) as λ→∞. Then, \((\boldsymbol {X}_{n}, \boldsymbol {Y}_{n}, \eta _{n})\overset {d}\rightarrow (\boldsymbol {X},\boldsymbol {y}, a)\), and as a result, \(\eta _{n}\boldsymbol {X}_{n}+\boldsymbol {Y}_{n}\overset {d}\rightarrow a\boldsymbol {X}+\boldsymbol {y}\).
Remark 5
Suppose \(\boldsymbol {X}_{n}\overset {d}\rightarrow \boldsymbol {X}\). Then, \(\widetilde {\mathbb {V}}(\|\boldsymbol {X}\|>\lambda)\rightarrow 0\) as λ→∞ is equivalent to the tightness of {X n ;n≥1}, i.e.,
because for all ε>0, we can define a continuous function φ(x) such that I{x>λ+ε}≤φ(x)≤I{x>λ] and so
Lemma 4
Suppose \(\boldsymbol {X}_{n}\overset {d}\rightarrow \boldsymbol {X}\).
-
(a)
If {X n } is uniformly integrable and \(\widetilde {\mathbb {E}}[((\|\boldsymbol {X}\|-b)^{+}]\rightarrow 0\) as b→∞, then,
$$ \hat{\mathbb{E}}[\boldsymbol{X}_{n}]\rightarrow \widetilde{\mathbb{E}}[\boldsymbol{X}]. $$(17) -
(b)
If \(\sup _{n}\hat {\mathbb {E}}[|\boldsymbol X_{n}\|^{q}<\infty \) and \(\widetilde {\mathbb {E}} [|\boldsymbol {X}\|^{q}<\infty \) for some q>1, then (17) holds.
The following lemma is proved by Zhang (2015).
Lemma 5
Suppose that \(\boldsymbol {X}_{n}\overset {d}\rightarrow \boldsymbol {X}\), \(\boldsymbol {Y}_{n}\overset {d}\rightarrow \boldsymbol {Y}\), Y n is independent to X n under \(\hat {\mathbb {E}}\) and \(\widetilde {\mathbb {V}}(\|\boldsymbol {X}\|>\lambda)\rightarrow 0\) and \(\widetilde {\mathbb {V}}(\|\boldsymbol {Y}\|>\lambda)\rightarrow 0\) as λ→∞. Then \( (\boldsymbol {X}_{n},\boldsymbol {Y}_{n})\overset {d}\rightarrow (\overline {\boldsymbol {X}},\overline {\boldsymbol {Y}}), \) where \(\overline {\boldsymbol {X}}\overset {d}=\boldsymbol {X}\), \(\overline {\boldsymbol {Y}}\overset {d}=\boldsymbol {Y}\) and \(\overline {\boldsymbol {Y}}\) is independent to \(\overline {\boldsymbol {X}}\) under \(\widetilde {\mathbb {E}}\).
The next lemma is about the Rosenthal-type inequalities due to Zhang (2016).
Lemma 6
Let {X
1,…,X
n
} be a sequence of independent random variables in  .
.
-
(a)
Suppose p≥2. Then,
$$ \begin{aligned} \hat{\mathbb{E}}\left[\max_{k\le n} \left|S_{k}\right|^{p}\right]&\le C_{p}\left\{ \sum_{k=1}^{n} \hat{\mathbb{E}} \left[|X_{k}|^{p}\right]+\left(\sum_{k=1}^{n} \hat{\mathbb{E}} \left[|X_{k}|^{2}\right]\right)^{p/2} \right. \\ & \qquad \left. +\left(\sum_{k=1}^{n} \left[\left(\widehat{\mathcal{E}} [X_{k}]\right)^{-}+\left(\hat{\mathbb{E}} [X_{k}]\right)^{+}\right]\right)^{p}\right\}. \end{aligned} $$(18) -
(b)
Suppose \(\hat {\mathbb {E}}[X_{k}]\le 0\), k=1,…,n. Then,
$$ \hat{\mathbb{E}}\left[\left|\max_{k\le n} (S_{n}-S_{k})\right|^{p}\right] \le 2^{2-p}\sum_{k=1}^{n} \hat{\mathbb{E}} [|X_{k}|^{p}], \;\; \text{for} 1\le p\le 2 $$(19)and
$$ \begin{aligned} \hat{\mathbb{E}}\left[\left|\max_{k\le n}(S_{n}- S_{k})\right|^{p}\right] &\le C_{p}\left\{ \sum_{k=1}^{n} \hat{\mathbb{E}} \left[|X_{k}|^{p}\right]+\left(\sum_{k=1}^{n} \hat{\mathbb{E}} \left[|X_{k}|^{2}\right]\right)^{p/2}\right\} \\ &\le C_{p} n^{p/2-1} \sum_{k=1}^{n} \hat{\mathbb{E}} [|X_{k}|^{p}], \;\; \text{for}~p\ge 2. \end{aligned} $$(20)
Lemma 7
Suppose \(\hat {\mathbb {E}}[X_{1}]=\hat {\mathbb {E}}[-X_{1}]=0\) and \(\hat {\mathbb {E}}\left [X_{1}^{2}\right ]<\infty \). Let \(\overline {X}_{n,k}=(-\sqrt {n})\vee X_{k}\wedge \sqrt {n}\), \(\widehat {X}_{n,k}=X_{k}-\overline {X}_{n,k}\), \(\overline {S}_{n,k}^{X}=\sum _{j=1}^{k} \overline {X}_{n,j}\) and \(\widehat {S}_{n,k}^{X}=\sum _{j=1}^{k}\widehat {X}_{n,j}\), k=1,…,n. Then
and
whenever \(\hat {\mathbb {E}}[(|X_{1}|^{p}-b)^{+}]\rightarrow 0\) as b→∞ if p=2, and \(\hat {\mathbb {E}}[|X_{1}|^{p}]<\infty \) if p>2.
Proof
Note \(\hat {\mathbb {E}}[X_{1}]=\widehat {\mathcal {E}}[X_{1}]=0\). So, \(|\widehat {\mathcal {E}}[\overline {X}_{n,1}]|=|\widehat {\mathcal {E}}[X_{1}]-\widehat {\mathcal {E}}[\overline {X}_{n,1}]|\le \hat {\mathbb {E}}|\widehat {X}_{n,1}|\le \hat {\mathbb {E}}[(|X_{1}|^{2}-n)^{+}]n^{-1/2}\) and \(|\hat {\mathbb {E}}[\overline {X}_{n,1}]|=|\hat {\mathbb {E}}[X_{1}]-\hat {\mathbb {E}}[\overline {X}_{n,1}]|\le \hat {\mathbb {E}}|\widehat {X}_{n,1}|\le \hat {\mathbb {E}}[(|X_{1}|^{2}-n)^{+}]n^{-1/2}\). By Rosenthal’s inequality (cf. (18)),
and
The proof is completed. □
Lemma 8
(a) Suppose p≥2, \(\hat {\mathbb {E}}[X_{1}]=\hat {\mathbb {E}}[-X_{1}]=0\), \(\hat {\mathbb {E}}[(X_{1}^{2}-b)^{+}]\rightarrow 0\) as b→∞ and \(\hat {\mathbb {E}}[|X_{1}|^{p}]<\infty \). Then,
(b) Suppose p≥1, \(\hat {\mathbb {E}}\left [(|Y_{1}|-b)^{+}\right ]\rightarrow 0\) as b→∞, and \(\hat {\mathbb {E}}[|Y_{1}|^{p}]<\infty \). Then,
Proof
(a) follows from Lemma 6. (b) is obvious by noting
by the Rosenthal-type inequalities (19) and (20). □
Lemma 9
Suppose \(\hat {\mathbb {E}}\left [(|Y_{1}|-b)^{+}\right ]\rightarrow 0\) as b→∞. Then, for any ε>0,
Proof
Let Y k,b =(−b)∨Y k ∧b, \(S_{n,1}=\sum _{k=1}^{n} Y_{k,b}\) and \(S_{n,2}=S_{n}^{Y}-S_{n,1}\). Note \(\hat {\mathbb {E}}\big [Y_{1,b}]\rightarrow \hat {\mathbb {E}}[Y_{1}]\) as b→∞. Suppose \(\left |\hat {\mathbb {E}}[Y_{1,b}] - \hat {\mathbb {E}}[Y_{1}]\right |<\epsilon /4\). Then, by Kolmogorov’s inequality (cf. (19)),
Also,
It follows that
By considering {−Y k } instead, we have
□
Proof of Theorem 4.
We first show the tightness of \(\widetilde {\boldsymbol W}_{n}\). It is easily seen that
It follows that for any ε>0, if δ<ε/(4b), then
Letting δ→0 and then b→∞ yields
For any η>0, we choose δ k ↓0 such that, if
then \(\sup _{n}\mathbb {V}\left (\widetilde {S}_{n}^{Y}(\cdot)/n \in A_{k}^{c}\right)\le \eta /2^{k+1}\). Let A={x:|x(0)|≤a}, \(K_{2}=A\bigcap _{k=1}^{\infty }A_{k}\). Then, by the Arzelá-Ascoli theorem, K 2⊂C b (C[0,1]) is compact. It is obvious that \(\{ \widetilde {S}_{n}^{Y}(\cdot)/n\not \in A\}=\emptyset \), because \( \widetilde {S}_{n}^{Y}(0)/n=0\). Next, we show that
Note that when δ<1/(2n),
Choose a k 0 such that δ k <1/(2Mk) for k≥k 0. Then, on the event E={maxi≤n|Y i |≤M}, \(\{ \widetilde {S}_{n}^{Y}(\cdot)/n\in A_{k}^{c}\}=\emptyset \) for k≥k 0. So, by the (finite) sub-additivity of \(\mathbb {V}\),
On the other hand,
It follows that
Letting M→∞ yields
We conclude that for any η>0, there exists a compact K 2⊂C b (C[0,1]) such that
Next, we show that for any η>0, there exists a compact K 1⊂C b (C[0,1]) such that
Similar to (21), it is sufficient to show that
With the same argument of Billingsley (1968, Pages 56–59, cf. (8.12)), for large n,
It follows that
by Lemma 8 (a), where p=2. On the other hand, for fixed n, if δ<1/(2n), then
We have
for each n. It follows that (23) holds.
Now, by combining (21) and (22) we obtain the tightness of \(\widetilde {\boldsymbol W}_{n}\) as follows.
Define \(\hat {\mathbb {E}}_{n}\) by
Then, the sequence of sub-linear expectations \(\{\hat {\mathbb {E}}_{n}\}_{n=1}^{\infty }\) is tight by (24). By Theorem 9 of Peng (2010b), \(\{\hat {\mathbb {E}}_{n}\}_{n=1}^{\infty }\) is weakly compact, namely, for each subsequence \(\{\hat {\mathbb {E}}_{n_{k}}\}_{k=1}^{\infty }\), n k →∞, there exists a further subsequence \(\left \{\hat {\mathbb {E}}_{m_{j}}\right \}_{j=1}^{\infty } \subset \left \{\hat {\mathbb {E}}_{n_{k}}\right \}_{k=1}^{\infty }\), m j →∞, such that, for each φ∈C b (C[0,1]×C[0,1]), \(\{\hat {\mathbb {E}}_{m_{j}}[\varphi ]\}\) is a Cauchy sequence. Define \({\mathbb F}[\cdot ]\) by
Let \(\overline {\Omega }=C[0,1]\times C[0,1]\), and (ξ t ,η t ) be the canonical process \(\xi _{t}(\omega) = \omega _{t}^{(1)}\), \(\eta _{t}(\omega)=\omega _{t}^{(2)}\left (\omega =\left (\omega ^{(1)},\omega ^{(2)}\right)\in \overline {\Omega }\right)\). Then,
The topological completion of \(C_{b}(\overline {\Omega })\) under the Banach norm \({\mathbb F}[\|\cdot \|]\) is denoted by \(L_{\mathbb F} (\overline {\Omega })\). \({\mathbb F}[\cdot ]\) can be extended uniquely to a sub-linear expectation on \(L_{\mathbb F} (\overline {\Omega })\).
Next, it is sufficient to show that (ξ t ,η t ) defined on the sub-linear space \((\overline {\Omega }, L_{\mathbb F} (\overline {\Omega }), {\mathbb F})\) satisfies (i)-(v) and so \((\xi _{\cdot },\eta _{\cdot })\overset {d}=(B_{\cdot },b_{\cdot })\), which means that the limit distribution of any subsequence of \(\widetilde {\boldsymbol W}_{n}(\cdot)\) is uniquely determined.
The conclusion in (i) is obvious. For (ii) and (iii), we let 0≤t 1≤…≤t k ≤s≤t+s. By (25), for any bounded continuous function \(\varphi :\mathbb R^{2(k+1)}\rightarrow \mathbb R\) we have
Note
It follows that by Lemmas 3 and 8,
In particular,
It follows that
On the other hand,
by (26). Hence,
Next, we show that
By Lemma 9,
It follows that
For considering ξ s+t −ξ s , we let \(\overline {S}_{n,k}^{X}\) and \(\widehat {S}_{n,k}^{X}\) be defined as in Lemma 7. Then, \(S_{k}^{X}=\overline {S}_{n,k}^{X}+ \widehat {S}_{n,k}^{X}\). By (27) and Lemmas 7 and 3,
It follows that
Hence,
by the completeness of \((\overline {\Omega }, L_{\mathbb F} (\overline {\Omega }), {\mathbb F})\). (29) is proved.
Now, note that (X i ,Y i ),i=1,2,…, are independent and identically distributed. By (26) and Lemma 5, it is easily seen that (ξ ·,η ·) satisfies (14) for \(\varphi \in C_{b}(\mathbb R^{2(k+1)})\). Note that, by (29), the random variables concerned in (14) and (28) have finite moments of each order. The function space \(C_{b}(\mathbb R^{2(k+1)})\) and \(C_{b}(\mathbb R^{2})\) can be extended to \(C_{l,Lip}(\mathbb R^{2(k+1)})\) and \(C_{l,Lip}(\mathbb R^{2})\), respectively, by elemental arguments. So, (ii) and (iii) are proved.
For (iv) and (v), we let \(\varphi :\mathbb R^{2}\rightarrow \mathbb R\) be a bounded Lipschitz function and consider
It is sufficient to show that u is a viscosity solution of the PDE (13). In fact, due to the uniqueness of the viscosity solution, we will have
Letting x=0 and y=0 yields (iv) and (v).
To verify PDE (13), first it is easily seen that
Note that \(\left \{\frac {q}{2} \left (\frac {S_{[nt]}^{X}}{\sqrt {n}}\right)^{2}+p \frac {S_{[nt]}^{Y}}{n}\right \}\) is uniformly integrable by Lemma 8. By Lemma 4, we conclude that
It is obvious that if q 1≤q 2, then G(p,q 1)−G(p,q 2)≤G(0,q 1−q 2)≤0. Also, it is easy to verify that \( |u(x,y,t)-u(\overline {x},\overline {y},t)|\le C (|x-\overline {x}|+|y-\overline {y}|) \), \( |u(x,y,t)-u(x,y,s)|\le C\sqrt {|t-s|}\) by the Lipschitz continuity of φ, and
Let \(\psi (\cdot,\cdot,\cdot)\in C_{b}^{3,3,2}(\mathbb R,\mathbb R,[0,1])\) be a smooth function with ψ≥u and ψ(x,y,t)=u(x,y,t). Then,
where
By (29), we have \( {\mathbb F}[|I_{s}|]\le C\big (s^{3/2}+s^{2}+s^{2}\big)=o(s). \) It follows that \([\partial _{t} \psi - G(\partial _{y}\psi,\partial _{xx}^{2})](x,y,t)\le 0\). Thus, u is a viscosity subsolution of (13). Similarly, we can prove that u is a viscosity supersolution of (13). Hence, (15) is proved.
As for (16), let \(\varphi :C[0,1]\times C[0,1]\rightarrow \mathbb R\) be a continuous function with |φ(x,y)|≤C 0(1+∥x∥p+∥y∥q). For λ>4C 0, let φ λ (x,y)=(−λ)∨(φ(x,y)∧λ)∈C b (C[0,1]). It is easily seen that φ(x,y)=φ λ (x,y) if |φ(x,y)|≤λ. If |φ(x,y)|>λ, then
Hence,
It follows that
by Lemma 8. Further, by (15),
(16) is proved, and the proof of Theorem 4 is now completed. □
Proof of Theorem 4.
When X k and Y k are d-dimensional random vectors, the tightness (24) of \(\widetilde {\boldsymbol W_{n}}(\cdot)\) also follows, because each sequence of the components of vector \(\widetilde {\boldsymbol W_{n}}(\cdot)\) is tight. Also, (29) remains true, because each component has this property. Moreover, it follows that
The remaining proof is the same as that of Theorem 4. □
Proof of the self-normalized FCLTs
Let \(Y_{k}=X_{k}^{2}\). The function G(p,q) in (12) becomes
Then, the process (B t ,b t ) in (15) and the process (W(t),〈W〉 t ) are identically distributed.
In fact, note
It is easy to verify that (W(t),〈W〉 t ) satisfies (i)-(iv) for (B ·,b ·). It remains to show that \((B_{1}, b_{1})\overset {d}= (W(1), \langle W\rangle _{1})\). Let {X n ;n≥1} be a sequence of independent and identically distributed random variables with \(X_{1}\overset {d}= W(1)\). Then, by Theorem 4,
Further, let \(t_{k}=\frac {k}{n}\). Then,
Hence, \((B_{\cdot },b_{\cdot })\overset {d}=(W(\cdot), \langle W\rangle _{\cdot })\). We conclude the following proposition from Theorem 4.
Proposition 1
Suppose \(\hat {\mathbb {E}}[(X_{1}^{2}-b)^{+}]\rightarrow 0\) as b→∞. Then, for any bounded continuous function \(\psi :C[0,1]\times C[0,1]\rightarrow \mathbb R\),
where \(\widetilde {V}_{n}(t)=V_{[nt]}+(nt-[nt])X^{2}_{[nt]+1}\), and, in particular, for any bounded continuous function \(\psi :C[0,1]\times \mathbb R\rightarrow \mathbb R\),
Now, we begin the proof of Theorem 2. Let \(a=\underline {\sigma }^{2}/2\) and \(b=2\overline {\sigma }^{2}\). According to (30), we have \(\widetilde {\mathcal {V}}\big (\underline {\sigma }^{2}-\epsilon < \langle W \rangle _{1}<\overline {\sigma }^{2}+\epsilon \big)=1\) for all ε>0. Let \(\varphi :C[0,1]\rightarrow \mathbb R\) be a bounded continuous function. Define
Then, \(\psi :C[0,1]\times \mathbb R\rightarrow \mathbb R\) is a bounded continuous function. Hence, by Proposition 1,
Also,
It follows that
The proof is now completed. □
Proof of Theorem 3.
First, note that
The condition (I) implies that l(x) is slowly varying as x→∞ and
Further,
If conditions (I) and (III) are satisfied, then
Now, let d t = inf{x:x −2 l(x)=t −1}. Then, \(nl(d_{n})=d_{n}^{2}\). Similar to Theorem 2, it is sufficient to show that for any bounded continuous function \(\psi :C[0,1]\times C[0,1]\rightarrow \mathbb R\),
Let \(\overline {X}_{k}=\overline {X}_{k,n}=(-d_{n})\vee X_{k}\wedge d_{n}\), \(\overline {S}_{k} =\sum _{i=1}^{k} \overline {X}_{i}\), \(\overline {V}_{k}=\sum _{i=1}^{k} \overline {X}_{i}^{2}\). Denote \( \overline {S}_{n}(t)=\overline {S}_{[nt]}+(nt-[nt])\overline {X}_{[nt]+1}\) and \(\overline {V}_{n}(t)=\overline {V}_{[nt]}+(nt-[nt])\overline {X}^{2}_{[nt]+1}\). Note
It is sufficient to show that for any bounded continuous function \(\psi :C[0,1]\times C[0,1]\rightarrow \mathbb R\),
Following the line of the proof of Theorem 4, we need only to show that
-
(a)
for any 0<t≤1,
$${} \limsup_{n\rightarrow \infty} \hat{\mathbb{E}}\left[\max_{k\le [nt]}\left|\frac{\overline{S}_{k}}{d_{n}}\right|^{p}\right]\le C_{p} t^{p/2},\;\; \limsup_{n\rightarrow \infty}\hat{\mathbb{E}}\left[\max_{k\le [nt]}\left|\frac{\overline{V}_{k}}{d_{n}^{2}}\right|^{p}\right]\le C_{p} t^{p},\;\; \forall p\ge 2; $$ -
(b)
for any 0<t≤1,
$$ {\lim}_{n\rightarrow \infty} \hat{\mathbb{E}}\left[ \frac{q}{2} \left(\frac{\overline{S}_{[nt]}}{d_{n}}\right)^{2}+p \frac{\overline{V}_{[nt]}}{d_{n}^{2}}\right]=tG(p,q), $$where
$$G(p,q)=\left(\frac{q}{2}+p\right)^{+} - r^{-2}\left(\frac{q}{2}+p\right)^{-}; $$ -
(c)
$${\kern-3.8cm} \max_{k\le n} \frac{|X_{k}|}{d_{n}}\overset{\mathbb{V}}\rightarrow 0. $$
In fact, (a) implies the tightness of \(\left (\frac {\widetilde {S}_{n}^{X}(\cdot)}{d_{n}},\frac {\widetilde {V}_{n}(\cdot)}{d_{n}^{2}}\right)\) and (29), and (b) implies the distribution of the limit process is uniquely determined.
First, (c) is obvious, because
As for (a), by the Rosenthal-type inequality (18),
and similarly,
Thus (a) follows.
As for (b), note
By (32),
and similarly,
Further,
and
Hence, we conclude that
Thus, (b) is statisfied, and the proof is completed. □
References
Csörgő, M, Szyszkowicz, B, Wang, QY: Donsker’s theorem for self-normalized partial sums processes. Ann. Probab. 31, 1228–1240 (2003).
Denis, L, Hu, MS, Peng, SG: Function spaces and capacity related to a sublinear expectation: application to G-Brownian Motion Paths. Potential Anal. 34, 139–161 (2011). arXiv:0802.1240v1 [math.PR].
Giné, E, Götze, F, Mason, DM: When is the Student t-statistic asymptotically standard normal?. Ann. Probab. 25, 1514–1531 (1997).
Hu, MS, Ji, SL, Peng, SG, Song, YS: Backward stochastic differential equations driven by G-Brownian motion. Stochastic Process. Appl. 124(1), 759–784 (2014a).
Hu, MS, Ji, SL, Peng, SG, Song, YS: Comparison theorem, Feynman-Kac formula and Girsanov transformation for BSDEs driven by G-Brownian motion. Stochastic Process. Appl. 124(2), 1170–1195 (2014b).
Li, XP, Peng, SG: Topping times and related Ito’s calculus with G-Brownian motion. Stochastic Process. Appl. 121(7), 1492–1508 (2011).
Nutz, M, van Handel, R: Constructing sublinear expectations on path space. Stochastic Process. Appl. 123(8), 3100–3121 (2013).
Peng, SG: G-expectation, G-Brownian motion and related stochastic calculus of Ito’s type. In: The Abel Symposium 2005, Abel Symposia 2, Edit. Benth et. al, pp. 541–567. Springer-Verlag (2006).
Peng, SG: Multi-dimensional G-Brownian motion and related stochastic calculus under G-expectation. Stochastic Process. Appl. 118(12), 2223–2253 (2008a).
Peng, SG: A new central limit theorem under sublinear expectations (2008b). Preprint: arXiv:0803.2656v1 [math.PR].
Peng, SG: Survey on normal distributions, central limit theorem, Brownian motion and the related stochastic calculus under sublinear expectations. Sci. China Ser. A. 52(7), 1391–1411 (2009).
Peng, SG: Nonlinear Expectations and Stochastic Calculus under Uncertainty (2010a). Preprint: arXiv:1002.4546 [math.PR].
Peng, SG: Tightness, weak compactness of nonlinear expectations and application to CLT (2010b). Preprint: arXiv:1006.2541 [math.PR].
Yan, D, Hutz, M, Soner, HM: Weak approximation of G-expectations. Stochastic Process. Appl. 122(2), 664–675 (2012).
Zhang, LX: Donsker’s invariance principle under the sub-linear expectation with an application to Chung’s law of the iterated logarithm. Commun. Math. Stat. 3(2), 187–214 (2015). arXiv:1503.02845 [math.PR].
Zhang, LX: Rosenthal’s inequalities for independent and negatively dependent random variables under sub-linear expectations with applications. Sci. China Math. 59(4), 751–768 (2016).
Acknowledgments
Research supported by Grants from the National Natural Science Foundation of China (No. 11225104), the 973 Program (No. 2015CB352302) and the Fundamental Research Funds for the Central Universities.
Authors’ contributions
All authors have equal contributions to the paper. All authors read and approved the final manuscript.
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License(http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Lin, Z., Zhang, LX. Convergence to a self-normalized G-Brownian motion. Probab Uncertain Quant Risk 2, 4 (2017). https://doi.org/10.1186/s41546-017-0013-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41546-017-0013-8
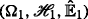 and
and 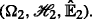 . They are called identically distributed, denoted by
. They are called identically distributed, denoted by  , a random vector
, a random vector 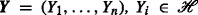 is said to be independent to another random vector
is said to be independent to another random vector 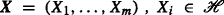 under
under