- Research
- Open access
- Published:
Pathwise no-arbitrage in a class of Delta hedging strategies
Probability, Uncertainty and Quantitative Risk volume 1, Article number: 3 (2016)
Abstract
We consider a strictly pathwise setting for Delta hedging exotic options, based on Föllmer’s pathwise Itô calculus. Price trajectories are d-dimensional continuous functions whose pathwise quadratic variations and covariations are determined by a given local volatility matrix. The existence of Delta hedging strategies in this pathwise setting is established via existence results for recursive schemes of parabolic Cauchy problems and via the existence of functional Cauchy problems on path space. Our main results establish the nonexistence of pathwise arbitrage opportunities in classes of strategies containing these Delta hedging strategies and under relatively mild conditions on the local volatility matrix.
Introduction
In mainstream finance, the price evolution of a risky asset is usually modeled as a stochastic process defined on some probability space and hence is subject to model uncertainty. In a number of situations, however, it is possible to construct continuous-time strategies on a path-by-path basis and without making any probabilistic assumptions on the asset price evolution. A theory of hedging European options of the form H=h(S(T)) for one-dimensional asset price trajectories S=(S(t))0≤t≤T was developed by Bick and Willinger (1994) by using Föllmer’s (1981) approach to pathwise Itô calculus. Bick and Willinger (1994) showed, in particular, that if S is strictly positive and admits a pathwise quadratic variation of the form \({\langle }S,S{\rangle }(t)={\int _{0}^{t}}a(s,S(s)){\,\mathrm {d}} s\) for some function a(s,x)>0, then a solution v to the terminal-value problem
is such that v(t,S(t)) is the portfolio value of a self-financing trading strategy that perfectly replicates the option H=h(S(T)) in a strictly pathwise sense. In particular, the amount v(0,S(0)) can be regarded as the cost required to hedge the option H. In continuous-time finance, this amount is usually equated with an arbitrage-free price of H. The latter interpretation, however, is not clear in the pathwise situation, because one first needs to exclude the existence of arbitrage in a strictly pathwise sense.
In the present paper we pick up the approach from (Bick and Willinger 1994) and, in a first step, extend their results to a setting with a d-dimensional price trajectory, S(t)=(S 1(t),…,S d (t))⊤, and an exotic derivative of the form H=h(S(t 0),…,S(t N )), where t 0<t 1<⋯<t N are the fixing times of daily closing prices and h is a certain function. In practice, most exotic derivatives that pay off at maturity (i.e., European-style) are of this form. Using ideas from (Schied and Stadje 2007), we show that such options can be hedged in a strictly pathwise sense if a certain recursive scheme of terminal-value problems (1.1) can be solved, and we provide sufficient conditions for the existence and uniqueness of the corresponding solutions.
In the second part of the paper we then approach the absence of strictly pathwise arbitrage within a class of strategies that are based on solutions of recursive schemes of terminal-value problems. This class of strategies hence includes, in particular, the Delta hedging strategies of exotic derivatives of the form H=h(S(t 0),…,S(t N )). Our main result, Theorem 3.3, states that there are no admissible arbitrage opportunities as soon as the covariation of the price trajectory is of the form
and the matrix a(t,x)=(a ij (t,x)) is continuous, bounded, and positive definite. Here, admissibility refers to the usual requirement that the portfolio value of a strategy must be bounded from below for all considered price trajectories.
Our result on the absence of arbitrage is related to (Alvarez et al. 2013, Theorem 4), where the absence of pathwise arbitrage is established for d=1, a>0 constant, and a certain class of smooth strategies. There are, however, several differences between this and our result. First, we consider a more general class of price trajectories that are based on local instead of constant volatility, allow for an arbitrary number d of traded assets, and may either be strictly positive or of the Bachelier type. Second, our class of trading strategies comprises the natural Delta hedging strategies for path-dependent exotic options and, third, we use a completely different approach to prove our result; while Alvarez et al. (2013) use a continuity argument to transfer the absence of arbitrage from the probabilistic Black–Scholes model to a pathwise context, our proof does not rely on any probabilistic asset pricing model. Instead, we use Stroock’s and Varadhan’s (1972) idea for a probabilistic proof of Nirenberg’s strong parabolic maximum principle.
We then consider a setup, in which an option’s payoff may depend on the full trajectory of asset prices. In this functional framework, Föllmer’s pathwise Itô formula needs to be replaced by its functional extension, which was formulated by Dupire (2009) and further developed by Cont and Fournié (2010). Furthermore, the Cauchy problem (1.1) (and the corresponding iterated scheme) need to be replaced by a functional Cauchy problem on path space as studied in Peng and Wang (2016) and Ji and Yang (2013). We provide versions of our results on hedging strategies and the absence of pathwise arbitrage also in this functional setting.
There are many other approaches to hedging and arbitrage in the face of model risk. For continuous-time results, see, for instance, Lyons (1995), Hobson (2011; 1998), Vovk (2011; 2012; 2015), Bender et al. (2008), Davis et al. (2014), Biagini et al. (2015), Beiglböck et al. (2015), Schied et al. (2016), and the references therein. Discrete-time settings were, for instance, considered in Acciaio et al. (2016), Bouchard and Nutz (2015), Föllmer and Schied (2011), Riedel (2015), and again the references therein.
This paper is organized as follows. In Section “Strictly pathwise hedging of exotic derivatives”, we introduce a general framework for continuous-time trading by means of Föllmer’s pathwise Itô calculus. Based on an extension of an argument from (Föllmer 2001), our Proposition 2.1 will, in particular, justify the assumption that price trajectories should admit pathwise quadratic variations and covariations. We will then introduce the pathwise framework for hedging exotic options à la Bick and Willinger (1994). In Section “Absence of pathwise arbitrage”, we will introduce the class of strategies to which our no-arbitrage result, Theorem 3.3, applies. The extension to the functional setting is given in Section “Extension to functionally dependent strategies”. All proofs are contained in Section “Proofs”.
Strictly pathwise hedging of exotic derivatives
Pathwise Itô calculus can be used to model financial markets without probabilistic assumptions on the underlying asset price dynamics; see, e.g., (Bender et al. 2008; Bick and Willinger 1994; Davis et al. 2014; Föllmer 2001; Lyons 1995; Schied 2014; Schied and Stadje 2007; Schied et al. 2016) for corresponding case studies. In this section, we first motivate and describe a general setting for such an approach to asset price modeling and to the hedging of derivatives. Let us assume that we wish to trade continuously in d+1 assets. The first is a riskless bond, B(t), of which we assume for simplicity that it is of the form B(t)=1 for all t. This assumption can be justified by assuming that we are dealing here only with properly discounted asset prices. The prices of the d risky assets will be described by continuous functions S 1(t),…,S d (t), where the time parameter t varies over a certain time interval [ 0,T]. Throughout this paper, we will use vector notation such as S(t)=(S 1(t),…,S d (t))⊤. For the moment, when S=(S(t))0≤t≤T is fixed, a trading strategy will consist of a pair of functions ξ=(ξ 1,…,ξ d )⊤ and η, where ξ i (t) describes the number of shares held at time t in the i th risky asset and η(t) does the same for the riskless asset. The portfolio value of (ξ(t),η(t)) is then given as
where x·y denotes the euclidean inner product of two vectors x and y.
A key concept of mathematical finance is the notion of a self-financing trading strategy. If trading is only possible at finitely many times 0=t 0<t 1<⋯<t N <T, then ξ and η will be constant on each interval [t i ,t i+1) and on [t N ,T]. In this case it is well-known from discrete-time mathematical finance that the trading strategy (ξ,η) is self-financing if and only if
By making the mesh of the partition {t 0,…,t N } finer and finer, the Riemann sums on the right-hand side of (2.2) should converge to corresponding integrals, \({\int _{0}^{t}}\boldsymbol {\xi }(s){\,\mathrm {d}} \mathbf {S}(s)\) and \({\int _{0}^{t}}\eta (s){\,\mathrm {d}} B(s)\). Clearly, \({\int _{0}^{t}}\eta (s){\,\mathrm {d}} B(s)\) is a Riemann-Stieltjes integral, and criteria for its existence are well known. For a very specific class of strategies ξ, the following proposition gives necessary and sufficient conditions for the existence of \({\int _{0}^{t}}\boldsymbol {\xi }(s){\,\mathrm {d}} \mathbf {S}(s)\). This proposition extends and elaborates an argument by Föllmer (2001). Before stating this proposition, let us fix for the remainder of this paper a refining sequence of partitions, \(({\mathbb {T}}_{n})_{n\in {\mathbb {N}}}\). That is, each \({\mathbb {T}}_{n}\) is a finite partition of the interval [ 0,T], and we have \({\mathbb {T}}_{1}\subset {\mathbb {T}}_{2}\subset \cdots \) and the mesh of \({\mathbb {T}}_{n}\) tends to zero as n ↑ ∞. Moreover, it will be convenient to denote the successor of \(t\in {\mathbb {T}}_{n}\) by t ′. That is,
Proposition 2.1.
Let \(t\mapsto \mathbf {S}(t)\in {\mathbb {R}}^{d}\) be a continuous function on [ 0,T]. For i,j∈{1,…,d} and \(K_{ij}\in {\mathbb {R}}\) with K ij =K ji , we define the trading strategy \(\boldsymbol {\xi }^{ij}= \left (\xi ^{ij}_{1},\dots,\xi ^{ij}_{d}\right)^{\top }\) through
Then \({\int _{0}^{t}}\boldsymbol {\xi }^{ij}(s)\,\mathrm {d} \mathbf {S}(s)\)exists for all t and all i,j as the finite limit of the corresponding Riemann sums, i.e.,
if and only if the covariations,
exist in \({\mathbb {R}}\) for all t and all i,j. In this case it follows that
and, for i≠j,
The preceding proposition has the following two complementary implications.
-
If one wishes to deal with the very simple strategies of the form (2.3), then one must necessarily assume that the components of the asset price trajectory S admit all pathwise quadratic variations and covariations of the form (2.5).
-
Suppose that the quadratic variation of S i exists and vanishes identically. This is, for instance, the case if S i is Hölder continuous for some exponent α>1/2. Then, for ξ ii as in (2.3) and K ii =S i (0), the integral \({\int _{0}^{t}}\boldsymbol {\xi }(s){\,\mathrm {d}} \mathbf {S}(s)\) exists for all t. By letting \(\eta (t):={\int _{0}^{t}}\boldsymbol {\xi }(s){\,\mathrm {d}} \mathbf {S}(s)-\boldsymbol {\xi }^{\mathbf {S}}(t)\cdot \mathbf {S}(t)\), we obtain a self-financing trading strategy whose portfolio value is given by V(t)=(S i (t)−S i (0))2. But this is clearly an arbitrage opportunity as soon as S i is not constant. Hence, price trajectories of a risky asset necessarily need to be modeled by functions with nonvanishing quadratic variation.
These two aspects imply that it is reasonable to require that price trajectories S of a risky asset possess all covariations 〈S i ,S j 〉 in the sense that the limit in (2.5) exists for all t∈ [ 0,T]. It was shown by Föllmer (1981) that, if in addition the covariations are continuous functions of t, Itô’s formula holds in a strictly pathwise sense (see also (Sondermann 2006) for additional background and an English translation of (Föllmer 1981)). Let us thus denote by Q V d the class of all continuous functions \(\mathbf {S}:[\!0,T]\to {\mathbb {R}}^{d}\) on [ 0,T] for which all covariations 〈S i ,S j 〉(t) exist along \(({\mathbb {T}}_{n})\) and are continuous functions of t. We point out that the existence and the value of the covariation 〈S i ,S j 〉(t), and hence the space Q V d, depend in an essential manner on the choice of the refining sequence of partitions, \((\mathbb {T}_{n})\); see, e.g., (Freedman 1983, p. 47). Moreover, Q V d is not a vector space (Schied 2016). It follows easily from Föllmer’s pathwise Itô formula that for the following class of “basic admissible integrands” ξ, the Itô integral \({\int _{r}^{t}}\boldsymbol {\xi }(s){\,\mathrm {d}}\mathbf {S}(s)\) exists for all t∈ [ r,u]⊂ [ 0,T] as the finite limit of Riemann sums in (2.4); see (Schied 2014, p. 86). This integral is sometimes also called the Föllmer integral.
Definition 2.2. (Basic admissible integrands)
For 0≤r<u≤T, an \({\mathbb {R}}^{d}\)-valued function [ r,u]∋t↦ξ(t) is called a basic admissible integrand for S∈Q V d, if there exist \(m\in {\mathbb {N}}\), a continuous function \(\mathbf {A}:[\!r,u]\to {\mathbb {R}}^{m}\) whose components are functions of bounded variation, an open set \(O\subset {\mathbb {R}}^{m}\times {\mathbb {R}}^{d}\) such that (A(t),S(t))∈O for all t, and a continuously differentiable function \(f:O\to {\mathbb {R}}\) for which the function x→f(A(t),x) is for all t twice continuously differentiable on its domain, such that
where ∇ x f(a,x) denotes the gradient of x→f(a,x).
Following Bick and Willinger (1994), we will from now on consider not just one particular price trajectory S, but admit an entire class  of such trajectories so as to account for the uncertainty of the actual realization of the price trajectory. Specifically, we will consider the classes
of such trajectories so as to account for the uncertainty of the actual realization of the price trajectory. Specifically, we will consider the classes

and

where a(t,x)=(a
ij
(t,x))
i,j=1,…,d
is a continuous function of \((t,\mathbf {x})\in \,[\!0,T]\times {\mathbb {R}}^{d}\) (respectively of \((t,\mathbf {x})\in [0,T]\times {\mathbb {R}}_{+}^{d}\) in case of  ) into the set of positive definite symmetric d×d-matrices. Additional assumptions on a(t,x) will be formulated later on. Here, \({\mathbb {R}}_{+}:=(0,\infty)\), and we will write \({\mathbb {R}}^{d}_{(+)}\) to denote the two possibilities, \({\mathbb {R}}^{d}\) and \({\mathbb {R}}^{d}_{+}\), according to whether we are considering
) into the set of positive definite symmetric d×d-matrices. Additional assumptions on a(t,x) will be formulated later on. Here, \({\mathbb {R}}_{+}:=(0,\infty)\), and we will write \({\mathbb {R}}^{d}_{(+)}\) to denote the two possibilities, \({\mathbb {R}}^{d}\) and \({\mathbb {R}}^{d}_{+}\), according to whether we are considering  or
or  . Similarly, we will write
. Similarly, we will write  etc. Price trajectories in
etc. Price trajectories in  can arise as sample paths of multi-dimensional local volatility models. At least for d=1, the local volatility function \(\sigma (\cdot):=\sqrt {a(\cdot)}\) is often chosen by calibrating to the market prices of liquid plain vanilla options (Dupire 1997). Since in practice there are only finitely many given options prices, σ(·) is typically only determined on a finite grid (Bühler 2015), and so regularity assumptions on σ(·) can be made without loss of generality.
can arise as sample paths of multi-dimensional local volatility models. At least for d=1, the local volatility function \(\sigma (\cdot):=\sqrt {a(\cdot)}\) is often chosen by calibrating to the market prices of liquid plain vanilla options (Dupire 1997). Since in practice there are only finitely many given options prices, σ(·) is typically only determined on a finite grid (Bühler 2015), and so regularity assumptions on σ(·) can be made without loss of generality.
Our next goal is to introduce and characterize a class of self-financing trading strategies that may depend on the current value of the particular realization  and includes candidates for hedging strategies of European derivatives. Before that, let us introduce some notation. By C(D) we will denote the class of real-valued continuous functions on a set \(D\subset {\mathbb {R}}^{n}\). For an interval I⊂[0,T] with nonempty interior,
and includes candidates for hedging strategies of European derivatives. Before that, let us introduce some notation. By C(D) we will denote the class of real-valued continuous functions on a set \(D\subset {\mathbb {R}}^{n}\). For an interval I⊂[0,T] with nonempty interior,  , we denote by \(C^{1,2}\left (I\times {\mathbb {R}}^{d}_{(+)}\right)\) the class of all functions in \(C\left (I\times {\mathbb {R}}^{d}_{(+)}\right)\) that are continuously differentiable in
, we denote by \(C^{1,2}\left (I\times {\mathbb {R}}^{d}_{(+)}\right)\) the class of all functions in \(C\left (I\times {\mathbb {R}}^{d}_{(+)}\right)\) that are continuously differentiable in  , twice continuously differentiable in x for all
, twice continuously differentiable in x for all  , and whose derivatives admit continuous extensions to \(I\times {\mathbb {R}}^{d}_{(+)}\). Let us also introduce the following second-order differential operators,
, and whose derivatives admit continuous extensions to \(I\times {\mathbb {R}}^{d}_{(+)}\). Let us also introduce the following second-order differential operators,

Proposition 2.3.
Suppose that 0≤r<u≤T and that \(v\in C^{1,2}\left ([\!r,u]\times {\mathbb {R}}^{d}_{(+)}\right)\). Then the following conditions are equivalent.
-
(a)
For each
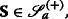 , there exists a basic admissible integrand ξ
S on [ r,u] such that
$$v(t,\mathbf{S}(t))=v(r,\mathbf{S}(r))+{\int_{r}^{t}}\boldsymbol{\xi}^{\mathbf{S}}(s)\,\,\mathrm{d} \mathbf{S}(s)\qquad\text{for \(t\in\,[r,u]\).} $$
, there exists a basic admissible integrand ξ
S on [ r,u] such that
$$v(t,\mathbf{S}(t))=v(r,\mathbf{S}(r))+{\int_{r}^{t}}\boldsymbol{\xi}^{\mathbf{S}}(s)\,\,\mathrm{d} \mathbf{S}(s)\qquad\text{for \(t\in\,[r,u]\).} $$ -
(b)
The function v satisfies the parabolic equation
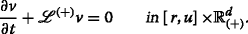 (2.8)
(2.8)
Moreover, if these equivalent conditions hold, then ξ S in (a) must necessarily be of the form
Now suppose that \(f:{\mathbb {R}}^{d}_{(+)}\to {\mathbb {R}}\) is a continuous function for which there exists a solution v to the following terminal-value problem,

For  and t∈ [ 0,T), we can define
and t∈ [ 0,T), we can define
We then obtain from Proposition 2.3 that
Thus, (ξ S,η S) is a self-financing trading strategy with portfolio value V S(t)=v(t,S(t)). Since the function v is continuous on \([0,T]\times {\mathbb {R}}^{d}_{(+)}\), the limit \(V^{\mathbf {S}}(T):={\lim }_{t\uparrow T}V^{\mathbf {S}}(t)\) exists and satisfies

In this sense, (ξ S,η S) is a strictly pathwise hedging strategy for the derivative with payoff f(S(T)).
The preceding argument was first made by Bick and Willinger (1994, Proposition 3) in a one-dimensional setting. It is remarkable in several respects. For instance, consider the one-dimensional case with a(t,x)=σ 2 x 2 for some σ>0 so that (TVP+) becomes the standard Black–Scholes equation, which can be solved for a large class of payoff functions f. The preceding argument then shows that the Black–Scholes formula—which is nothing other than an explicit formula for v(0,S 0)—can be derived without any probabilistic assumptions whatsoever. It follows, in particular, that the fundamental assumption underlying the Black–Scholes formula is not the log-normal distribution of asset price returns, but the fact that the quadratic variation of the asset prices is of the form \({\langle S,S \rangle }(t) = \sigma ^{2}{\int _{0}^{t}}S(s)^{2}{\,\mathrm {d}} s\). Let us now state general existence results for solutions of (TVP) and (TVP+), which in the case of (TVP) is taken from Janson and Tysk (2004). Recall that we assume that a(t,x) is positive definite for all t and x.
Theorem 2.4.
Suppose that \(f\in C \left ({\mathbb {R}}^{d}_{(+)}\right)\) has at most polynomial growth in the sense that |f(x)|≤c 0(1+|x|p) for some constants c 0,p>0. Then, under the following conditions, (TVP (+)) admits a unique solution v(t,x) within the class of functions that are of at most polynomial growth uniformly in t.
-
(a)
(Janson and Tysk, 2004 , Theorem A.14) In case of (TVP), we suppose that a ij (t,x) is locally Hölder continuous on \([\!0,T)\times {\mathbb {R}}^{d}\) and that |a ij (t,x)|≤c 1(1+|x|2) for a constant c 1≥0, all \((t,\mathbf {x})\in \,[\!0,T]\times {\mathbb {R}}^{d}\), and all i,j.
-
(b)
In case of (TVP +), we suppose that a ij (t,x) is bounded and locally Hölder continuous on \([\!0,T)\times {\mathbb {R}}^{d}\) for all i,j.
Our next goal is to extend the preceding hedging argument to the case of a path-dependent exotic option. In practice, the payoff of such a derivative is usually of the form
where 0=t 0<t 1<⋯<t N =T denote the fixing times of daily closing prices and h is a certain function.
Theorem 2.5.
Suppose that the conditions of Theorem 2.4 are satisfied and h in (2.12) is a locally Lipschitz continuous function on \(({\mathbb {R}}_{(+)}^{d})^{N+1}\) with a Lipschitz constant that grows at most polynomially. That is, there exist p≥0 and L≥0 such that, for |x i |,|y i |≤m,
Then, letting
the following recursive scheme for functions \(v_{k}:\left [t_{k},t_{k+1}\right ] \times \left ({\mathbb {R}}^{d}_{(+)}\right)^{k+1}\times {\mathbb {R}}^{d}_{(+)}\to {\mathbb {R}}\), for k=0,…,N−1, is well-defined.
-
For k=N−1,N−2,…,0, the function f k+1(x):=v k+1(t k+1,x 0,…,x k ,x,x) is continuous in x, and (t,x)↦v k (t,x 0,…,x k ,x) is the solution of (T V P (+)) with terminal condition f k+1 at time t k+1.
The condition on the local Lipschitz continuity of h in the preceding result can often be relaxed in more specific situations. Examples are the pathwise versions of the (d-dimensional) Bachelier and Black–Scholes models, which both correspond to the choice \(a_{ij}(t,\mathbf {x})=\widetilde {a}_{ij}\) for a constant positive definite matrix \((\widetilde {a}_{ij})\). In these cases the recursive scheme in Theorem 2.5 can be solved for large classes of payoff functions h without requiring local Lipschitz continuity. As a matter of fact, even the continuity of h can be relaxed so as to account for discontinuous payoffs as, e.g., in barrier options. This also applies to the strictly pathwise hedging argument that we are going to formulate next. However, these relaxations need case-by-case arguments. We therefore do not spell them out explicitly here and leave the details to the interested reader.
Now let H be an exotic option as in (2.12) and suppose that the recursive scheme in Theorem 2.5 holds for functions v k , k=0,…,N. When denoting by ∇ x v k the gradient of the function x↦v k (t,x 0,…,x k ,x), then
is a self-financing trading strategy on each interval [ t k ,t k+1) in the sense that
The continuity of t↦v k (t,S(t 0),…,S(t k ),S(t)) implies the existence of the limit
and hence allows us to define
where ℓ is the largest k such that t k <t. With these conventions, we obtain the following Delta hedging result.
Corollary 2.6.
Let H be an exotic option as in (2.12) and suppose that the recursive scheme in Theorem 2.5 holds for functions v
k
, k=0,…,N. Then, for each  , the strategy (2.13) is self-financing in the above sense and satisfies
, the strategy (2.13) is self-financing in the above sense and satisfies
In this sense, (ξ S,η S) is a strictly pathwise Delta hedging strategy for H.
The preceding corollary establishes a general, strictly pathwise hedging result for a large class of exotic options arising in practice. It also identifies v
0(0,S(t
0)) as the amount of cash needed at t=0 so as to perfectly replicate the payoff H for all price trajectories in  . In continuous-time finance, this amount is usually equated with an arbitrage-free price for H. In our situation, however, the interpretation of v
0(0,S(t
0)) as an arbitrage-free price lacks an essential ingredient: We do not know whether our class of trading strategies is indeed arbitrage-free with respect to all possible price trajectories in
. In continuous-time finance, this amount is usually equated with an arbitrage-free price for H. In our situation, however, the interpretation of v
0(0,S(t
0)) as an arbitrage-free price lacks an essential ingredient: We do not know whether our class of trading strategies is indeed arbitrage-free with respect to all possible price trajectories in  . This question will now be explored in the subsequent section. Our corresponding result, Theorem 3.3, gives sufficient conditions under which trading strategies, as those in Corollary 2.6, do indeed not generate arbitrage in our pathwise framework. Theorem 3.3 will be the main result of this paper.
. This question will now be explored in the subsequent section. Our corresponding result, Theorem 3.3, gives sufficient conditions under which trading strategies, as those in Corollary 2.6, do indeed not generate arbitrage in our pathwise framework. Theorem 3.3 will be the main result of this paper.
Remark 2.7. (Robustness of the hedging strategy)
The strategy (2.13) yields a perfect hedge for the exotic option H only if the actually realized price trajectory, S, belongs to the set  . In reality, however, the realized quadratic variation is typically subject to uncertainty, and therefore it may turn out a posteriori that S does actually not belong to
. In reality, however, the realized quadratic variation is typically subject to uncertainty, and therefore it may turn out a posteriori that S does actually not belong to  . If S nevertheless belongs to Q
V
d, one can then speak of volatility uncertainty. One possible approach to volatility uncertainty was developed in (Lyons 1995), where, for the case in which H=h(S(T)), the linear Eq. (TVP+) is replaced by a certain nonlinear partial differential equation that corresponds to a worst-case approach within a class of price trajectories whose realized volatility may vary within a given set. A different approach to volatility uncertainty was proposed in (El Karoui et al. 1998) for the case d=1, in which we write S instead of the vector notation S. Although (El Karoui et al. 1998) is set up in a diffusion framework, it is straightforward to translate the comparison result of (El Karoui et al. 1998, Theorem 6.2) into a strictly pathwise framework. For options of the form H=h(S(T)) with h≥0 convex, one then gets that the Delta hedge (2.13) is robust in the sense that it is still a superhedge as long as a overestimates the realized quadratic variation, i.e., \({\int _{r}^{t}}a(s,S(s)){\,\mathrm {d}} s\ge {\langle }S,S{\rangle }(t)-{\langle }S,S{\rangle }(r)\) for 0≤r≤t≤T. Thus, if a Delta hedging strategy is robust, then a trader can monitor its performance by comparing a(t,S(t)) to the realized quadratic variation 〈S,S〉. In (Schied and Stadje 2007), it was analyzed to what extent the preceding result can be extended to exotic payoffs of the form H=h(S(t
0),…,S(t
N
)). It was shown that robustness then breaks down for a large class of relevant convex payoff functions h, but that it still holds if h is directionally convex.
. If S nevertheless belongs to Q
V
d, one can then speak of volatility uncertainty. One possible approach to volatility uncertainty was developed in (Lyons 1995), where, for the case in which H=h(S(T)), the linear Eq. (TVP+) is replaced by a certain nonlinear partial differential equation that corresponds to a worst-case approach within a class of price trajectories whose realized volatility may vary within a given set. A different approach to volatility uncertainty was proposed in (El Karoui et al. 1998) for the case d=1, in which we write S instead of the vector notation S. Although (El Karoui et al. 1998) is set up in a diffusion framework, it is straightforward to translate the comparison result of (El Karoui et al. 1998, Theorem 6.2) into a strictly pathwise framework. For options of the form H=h(S(T)) with h≥0 convex, one then gets that the Delta hedge (2.13) is robust in the sense that it is still a superhedge as long as a overestimates the realized quadratic variation, i.e., \({\int _{r}^{t}}a(s,S(s)){\,\mathrm {d}} s\ge {\langle }S,S{\rangle }(t)-{\langle }S,S{\rangle }(r)\) for 0≤r≤t≤T. Thus, if a Delta hedging strategy is robust, then a trader can monitor its performance by comparing a(t,S(t)) to the realized quadratic variation 〈S,S〉. In (Schied and Stadje 2007), it was analyzed to what extent the preceding result can be extended to exotic payoffs of the form H=h(S(t
0),…,S(t
N
)). It was shown that robustness then breaks down for a large class of relevant convex payoff functions h, but that it still holds if h is directionally convex.
Absence of pathwise arbitrage
We are now going to study the absence of pathwise arbitrage within a class of strategies that is suggested by the pathwise Delta hedging strategies constructed in Theorem 2.5 and Corollary 2.6. We refer to the paragraph preceding Remark 2.7 for a motivation of this problem. Let us first introduce the class of strategies we will consider.
Definition 3.1.
Suppose that \(N\in \mathbb {N}\), 0=t
0<t
1<⋯<t
N
=t
N+1=T, and v
k
(k=0,…,N) are real-valued continuous functions on \([\!t_{k},t_{k+1}]\times \left ({\mathbb {R}}^{d}_{(+)}\right)^{k+1}\times {\mathbb {R}}^{d}_{(+)}\) such that, for k=0,…,N−1, the function (t,x)↦v
k
(t,x
0,…,x
k
,x) is the solution of (TVP(+)) with terminal condition f
k+1(x):=v
k+1(t
k+1,x
0,…,x
k
,x,x) at time t
k+1. For  we then define ξ
S as in (2.13) and
we then define ξ
S as in (2.13) and
where the pathwise Itô integral is understood as in (2.14). By  we denote the collection of all pairs (v
0(0,·),ξ
·) that arise in this way.
we denote the collection of all pairs (v
0(0,·),ξ
·) that arise in this way.
Theorem 2.5 gives sufficient conditions for the existence of a family of functions (v k ) as in the preceding definition, but these conditions are not necessary. In particular, as mentioned above, the local Lipschitz continuity of the terminal function v N can be relaxed in many situations. We can now define our strictly pathwise notion of an arbitrage strategy.
Definition 3.2.
((Admissible) arbitrage opportunity) A pair  is called an arbitrage opportunity for
is called an arbitrage opportunity for  if the following conditions hold.
if the following conditions hold.
-
(a)
\(V^{\mathbf {S}}_{\boldsymbol {\xi }}(T)\ge 0\) for all
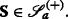 .
. -
(b)
There exists at least one
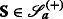 for which \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(0)=v_{0}(0,\mathbf {S}(0))\le 0\) and \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(T_{0})>0\) for some T
0∈(0,T].
for which \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(0)=v_{0}(0,\mathbf {S}(0))\le 0\) and \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(T_{0})>0\) for some T
0∈(0,T].
An arbitrage opportunity (v 0(0,·),ξ ·) will be called admissible if the following condition is also satisfied.
-
(c)
There exists a constant c≥0 such that \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(t)\ge -c\) for all
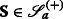 and t∈ [ 0,T].
and t∈ [ 0,T].
Let us comment on the preceding definition. Condition (a) states that one can follow the strategy (v
0(0,·),ξ
·) up to time T without running the risk of ending up with negative wealth at the terminal time. Now let S be as in condition (b). The initial spot value, S
0:=S(0), will then be such that v
0(0,S
0)=V
ξ
S(0)≤0. Hence, for any price trajectory  with \(\widetilde {\mathbf {S}}(0)=\mathbf {S}_{0}\), only a nonpositive initial investment \(v_{0}(0,\mathbf {S}_{0})=V^{\widetilde {\mathbf {S}},\boldsymbol {\xi }}(0)\) is required so as to end up with the nonnegative terminal wealth \(V^{\widetilde {\mathbf {S}},\boldsymbol {\xi }}(T)\ge 0\). Moreover, for the particular price trajectory S, there exists a time T
0 at which one can make the strictly positive profit \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(T_{0})>0\). This profit can be locked in, e.g., by halting all trading from time T
0 onward. In this sense, the strategy (v
0(0,·),ξ
·) is indeed an arbitrage opportunity. Condition (c) is a constraint on the strategy (v
0(0,·),ξ
·) that is analogous to the admissibility constraint that is usually imposed in continuous-time probabilistic models so as to exclude doubling-type strategies. Indeed, it follows, e.g., from Dudley’s (1977) result that standard diffusion models typically admit arbitrage opportunities in the class of strategies whose value process is not bounded from below (see also the discussion in (Jeanblanc et al. 2009, Section 1.6.3)). In our pathwise setting, an example of an arbitrage opportunity that does not satisfy condition (c) will be provided in Example 3.4 below. First, however, let us state the main result of our paper.
with \(\widetilde {\mathbf {S}}(0)=\mathbf {S}_{0}\), only a nonpositive initial investment \(v_{0}(0,\mathbf {S}_{0})=V^{\widetilde {\mathbf {S}},\boldsymbol {\xi }}(0)\) is required so as to end up with the nonnegative terminal wealth \(V^{\widetilde {\mathbf {S}},\boldsymbol {\xi }}(T)\ge 0\). Moreover, for the particular price trajectory S, there exists a time T
0 at which one can make the strictly positive profit \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(T_{0})>0\). This profit can be locked in, e.g., by halting all trading from time T
0 onward. In this sense, the strategy (v
0(0,·),ξ
·) is indeed an arbitrage opportunity. Condition (c) is a constraint on the strategy (v
0(0,·),ξ
·) that is analogous to the admissibility constraint that is usually imposed in continuous-time probabilistic models so as to exclude doubling-type strategies. Indeed, it follows, e.g., from Dudley’s (1977) result that standard diffusion models typically admit arbitrage opportunities in the class of strategies whose value process is not bounded from below (see also the discussion in (Jeanblanc et al. 2009, Section 1.6.3)). In our pathwise setting, an example of an arbitrage opportunity that does not satisfy condition (c) will be provided in Example 3.4 below. First, however, let us state the main result of our paper.
Theorem 3.3. (Absence of admissible arbitrage)
Suppose that a(t,x) is continuous, bounded, and positive definite for all \((t,\mathbf {x})\in \,[\!0,\widetilde {T}]\times {\mathbb {R}}_{(+)}^{d}\), where \(\widetilde {T}>T\). Then there are no admissible arbitrage opportunities in  .
.
Example 3.4.
(A non-admissible arbitrage opportunity) Suppose that d=1 and a≡2. Then the assumptions of Theorem 3.3 are clearly satisfied. Moreover,  and (TVP) is the time-reversed Cauchy problem for the standard heat equation. There are many explicit examples of nonvanishing functions v satisfying (TVP) with terminal condition f≡0; see, e.g., (Widder 1975, Section II.6). By Widder’s uniqueness theorem for nonnegative solutions of the heat equation, (Widder 1975, Theorem VIII.2.2), any such function v must be unbounded from above and from below on every nontrivial strip \([\!t,T]\times {\mathbb {R}}\) with t<T. In particular, there must be 0≤t
0<t
1<T and \(x_{0},x_{1}\in {\mathbb {R}}\) such that v(t
0,x
0)=0 and v(t
1,x
1)>0. By means of a time shift, we can assume without loss of generality that t
0=0. It can be shown easily that
and (TVP) is the time-reversed Cauchy problem for the standard heat equation. There are many explicit examples of nonvanishing functions v satisfying (TVP) with terminal condition f≡0; see, e.g., (Widder 1975, Section II.6). By Widder’s uniqueness theorem for nonnegative solutions of the heat equation, (Widder 1975, Theorem VIII.2.2), any such function v must be unbounded from above and from below on every nontrivial strip \([\!t,T]\times {\mathbb {R}}\) with t<T. In particular, there must be 0≤t
0<t
1<T and \(x_{0},x_{1}\in {\mathbb {R}}\) such that v(t
0,x
0)=0 and v(t
1,x
1)>0. By means of a time shift, we can assume without loss of generality that t
0=0. It can be shown easily that  contains trajectories that can connect the two points x
0 and x
1 within time t
1−t
0, and so it follows that the function v gives rise to an arbitrage opportunity.
contains trajectories that can connect the two points x
0 and x
1 within time t
1−t
0, and so it follows that the function v gives rise to an arbitrage opportunity.
Extension to functionally dependent strategies
Recall from (2.12) our representation H=h(S(t 0),…,S(t N )) of the payoff of an exotic option, based on asset prices sampled at the N+1 dates 0=t 0<t 1<⋯<t N =T. If N is large, it may be convenient to use a continuous-time approximation of the payoff H. For instance, the payoff \(H=\left (\frac {1}{N} \sum _{n=1}^{N}S^{1}_{t_{n}}-K\right)^{+}\) of an average-price Asian call option on the first asset, S 1, can be approximated by a call option based on a continuous-time average of asset prices, \(H\approx \left (\frac {1}{T}{\int _{0}^{T}}{S^{1}_{t}}\,dt-K\right)^{+}\). Approximations of this type may be easier to treat analytically and are standard in the textbook literature. In this section, we extend our preceding results to a situation that covers such continuous-time approximations of (2.12). That is, we will consider payoffs of the form H(S), where S describes the entire path of the underlying price trajectory up to time T, and H is a suitable mapping from the Skorohod space \(D([\!0,T],{\mathbb {R}}^{d})\) to \({\mathbb {R}}.\) This will involve functional Itô calculus as introduced by (Dupire 2009) and further developed by Cont and Fournié (2010). In the sequel, we will use the same notation as in (Cont and Fournié 2010).
For a d-dimensional càdlàg path X in the Skorohod space \(D([\!0,T], \mathbb {R}^{d})\) we write X(t) for the value of X at time t and X t =(X(u))0≤u≤t for the restriction of X to the interval [0,t]. Hence, \(\mathbf {X}_{t}\in D([\!0,t], \mathbb {R}^{d})\). We will work with non-anticipative functionals as defined in (Cont and Fournié 2010, Definition 1), i.e., with a family F=(F t ) t∈[0,T] of maps \( F_{t}:D([0,t], \mathbb {R}^{d})\mapsto \mathbb {R}.\) For all further notation and relevant definitions, we refer to (Cont and Fournié 2010, Section 1).
The functional Itô formula (in the form of (Cont and Fournié 2010, Theorem 3)) yields that we can define general admissible integrands ξ in the following way, so as to ensure that the pathwise Itô integral \({\int _{r}^{t}}\boldsymbol {\xi }(s){\,\mathrm {d}}\mathbf {S}(s)\) exists for all t∈ [ r,u]⊂ [ 0,T] as a finite limit of Riemann sums; see (Cont and Fournié 2010, p. 1051).
Definition 4.1.
(General admissible integrands) Suppose that 0≤r<u≤T, \(m\in \mathbb {N}\), \(\mathbf {V}:[r,u]\to {\mathbb {R}}^{m}\) is càdlàg and satisfies \(\sup _{t\in [r,u]\textbackslash \mathbb {T}_{n}\cap [r,u]}\arrowvert \mathbf {V}(t)-\mathbf {V}(t-) \arrowvert \to 0\), and F is a non-anticipative functional in \( \mathbb {C}^{1,2}([\!r,u])\) (see (Cont and Fournié 2010, Definition 9)) such that the following regularity conditions are satisfied:
-
F depends in a predictable manner on its second argument V, i.e.,
$$ F_{t}(\mathbf{X}_{t}, \mathbf{V}_{t})= F_{t}(\mathbf{X}_{t}, \mathbf{V}_{t-}), $$where V t− denotes the path defined on [r,t] by
$$ \mathbf{V}_{t-}(s)=\mathbf{V}(s),\quad s\in\,[\!r,t),\quad \mathbf{V}_{t-}(t)=\mathbf{V}(t-), $$ -
F, its vertical derivative ∇ x F, and its second vertical derivative \(\nabla ^{2}_{\mathbf {x}}F\) belong to the class \(\mathbb {F}^{\infty }_{l}\) (see (Cont and Fournié 2010, Definition 3)),
-
the horizontal derivative \(\mathcal {D} F\) as well as the second vertical derivative \(\nabla ^{2}_{\mathbf {x}}F\) of F satisfy the local boundedness condition (Cont and Fournié 2010, equation (9)).
Then
is called a general admissible integrand for S∈Q V d. Here, S [r,u] denotes the restriction of S to the interval [ r,u].
In analogy to Proposition 2.3, we will now characterize self-financing trading strategies that may depend on the entire past evolution of the particular realization  . For an interval I⊂ [ 0,T] with nonempty interior,
. For an interval I⊂ [ 0,T] with nonempty interior,  , we denote by \({\mathbb {C}}^{1,2}(I)\) the class of all non-anticipative functionals on \(\bigcup _{t\in [a,b]} D([a,t], {\mathbb {R}}^{d}_{(+)})\) that are horizontally differentiable and twice vertically differentiable on
, we denote by \({\mathbb {C}}^{1,2}(I)\) the class of all non-anticipative functionals on \(\bigcup _{t\in [a,b]} D([a,t], {\mathbb {R}}^{d}_{(+)})\) that are horizontally differentiable and twice vertically differentiable on  and whose derivatives are continuous at fixed times and admit continuous extensions to I.
and whose derivatives are continuous at fixed times and admit continuous extensions to I.
Thus, lifting the second-order differential operators  and
and  yields the following operators on path space,
yields the following operators on path space,

The following proposition is a functional version of Proposition 2.3.
Proposition 4.2.
Suppose that 0≤r<u≤T and let \(F\in \mathbb {C}^{1,2}([r,u])\) be a non-anticipative functional satisfying the conditions from Definition 4.1.
Then the following conditions are equivalent.
-
(a)
For each
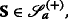 , there exists a general admissible integrand ξ
S on [r,u] such that
$$F_{t}\left(\mathbf{S}_{[r,u],t}\right) = F_{r}\left(\mathbf{S}_{[r,u],r}\right) + {\int_{r}^{t}}\boldsymbol{\xi}^{\mathbf{S}}(s)\,\,\mathrm{d} \mathbf{S}(s)\qquad\text{for \(t\in\,[r,u]\).} $$
, there exists a general admissible integrand ξ
S on [r,u] such that
$$F_{t}\left(\mathbf{S}_{[r,u],t}\right) = F_{r}\left(\mathbf{S}_{[r,u],r}\right) + {\int_{r}^{t}}\boldsymbol{\xi}^{\mathbf{S}}(s)\,\,\mathrm{d} \mathbf{S}(s)\qquad\text{for \(t\in\,[r,u]\).} $$ -
(b)
The functional F satisfies the path-dependent parabolic equation
 (4.1)
(4.1)
Moreover, if these equivalent conditions hold, then ξ S in (a) must necessarily be of the form
Now suppose that for suitably given \(H:D([\!0,T],\mathbb {R}^{d}_{(+)})\to \mathbb {R}\) there exists a solution F to the following path-dependent terminal-value problem,

Note that the terminal condition H has to be defined on the Skorohod space \(D([0,T],{\mathbb {R}}^{d}_{(+)})\) as opposed to \(C([0,T],{\mathbb {R}}^{d}_{(+)})\), because we need to take its vertical derivatives, which requires applying discontinuous shocks.
Then, for  and t∈ [ 0,T), we can define
and t∈ [ 0,T), we can define
Proposition 4.2 gives
whence we infer that (ξ S,η S) is a self-financing trading strategy with portfolio value V S(t)=F t (S t ). Since the functional F is left-continuous on [ 0,T] and S is continuous, the limit \(V^{\mathbf {S}}(T):={\lim }_{t\uparrow T}V^{\mathbf {S}}(t)\) exists and satisfies

Thus, (ξ S,η S) is a strictly pathwise hedging strategy for the derivative with payoff H=H(S).
In the next step, we will explore conditions yielding the existence and uniqueness of solutions to (FTVP) and (FTVP+). Path-dependent PDEs such as (4.1) are closely related to backward stochastic differential equations (BSDEs) generalizing the (functional) Feynman-Kac formula (Dupire 2009). In (Peng and Wang 2016), a one-to-one correspondence between a functional BSDE and a path-dependent PDE is established for the Brownian case. This was then generalized in (Ji and Yang 2013) to the case of solutions to stochastic differential equations with functionally dependent drift and diffusion coefficients.
We will now use (Ji and Yang 2013, Theorem 20) to formulate conditions such that (FTVP) and (FTVP+) admit unique solutions. To this end, we will need the following regularity conditions from (Peng and Wang 2016, Definition 3.1).
Definition 4.3.
The functional \(H:D([0,T],{\mathbb {R}}^{d}) \mapsto \mathbb {R}\) on the Skorohod space \(D([\!0,T],{\mathbb {R}}^{d})\) is of class \(C^{2}(D([\!0,T],{\mathbb {R}}^{d}))\) if for all \(\mathbf {X}\in D([0,T],{\mathbb {R}}^{d})\) and t∈[0,T], there exist \(\mathbf {p}_{1}\in {\mathbb {R}}^{d}\) and \(\mathbf {p}_{2}\in {\mathbb {R}}^{d}\times {\mathbb {R}}^{d}\) so that p 2 is symmetric and the following holds
where \(\mathbf {X}_{{\mathbf {X}_{t}^{h}}}(u):=\mathbf {X}(u)I_{[0,t)}(u) + (\mathbf {X}(u) + \mathbf {h})I_{[t,T]}(u). \) We denote \(H^{\prime }_{\mathbf {X}_{t}}(\mathbf {X}):=\mathbf {p}_{1}\) and H X t ″(X):=p 2. Moreover, \(H:D\left ([\!0,T],{\mathbb {R}}^{d}\right) \mapsto \mathbb {R}\) is of class \(C_{l,lip}^{2}\left (D \left ([\!0,T],{\mathbb {R}}^{d}\right) \right)\) if \(H^{\prime }_{\mathbf {X}_{t}}(\mathbf {X})\) and H X t ″(X) exist for all \(\mathbf {X}\in D\left ([\!0,T],{\mathbb {R}}_{(+)}^{d}\right)\) and t∈ [ 0,T], and if there are constants C,k>0 such that for all \(\mathbf {X},\mathbf {Y}\in D\left ([\!0,T],{\mathbb {R}}_{(+)}^{d}\right)\) (with ∥·∥ denoting the supremum norm),
Theorem 4.4.
Suppose that the terminal condition H of (FTVP (+)) is of class \(C^{2}_{l,lip}\left (D \left ([\!0,T],{\mathbb {R}}_{(+)}^{d} \right)\right)\). Then, under the following conditions, (FTVP (+)) admits a unique solution \(F\in {\mathbb {C}}^{1,2}([0,T))\).
-
(a)
(Ji and Yang, 2013 , Theorem 20) In case of (FTVP), we suppose that a(t,X(t))=σ(t,X(t))σ(t,X(t))⊤ with a Lipschitz continuous volatility matrix σ.
-
(b)
In case of (FTVP +), we suppose that a(t,X(t))=σ(t,X(t))σ(t,X(t))⊤ with a Lipschitz continuous volatility matrix σ such that a ii (t,X(t)) is also Lipschitz continuous.
Remark 4.5.
Note that analogous conditions on the covariance, respectively, volatility structure, can also be formulated for the case where these quantities are path-dependent, thanks to (Ji and Yang 2013, Theorem 20). However, for the purpose of this paper, which is establishing conditions on the covariance of the underlying under which no admissible arbitrage opportunities exist, we must stick to the choice of Markovian volatility in order to be able to apply a support theorem later on.
As above, the quantity F 0(S 0) can be identified as the amount of cash needed at t=0 so as to perfectly replicate the payoff H. But in order to interpret F 0(S 0) as an arbitrage-free price, we have to know whether our class of trading strategies is indeed arbitrage-free. Below we will formulate Theorem 4.7, which is a functional analogue of Theorem 3.3.
Definition 4.6.
Suppose that the non-anticipative functional F satisfying the conditions from Definition 4.1 is the solution of the path-dependent heat Eq. (4.1)

For  , we then define ξ
S as in (4.2) (on [ 0,T)) and
, we then define ξ
S as in (4.2) (on [ 0,T)) and
By  we denote the collection of all pairs (F
0(·),ξ
·) that arise in this way.
we denote the collection of all pairs (F
0(·),ξ
·) that arise in this way.
The notion of an (admissible) arbitrage opportunity for  in the functional setting is defined in analogy to Definition 3.2; we only have to replace
in the functional setting is defined in analogy to Definition 3.2; we only have to replace  by
by  .
.
Theorem 4.7. (Absence of admissible arbitrage)
Suppose that a(t,X(t)) is continuous, bounded, and positive definite for all \((t,\mathbf {X}(t))\in \,[\!0,\widetilde {T}]\times {\mathbb {R}}_{(+)}^{d}\), where \(\widetilde {T}>T\). Then there are no admissible arbitrage opportunities in  .
.
Proofs
Proofs of the results from Sections “Strictly pathwise hedging of exotic derivatives and Absence of pathwise arbitrage”
Proof of Proposition 2.1.
We first consider the case i=j. Then,
Summing over \(s\in \mathbb {T}_{n}\) yields
where \(t_{n}=\max \{s'\,|\,s\in \mathbb {T}_{n},\, s\le t\}\searrow t\) as n ↑ ∞. Clearly, the limit of the left-hand side exists if and only if the limit of the right-hand side exists, which implies the result for i=j. In case i≠j, the result follows just as above by using the already established existence of 〈S k ,S k 〉(t) for all k and t and by noting that \(\sum _{k,\ell \in \{i,j\}}{\langle }S_{k},S_{\ell }{\rangle }={\left \langle S_{i}+S_{j},S_{i}+S_{j} \right \rangle }\). □
Proof of Proposition 2.3.
The pathwise Itô formula yields that for  ,
,

This immediately yields that (b) implies (a) and that (2.9) must hold.
Let us now assume that (a) holds. Then

Since the right-hand side has zero quadratic variation (Sondermann 2006, Proposition 2.2.2), the same must be true of the left-hand side. By (Schied 2014, Proposition 12), the quadratic variation of the left-hand side is given by
in case of  . Taking the derivative with respect to t gives
. Taking the derivative with respect to t gives
for all t, and the fact that the matrix a(t,S(t)) is positive definite yields that (2.9) must hold. For  , the matrix a(s,S(s)) needs to be replaced by the matrix with components a
ij
(s,S(s))S
i
(s)S
j
(s), and we arrive at (2.9) by the same arguments as in the case of
, the matrix a(s,S(s)) needs to be replaced by the matrix with components a
ij
(s,S(s))S
i
(s)S
j
(s), and we arrive at (2.9) by the same arguments as in the case of  . Plugging (2.9) into (5.2) and using (a) implies that the rightmost integral in (5.2) vanishes identically, which establishes (b) by again taking the derivative with respect to t. □
. Plugging (2.9) into (5.2) and using (a) implies that the rightmost integral in (5.2) vanishes identically, which establishes (b) by again taking the derivative with respect to t. □
Now we prepare for the proof of Theorem 2.4 (b). The following lemma can be proved by means of a straightforward computation.
Lemma 5.1.
For \(\mathbf {x} = \left (x_{1},\dots, x_{d}\right)^{\top }\in {\mathbb {R}}^{d}\) let \(\exp (\mathbf {x}):=\left (e^{x_{1}},\dots, e^{x_{d}}\right)^{\top }\in {\mathbb {R}}^{d}_{+}\). Then v(t,x) solves (TVP+) if and only if \(\widetilde {v}(t,\mathbf {x}):=v(t,\exp (\mathbf {x}))\) solves

where \(\widetilde {f}(\mathbf {x})=f(\exp (\mathbf {x}))\) and

for \(\widetilde {a}_{ij}(t,\mathbf {x}):=a_{ij}(t,\exp (\mathbf {x}))\) and \(\widetilde {b}_{i}(t,\mathbf {x}):=-\frac {1}{2}a_{ii}(t,\exp (\mathbf {x}))\).
Next, the terminal-value problem \({(\widetilde {\text {TVP}})}\) will be once again transformed into another auxiliary terminal-value problem. To this end, we need another transformation lemma, whose proof is also left to the reader.
Lemma 5.2.
For p>0 let \(g(\mathbf {x}):=1+\sum _{i=1}^{d}e^{p x_{i}}\). Then \(\widetilde {v}(t,\mathbf {x})\) solves \((\widetilde {\text {TVP}})\) if and only if \(\widehat v(t,\mathbf {x}):=g(\mathbf {x})^{-1}\widetilde {v}(t,\mathbf {x})\) solves

where \(\widehat f(\mathbf {x})=\widetilde {f}(\mathbf {x})/g(\mathbf {x})\) and

for
Proof of Theorem 2.4.
We will show that \({(\widetilde {\text {TVP}})}\) admits a solution \(\widetilde {v}\) if \(|\widetilde {f}(\mathbf {x})|\le c(1+\sum _{i=1}^{d}e^{p x_{i}})\) for some p>0 and that \(\widetilde {v}\) is unique in the class of functions that satisfy a similar estimate uniformly in t. To this end, note that the coefficients of  satisfy the conditions of (Janson and Tysk 2004, Theorem A.14), i.e., \(\widehat a(t,\mathbf {x})=\widetilde {a}(t,\mathbf {x})\) is positive definite, there are constants c
1, c
2, c
3 such that for all t, x, and i,j we have that \(|\widetilde {a}_{ij}(t,\mathbf {x})|\le c_{1}(1+|\mathbf {x}|^{2})\), \(|\widehat b_{i}(t,\mathbf {x})|\le c_{2}(1+|\mathbf {x}|)\), \(|\widehat c(t,\mathbf {x})|\le c_{3}\), and \(\widetilde {a}_{ij}\), \(\widehat b_{i}\), and \(\widehat c\) are locally Hölder continuous in \([0,T)\times {\mathbb {R}}^{d}\). It therefore follows that \({(\widehat {\text {TVP}})}\) admits a unique bounded solution \(\widehat v\) whenever \(\widehat f\) is bounded and continuous. But then \(\widetilde {v}(t,\mathbf {x}):=g(\mathbf {x})\widehat v(t,\mathbf {x})\) solves \({(\widetilde {\text {TVP}})}\) with terminal condition \(\widetilde {f}(\mathbf {x}):=g(\mathbf {x})\widehat f(\mathbf {x})\). Hence, \({(\widetilde {\text {TVP}})}\) admits a solution whenever \(|\widetilde {f}(\mathbf {x})|\le c\left (1+\sum _{i=1}^{d}e^{p x_{i}}\right)\) for some p>0. Lemma 5.1 now establishes the existence of solutions to (TVP+) if the terminal condition is continuous and has at most polynomial growth. □
satisfy the conditions of (Janson and Tysk 2004, Theorem A.14), i.e., \(\widehat a(t,\mathbf {x})=\widetilde {a}(t,\mathbf {x})\) is positive definite, there are constants c
1, c
2, c
3 such that for all t, x, and i,j we have that \(|\widetilde {a}_{ij}(t,\mathbf {x})|\le c_{1}(1+|\mathbf {x}|^{2})\), \(|\widehat b_{i}(t,\mathbf {x})|\le c_{2}(1+|\mathbf {x}|)\), \(|\widehat c(t,\mathbf {x})|\le c_{3}\), and \(\widetilde {a}_{ij}\), \(\widehat b_{i}\), and \(\widehat c\) are locally Hölder continuous in \([0,T)\times {\mathbb {R}}^{d}\). It therefore follows that \({(\widehat {\text {TVP}})}\) admits a unique bounded solution \(\widehat v\) whenever \(\widehat f\) is bounded and continuous. But then \(\widetilde {v}(t,\mathbf {x}):=g(\mathbf {x})\widehat v(t,\mathbf {x})\) solves \({(\widetilde {\text {TVP}})}\) with terminal condition \(\widetilde {f}(\mathbf {x}):=g(\mathbf {x})\widehat f(\mathbf {x})\). Hence, \({(\widetilde {\text {TVP}})}\) admits a solution whenever \(|\widetilde {f}(\mathbf {x})|\le c\left (1+\sum _{i=1}^{d}e^{p x_{i}}\right)\) for some p>0. Lemma 5.1 now establishes the existence of solutions to (TVP+) if the terminal condition is continuous and has at most polynomial growth. □
Remark 5.3.
It follows from the preceding argument that, if |f(x)|≤c(1+|x|p), then the corresponding solution v of (TVP+) satisfies \(|v(t,\mathbf {x})|\le \widetilde {c}(1+|\mathbf {x}|^{p})\) for a certain constant \(\widetilde {c}\) and with the same exponent p.
Proof of Theorem 2.5.
We first prove the result in the case of (TVP). The function v k will be well-defined if f k+1 is continuous and has at most polynomial growth. It is easy to see that these two properties will follow if v k+1 satisfies the following three conditions:
-
(i)
(x 0,…,x k+1,x)↦v k+1(t,x 0,…,x k+1,x) has at most polynomial growth;
-
(ii)
x↦v k+1(t k+1,x 0,…,x k+1,x) is continuous for all x 0,…,x k+1;
-
(iii)
(x 0,…,x k+1)↦v k+1(t,x 0,…,x k+1,x) is locally Lipschitz continuous, uniformly in t and locally uniformly in x, with a Lipschitz constant that grows at most polynomially. More precisely, there exist p≥0 and L≥0 such that, for |x|,|x i |,|y i |≤m and t∈ [ t k+1,t k+2],
$$\left| v_{k+1}(t,\mathbf{x}_{0},\dots, \mathbf{x}_{k+1},\mathbf{x})-v_{k+1}(t,\mathbf{y}_{0},\dots, \mathbf{y}_{k+1},\mathbf{x})\right|\le (1+m^{p})L\sum\limits_{i=0}^{k+1}|\mathbf{x}_{i}-\mathbf{y}_{i}|. $$
We will now show that v k inherits properties (i), (ii), and (iii) from v k+1. Since these properties are obviously satisfied by v N , the assertion will then follow by backward induction.
To establish (i), let p,c>0 be such that \(\widetilde {f}_{k+1}(\mathbf {x}):=c\left (|\mathbf {x}_{0}|^{p}+\cdots +|\mathbf {x}_{k}|^{p}+|\mathbf {x}|^{p}+|\mathbf {x}|^{p}\right)\) satisfies \(-\widetilde {f}_{k+1}\le f_{k+1}\le \widetilde {f}_{k+1}\). Then let \(\widetilde {v}_{k}(t,\mathbf {x}_{0},\dots, \mathbf {x}_{k},\mathbf {x})\) be the solution of (TVP) with terminal condition \(\widetilde {f}_{k+1}\) at time t k+1. Theorem 2.4, (Janson and Tysk 2004, Theorem A.7), and the linearity of solutions imply that \((\mathbf {x}_{0},\dots, \mathbf {x}_{k},\mathbf {x})\mapsto \widetilde {v}_{k}(t,\mathbf {x}_{0},\dots, \mathbf {x}_{k},\mathbf {x})\) has at most polynomial growth, while the maximum principle in the form of (Janson and Tysk 2004, Theorem A.5) implies that \(-\widetilde {v}_{k}\le v_{k}\le \widetilde {v}_{k}\). This establishes (i).
Condition (ii) is satisfied automatically, as solutions to (TVP) are continuous by construction.
To obtain (iii), let p and L be as in (iii) and x i ,y i be given. We take m so that m≥|x i |∨|y i | for i=1,…,k and let \(\delta :=L\sum _{i=0}^{k}|\mathbf {x}_{i}-\mathbf {y}_{i}|\). Then
Now we define u(t,x) as the solution of (TVP) with terminal condition u(t k+1,x)=|x|p at time t k+1. Theorem 2.4 implies that u is well defined, and the maximum principle and (Janson and Tysk 2004, Theorem A.7) imply that 0≤u(t,x)≤c|x|p for some constant c≥0. Another application of the maximum principle yields that
for all t and x, which establishes that (iii) holds for v k with the same p and the new Lipschitz constant (1+c)L.
Now we turn to the proof in case of (TVP+). It is clear from our proof of Theorem 2.4 (b) that (TVP+) inherits the maximum principle from \((\widehat {\text {TVP}})\). Moreover, Remark 5.3 shows that v k inherits property (i) from v k+1. So Remark 5.3 can replace (Janson and Tysk 2004, Theorem A.7) in the preceding argument. Therefore, the proof for (TVP+) can be carried out in the same way as for (TVP). □
Proof of Theorem 3.3.
We first prove the result in case of  . Let us suppose by way of contradiction that there exists an admissible arbitrage opportunity in
. Let us suppose by way of contradiction that there exists an admissible arbitrage opportunity in  , and let 0=t
0<t
1<⋯<t
N
=t
N+1=T and v
k
denote the corresponding time points and functions as in Definition 3.1.
, and let 0=t
0<t
1<⋯<t
N
=t
N+1=T and v
k
denote the corresponding time points and functions as in Definition 3.1.
Under our assumptions, the martingale problem for the operator  is well-posed (Stroock and Varadhan 1969). Let \({\mathbb {P}}_{t,\mathbf {x}}\) denote the corresponding Borel probability measures on \(C([\!t,T],{\mathbb {R}}^{d})\) under which the coordinate process, (X(u))
t≤u≤T
, is a diffusion process with generator
is well-posed (Stroock and Varadhan 1969). Let \({\mathbb {P}}_{t,\mathbf {x}}\) denote the corresponding Borel probability measures on \(C([\!t,T],{\mathbb {R}}^{d})\) under which the coordinate process, (X(u))
t≤u≤T
, is a diffusion process with generator  and satisfies X(t)=x
\({\mathbb {P}}_{t,\mathbf {x}}\)-a.s. In particular, X
i
is a continuous local \({\mathbb {P}}_{t,\mathbf {x}}\)-martingale for i=1,…,d. Moreover, the support theorem (Stroock and Varadhan 1972, Theorem 3.1) states that the law of (X(u))
t≤u≤T
under \({\mathbb {P}}_{t,\mathbf {x}}\) has full support on \(C_{\mathbf {x}}([\!t,T],{\mathbb {R}}^{d}):=\{\boldsymbol {\omega } \in C([\!t,T],{\mathbb {R}}^{d})\,|\,\boldsymbol {\omega }(t)=\mathbf {x}\}\).
and satisfies X(t)=x
\({\mathbb {P}}_{t,\mathbf {x}}\)-a.s. In particular, X
i
is a continuous local \({\mathbb {P}}_{t,\mathbf {x}}\)-martingale for i=1,…,d. Moreover, the support theorem (Stroock and Varadhan 1972, Theorem 3.1) states that the law of (X(u))
t≤u≤T
under \({\mathbb {P}}_{t,\mathbf {x}}\) has full support on \(C_{\mathbf {x}}([\!t,T],{\mathbb {R}}^{d}):=\{\boldsymbol {\omega } \in C([\!t,T],{\mathbb {R}}^{d})\,|\,\boldsymbol {\omega }(t)=\mathbf {x}\}\).
In a first step, we now use these facts to show that all functions v
k
are nonnegative. To this end, we note first that the support theorem implies that the law of (X(t
1),…,X(t
N
)) under \({\mathbb {P}}_{0,\mathbf {x}}\) has full support on \(({\mathbb {R}}^{d})^{N}\). Since \({\mathbb {P}}_{0,\mathbf {x}}\)-a.e. trajectory in \(C_{\mathbf {x}}([\!0,T],{\mathbb {R}}^{d})\) belongs to  , it follows that the set
, it follows that the set  is dense in \(({\mathbb {R}}^{d})^{N}\). Condition (a) of Definition 3.2 and the continuity of v
N
thus imply that v
N
(T,x
0,…,x
N+1)≥0 for all x
0,…,x
N+1. In the same way, we get from the admissibility of the arbitrage opportunity that v
k
(t,x
0,…,x
k
,x)≥−c for all k, t∈ [ t
k
,t
k+1] and \(\mathbf {x}_{0},\dots,\mathbf {x}_{k},\mathbf {x}\in {\mathbb {R}}^{d}\).
is dense in \(({\mathbb {R}}^{d})^{N}\). Condition (a) of Definition 3.2 and the continuity of v
N
thus imply that v
N
(T,x
0,…,x
N+1)≥0 for all x
0,…,x
N+1. In the same way, we get from the admissibility of the arbitrage opportunity that v
k
(t,x
0,…,x
k
,x)≥−c for all k, t∈ [ t
k
,t
k+1] and \(\mathbf {x}_{0},\dots,\mathbf {x}_{k},\mathbf {x}\in {\mathbb {R}}^{d}\).
For the moment, we fix x 0,…,x N−1 and consider the function u(t,x):=v N−1(t,x 0,…,x N−1,x). Let \(Q\subset {\mathbb {R}}^{d}\) be a bounded domain whose closure is contained in \({\mathbb {R}}^{d}\) and let τ:= inf{s | X(s)∉Q} be the first exit time from Q. By Itô’s formula and the fact that u solves (TVP) we have \({\mathbb {P}}_{t,\mathbf {x}}\)-a.s. for t∈[t N−1,T) that
Since ∇
x
u and the coefficients of  are bounded in the closure of Q, the stochastic integral on the right-hand side is a true martingale. Therefore,
are bounded in the closure of Q, the stochastic integral on the right-hand side is a true martingale. Therefore,
Now let us take an increasing sequence Q 1⊂Q 2⊂⋯ of bounded domains exhausting \({\mathbb {R}}^{d}\) and whose closures are contained in \({\mathbb {R}}^{d}\). By τ n we denote the exit time from Q n . Then, an application of (5.6) for each τ n , Fatou’s lemma in conjunction with the fact that u≥−c, and the already established nonnegativity of u(T,·) yield
This establishes the nonnegativity of v N−1 and in particular of the terminal condition f N−1 for v N−2. We may therefore repeat the preceding argument for v N−2 and so forth. Hence, v k ≥0 for all k.
Now let  and T
0 be such that \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(0)\le 0\) and \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(T_{0})>0\), which exists according to the assumption made at the beginning of this proof. If k is such that t
k
<T
0≤t
k+1 and x
0:=S(0), then v
0(0,x
0)=0 and v
k
(T
0,S(t
0),…,S(t
k
),S(T
0))>0. By continuity, we actually have v
k
(T
0,·)>0 in an open neighborhood \(U\subset C_{\mathbf {x}}([0,T],{\mathbb {R}}^{d})\) of the path S.
and T
0 be such that \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(0)\le 0\) and \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(T_{0})>0\), which exists according to the assumption made at the beginning of this proof. If k is such that t
k
<T
0≤t
k+1 and x
0:=S(0), then v
0(0,x
0)=0 and v
k
(T
0,S(t
0),…,S(t
k
),S(T
0))>0. By continuity, we actually have v
k
(T
0,·)>0 in an open neighborhood \(U\subset C_{\mathbf {x}}([0,T],{\mathbb {R}}^{d})\) of the path S.
Since \({\mathbb {P}}_{0,\mathbf {x}_{0}}\)-a.e. sample path belongs to  , Itô’s formula gives that \({\mathbb {P}}_{0,\mathbf {x}_{0}}\)-a.s.,
, Itô’s formula gives that \({\mathbb {P}}_{0,\mathbf {x}_{0}}\)-a.s.,
Localization as in (5.7) and using the fact that v ℓ ≥0 for all ℓ implies that
Applying once again the support theorem now yields a contradiction to the fact that v
k
(T
0,·)>0 in the open set U. This completes the proof for  .
.
Now we turn to the proof for  . In this case, the martingale problem for the operator
. In this case, the martingale problem for the operator  defined in (5.3) is well posed since the coefficients of
defined in (5.3) is well posed since the coefficients of  are again bounded and continuous (Stroock and Varadhan 1969). These properties of the coefficients also guarantee that the support theorem holds (Stroock and Varadhan 1972, Theorem 3.1). If \((\widetilde {\mathbb {P}}_{s,\mathbf {x}},\widetilde {\mathbf {X}})\) is a corresponding diffusion process, we can consider the laws of \(\mathbf {X}(t):=\exp (\widetilde {\mathbf {X}}(t))\) and, by Lemma 5.1, obtain a solution to the martingale problem for
are again bounded and continuous (Stroock and Varadhan 1969). These properties of the coefficients also guarantee that the support theorem holds (Stroock and Varadhan 1972, Theorem 3.1). If \((\widetilde {\mathbb {P}}_{s,\mathbf {x}},\widetilde {\mathbf {X}})\) is a corresponding diffusion process, we can consider the laws of \(\mathbf {X}(t):=\exp (\widetilde {\mathbf {X}}(t))\) and, by Lemma 5.1, obtain a solution to the martingale problem for  , which satisfies the support theorem with state space \({\mathbb {R}}^{d}_{+}\). We can now simply repeat the arguments from the proof for
, which satisfies the support theorem with state space \({\mathbb {R}}^{d}_{+}\). We can now simply repeat the arguments from the proof for  to also get the result for
to also get the result for  □
□
Proofs of the results from Section “Extension to functionally dependent strategies ”
Proof of Proposition 4.2.
The proof is analogous to the proof of Proposition 2.3. For  , all that is needed in addition to the arguments of Proposition 2.3 is the fact that the quadratic variation of
, all that is needed in addition to the arguments of Proposition 2.3 is the fact that the quadratic variation of
is given by
see (Schied and Voloshchenko 2016, Proposition 2.1). For  , the matrix a(s,S(s)) has to be replaced by the matrix with components a
ij
(s,S(s))S
i
(s)S
j
(s). □
, the matrix a(s,S(s)) has to be replaced by the matrix with components a
ij
(s,S(s))S
i
(s)S
j
(s). □
To prove Theorem 4.4 and Theorem 4.7 we need the following lemma, which is a straightforward extension of Lemma 5.1 to the functional setting. Its proof is therefore left to the reader. For X in the Skorohod space \(D([0,T],{\mathbb {R}}^{d})\) we set \(\left (\exp (\mathbf {X})\right)_{t} =\exp (\mathbf {X}_{t}):=\left (\exp (\mathbf {X}(u))\right)_{0\le u\le t}\in D([\!0,t],{\mathbb {R}}^{d}_{+})\).
Lemma 5.4.
The functional F t (X t ) solves (FTVP+) if and only if \(\widetilde {F}_{t}(\mathbf {X}_{t}):=F_{t}(\exp (\mathbf {X}_{t}))\) solves

where \(\widetilde {H}(\mathbf {X}_{T})=H(\exp (\mathbf {X}_{T}))\) and

where, as in (Cont and Fournié 2010, Eq. (15)), ∂ i are the partial vertical derivatives, \(\widetilde {a}_{ij}(t,\mathbf {X}(t)):=a_{ij}(t,\exp (\mathbf {X}(t)))\), and \(\widetilde {b}_{i}(t,\mathbf {X}(t)):=-\frac {1}{2} a_{ii}(t,\exp (\mathbf {X}(t)))\).
Note that the chain rule for functional derivatives (see (Dupire 2009, p.6)) implies the equivalence of the PDEs in \((\widetilde {\text {FTVP}})\) and (FTVP).
Regarding the regularity conditions in Definition 4.1, we note that \(\widetilde {F}\) will be regular enough if and only if F is regular enough (because exp(X(t)) is a sufficiently regular functional).
Proof of Theorem 4.4.
Part (a) directly follows from (Ji and Yang 2013, Theorem 20).
To prove part (b), note that the coefficients of  satisfy the conditions of (Ji and Yang 2013, Theorem 20), i.e., \(\widetilde {a}(t,\mathbf {X}(t))\) is positive definite and can be written as \(\widetilde {\sigma }(t,\mathbf {X}(t))\widetilde {\sigma }(t,\mathbf {X}(t))^{\top }\) with a Lipschitz continuous volatility coefficient \(\widetilde {\sigma },\) and \(\widetilde {b}_{i}\) is also Lipschitz. It therefore follows that \({(\widetilde {\text {FTVP}})}\) admits a unique solution \(\widetilde {F}\in \mathbb {C}^{1,2}([\!0,T))\) if \(\widetilde {H}\in C^{2}_{l,lip}(D([\!0,T],{\mathbb {R}}^{d})).\) Lemma 5.4 now establishes the existence of solutions to (FTVP+) if the terminal condition is of class \(C^{2}_{l,lip}(D([\!0,T],{\mathbb {R}}_{+}^{d}))\). □
satisfy the conditions of (Ji and Yang 2013, Theorem 20), i.e., \(\widetilde {a}(t,\mathbf {X}(t))\) is positive definite and can be written as \(\widetilde {\sigma }(t,\mathbf {X}(t))\widetilde {\sigma }(t,\mathbf {X}(t))^{\top }\) with a Lipschitz continuous volatility coefficient \(\widetilde {\sigma },\) and \(\widetilde {b}_{i}\) is also Lipschitz. It therefore follows that \({(\widetilde {\text {FTVP}})}\) admits a unique solution \(\widetilde {F}\in \mathbb {C}^{1,2}([\!0,T))\) if \(\widetilde {H}\in C^{2}_{l,lip}(D([\!0,T],{\mathbb {R}}^{d})).\) Lemma 5.4 now establishes the existence of solutions to (FTVP+) if the terminal condition is of class \(C^{2}_{l,lip}(D([\!0,T],{\mathbb {R}}_{+}^{d}))\). □
Proof of Theorem 4.7.
The proof is similar to the one of Theorem 3.3. We first consider the case of  . Let X and \({\mathbb {P}}_{t,\mathbf {x}}\) (0≤t≤T, \(\mathbf {x}\in {\mathbb {R}}^{d}\)) be as in the proof of Theorem 3.3. For a path \(\mathbf {Y}\in C([\!0,T],{\mathbb {R}}^{d})\), we define \(\overline {\mathbb {P}}_{t,\mathbf {Y}_{t}}\) as that probability measure on \(C([\!0,T],{\mathbb {R}}^{d})\) under which the coordinate process X satisfies \(\overline {\mathbb {P}}_{t,\mathbf {Y}_{t}}\)-a.s. X(s)=Y(s) for 0≤s≤t and under which the law of (X(u))
t≤u≤T
is equal to \({\mathbb {P}}_{t,\mathbf {Y}(t)}\). The support theorem (Stroock and Varadhan 1972, Theorem 3.1) then states that the law of (X(u))0≤u≤T
under \(\overline {\mathbb {P}}_{t,\mathbf {Y}_{t}}\) has full support on \(C_{\mathbf {Y}_{t}}([\!0,T],{\mathbb {R}}^{d}):=\{\boldsymbol {\omega } \in C([\!0,T],{\mathbb {R}}^{d})\,|\,\boldsymbol {\omega }_{t}=\mathbf {Y}_{t}\}\).
. Let X and \({\mathbb {P}}_{t,\mathbf {x}}\) (0≤t≤T, \(\mathbf {x}\in {\mathbb {R}}^{d}\)) be as in the proof of Theorem 3.3. For a path \(\mathbf {Y}\in C([\!0,T],{\mathbb {R}}^{d})\), we define \(\overline {\mathbb {P}}_{t,\mathbf {Y}_{t}}\) as that probability measure on \(C([\!0,T],{\mathbb {R}}^{d})\) under which the coordinate process X satisfies \(\overline {\mathbb {P}}_{t,\mathbf {Y}_{t}}\)-a.s. X(s)=Y(s) for 0≤s≤t and under which the law of (X(u))
t≤u≤T
is equal to \({\mathbb {P}}_{t,\mathbf {Y}(t)}\). The support theorem (Stroock and Varadhan 1972, Theorem 3.1) then states that the law of (X(u))0≤u≤T
under \(\overline {\mathbb {P}}_{t,\mathbf {Y}_{t}}\) has full support on \(C_{\mathbf {Y}_{t}}([\!0,T],{\mathbb {R}}^{d}):=\{\boldsymbol {\omega } \in C([\!0,T],{\mathbb {R}}^{d})\,|\,\boldsymbol {\omega }_{t}=\mathbf {Y}_{t}\}\).
Now suppose by way of contradiction that there exists an admissible arbitrage opportunity arising from a non-anticipative functional F as in Definition 4.6. In a first step, we show that F is nonnegative on \([0,T]\times C([0,T],{\mathbb {R}}^{d})\). As in the proof of Theorem 3.3, the support theorem implies that  is dense in \(C_{\mathbf {x}}([\!0,T],{\mathbb {R}}^{d})\). Condition (a) of Definition 3.2 and the left-continuity of F in the sense of (Cont and Fournié 2010, Definition 3) thus imply that F
T
(Y)≥0 for all \(\mathbf {Y}\in C([\!0,T],{\mathbb {R}}^{d})\). In the same way, we get from the admissibility of the arbitrage opportunity that F
t
(Y
t
)≥−c for all t∈[ 0,T] and \(\mathbf {Y}\in C([\!0,T],{\mathbb {R}}^{d})\). To show that actually F
t
(Y
t
)≥0, let \(Q\subset {\mathbb {R}}^{d}\) be a bounded domain whose closure is contained in \({\mathbb {R}}^{d}\) and let τ:= inf{s | X(s)∉Q} be the first exit time from Q. By the functional change of variables formula, in conjunction with the fact that F solves (FTVP) (on continuous paths), we obtain \(\overline {\mathbb {P}}_{t,\mathbf {Y}_{t}}\)-a.s. for t∈[0,T) that
is dense in \(C_{\mathbf {x}}([\!0,T],{\mathbb {R}}^{d})\). Condition (a) of Definition 3.2 and the left-continuity of F in the sense of (Cont and Fournié 2010, Definition 3) thus imply that F
T
(Y)≥0 for all \(\mathbf {Y}\in C([\!0,T],{\mathbb {R}}^{d})\). In the same way, we get from the admissibility of the arbitrage opportunity that F
t
(Y
t
)≥−c for all t∈[ 0,T] and \(\mathbf {Y}\in C([\!0,T],{\mathbb {R}}^{d})\). To show that actually F
t
(Y
t
)≥0, let \(Q\subset {\mathbb {R}}^{d}\) be a bounded domain whose closure is contained in \({\mathbb {R}}^{d}\) and let τ:= inf{s | X(s)∉Q} be the first exit time from Q. By the functional change of variables formula, in conjunction with the fact that F solves (FTVP) (on continuous paths), we obtain \(\overline {\mathbb {P}}_{t,\mathbf {Y}_{t}}\)-a.s. for t∈[0,T) that
By (Schied and Voloshchenko 2016, Proposition 2.1), we have
Since ∇
x
F and the coefficients of  are bounded in the closure of Q, the stochastic integral on the right-hand side of (5.9) is a true martingale. Therefore,
are bounded in the closure of Q, the stochastic integral on the right-hand side of (5.9) is a true martingale. Therefore,
Now let us take an increasing sequence Q 1⊂Q 2⊂⋯ of bounded domains exhausting \({\mathbb {R}}^{d}\) and whose closures are contained in \({\mathbb {R}}^{d}\). By τ n we denote the exit time from Q n . Then, an application of (5.10) for each τ n , Fatou’s lemma in conjunction with the fact that F≥−c, and the already established nonnegativity of F T (·) yield
This establishes the nonnegativity of F on \([\!0,T]\times C([\!0,T],{\mathbb {R}}^{d})\).
Now let  and T
0 be such that \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(0)\le 0\) and \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(T_{0})>0\). Since \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(t)=F_{t}(\mathbf {S}_{t})\) by Proposition 4.2, we have F
0(S
0)=0 and \(F_{T_{0}}(\mathbf {S}_{T_{0}})>0\). By left-continuity of F, we actually have \(F_{T_{0}}(\cdot)>0\) in an open neighborhood \(U\subset C_{\mathbf {S}(0)}([0,T],{\mathbb {R}}^{d})\) of the path S.
and T
0 be such that \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(0)\le 0\) and \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(T_{0})>0\). Since \(V^{\mathbf {S}}_{\boldsymbol {\xi }}(t)=F_{t}(\mathbf {S}_{t})\) by Proposition 4.2, we have F
0(S
0)=0 and \(F_{T_{0}}(\mathbf {S}_{T_{0}})>0\). By left-continuity of F, we actually have \(F_{T_{0}}(\cdot)>0\) in an open neighborhood \(U\subset C_{\mathbf {S}(0)}([0,T],{\mathbb {R}}^{d})\) of the path S.
Since \({\mathbb {P}}_{0,\mathbf {S}(0)}\)-a.e. sample path belongs to  , the functional change of variables formula gives that \({\mathbb {P}}_{0,\mathbf {S}(0)}\)-a.s.,
, the functional change of variables formula gives that \({\mathbb {P}}_{0,\mathbf {S}(0)}\)-a.s.,
Localization as in (5.11) and using the fact that F≥0 implies that
Applying once again the support theorem now yields a contradiction to the fact that \(F_{T_{0}}(\cdot)>0\) in the open set U. This completes the proof for  .
.
The proof for  is completed by an exponential transformation, as in the proof of Theorem 3.3. □
is completed by an exponential transformation, as in the proof of Theorem 3.3. □
References
Acciaio, B, Beiglböck, M, Penkner, F, Schachermayer, W: A model-free version of the fundamental theorem of asset pricing and the super-replication theorem. Math. Finance. 26(2), 233–251 (2016). doi:10.1111/mafi.12060.
Alvarez, A, Ferrando, S, Olivares, P: Arbitrage and hedging in a non probabilistic framework. Math. Financ. Econ. 7(1), 1–28 (2013). doi:10.1007/s11579-012-0074-5.
Beiglböck, M, Cox, AM, Huesmann, M, Perkowski, N, Prömel, DJ: Pathwise super-replication via Vovk’s outer measure (2015). http://arxiv.org/abs/1504.03644.
Bender, C, Sottinen, T, Valkeila, E: Pricing by hedging and no-arbitrage beyond semimartingales. Finance Stoch. 12(4), 441–468 (2008). doi:10.1007/s00780-008-0074-8.
Biagini, S, Bouchard, B, Kardaras, C, Nutz, M: Robust fundamental theorem for continuous processes. Mathematical Finance (2015). doi:10.1111/mafi.12110.
Bick, A, Willinger, W: Dynamic spanning without probabilities. Stochastic Process. Appl. 50(2), 349–374 (1994). doi:10.1016/0304-4149(94)90128-7.
Bouchard, B, Nutz, M: Arbitrage and duality in nondominated discrete-time models. Ann. Appl. Probab. 25(2), 823–859 (2015). doi:10.1214/14-AAP1011.
Bühler, H: Pricing with a discrete smile (2015). SSRN preprint 2642630 http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2642630.
Cont, R, Fournié, D-A: Change of variable formulas for non-anticipative functionals on path space. J. Funct. Anal. 259(4), 1043–1072 (2010). doi:10.1016/j.jfa.2010.04.017.
Davis, M, Obłój, J, Raval, V: Arbitrage bounds for prices of weighted variance swaps. Math. Finance. 24(4), 821–854 (2014). doi:10.1111/mafi.12021.
Dudley, RM: Wiener functionals as Itô integrals. Ann. Probability. 5(1), 140–141 (1977).
Dupire, B: Pricing and hedging with smiles. In: Mathematics of Derivative Securities (Cambridge, 1995), Publ. Newton Inst, pp. 103–111. Cambridge Univ. Press, Cambridge (1997).
Dupire, B: Functional Itô calculus. Bloomberg Portfolio Research Paper (2009).
El Karoui, N, Jeanblanc-Picqué, M, Shreve, SE: Robustness of the Black and Scholes formula. Math. Finance. 8(2), 93–126 (1998). doi:10.1111/1467-9965.00047.
Föllmer, H: Calcul d’Itô sans probabilités. In: Seminar on Probability, XV (Univ. Strasbourg, Strasbourg, 1979/1980), Lecture Notes in Math, pp. 143–150. Springer, Berlin (1981).
Föllmer, H: Probabilistic aspects of financial risk. In: European Congress of Mathematics, Vol. I (Barcelona, 2000), Progr. Math, pp. 21–36. Birkhäuser, Basel (2001).
Föllmer, H, Schied, A: Stochastic Finance. An Introduction in Discrete Time. 3rd ed. Walter de Gruyter & Co., Berlin (2011).
Freedman, D: Brownian Motion and Diffusion. 2nd ed. Springer, New York (1983).
Hobson, D: The Skorokhod embedding problem and model-independent bounds for option prices. In: Paris-Princeton Lectures on Mathematical Finance 2010, Lecture Notes in Math, pp. 267–318. Springer (2011), doi:10.1007/978-3-642-14660-2_4 http://dx.doi.org/10.1007/978-3-642-14660-2_4.
Hobson, DG: Robust hedging of the lookback option. Finance Stoch. 2(4), 329–347 (1998).
Janson, S, Tysk, J: Preservation of convexity of solutions to parabolic equations. J. Differential Equations. 206(1), 182–226 (2004). doi:10.1016/j.jde.2004.07.016.
Jeanblanc, M, Yor, M, Chesney, M: Mathematical Methods for Financial Markets. Springer Finance. Springer (2009).
Ji, S, Yang, S: Classical solutions of path-dependent PDEs and functional forward-backward stochastic systems. Math. Probl. Eng, 423101–11 (2013). downloads.hindawi.com/journals/mpe/2013/423101.pdf.
Lyons, TJ: Uncertain volatility and the risk-free synthesis of derivatives. Appl. Math. Finance. 2(2), 117–133 (1995).
Peng, S, Wang, F: BSDE, path-dependent PDE and nonlinear Feynman-Kac formula. F. Sci. China Math. 59, 19 (2016). doi:10.1007/s11425-015-5086-1.
Riedel, F: Financial economics without probabilistic prior assumptions. Decisions Econ. Finan. 38, 75–91 (2015). doi:10.1007/s10203-014-0159-0.
Schied, A: Model-free CPPI. J. Econom. Dynam. Control. 40, 84–94 (2014). doi:10.1016/j.jedc.2013.12.010.
Schied, A: On a class of generalized Takagi functions with linear pathwise quadratic variation. J. Math. Anal. Appl. 433, 974–990 (2016).
Schied, A, Stadje, M: Robustness of delta hedging for path-dependent options in local volatility models. J. Appl. Probab. 44(4), 865–879 (2007). doi:10.1239/jap/1197908810.
Schied, A, Voloshchenko, I: The associativity rule in pathwise functional Itô calculus (2016). http://arxiv.org/abs/1605.08861.
Schied, A, Speiser, L, Voloshchenko, I: Model-free portfolio theory and its functional master formula (2016). arXiv preprint 1606.03325.
Sondermann, D: Introduction to Stochastic Calculus for Finance. Lecture Notes in Economics and Mathematical Systems, Vol. 579. Springer, Berlin (2006).
Stroock, DW, Varadhan, SRS: Diffusion processes with continuous coefficients. Comm. Pure Appl. Math. 22, 345–400479530 (1969).
Stroock, DW, Varadhan, SRS: On the support of diffusion processes with applications to the strong maximum principle. In: Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability (Univ. California, Berkeley, Calif., 1970/1971), Vol. III: Probability theory, pp. 333–359. Univ. California Press, Berkeley, Calif (1972).
Vovk, V: Rough paths in idealized financial markets. Lith. Math. J. 51(2), 274–285 (2011). doi:10.1007/s10986-011-9125-5.
Vovk, V: Continuous-time trading and the emergence of probability. Finance Stoch. 16(4), 561–609 (2012). doi:10.1007/s00780-012-0180-5.
Vovk, V: Itô calculus without probability in idealized financial markets. Lith. Math. J. 55(2), 270–290 (2015). doi:10.1007/s10986-015-9280-1.
Widder, DV: The Heat Equation. Pure and Applied Mathematics, Vol. 67, pp. 267, New York and London (1975).
Acknowledgements
The authors thank Li Chen and Martin U. Schmidt for helpful comments and gratefully acknowledge support by Deutsche Forschungsgemeinschaft through the Research Training Group RTG 1953.
Authors’ contributions
Both authors contributed equally to the results; and read and approved the final manuscript.
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Schied, A., Voloshchenko, I. Pathwise no-arbitrage in a class of Delta hedging strategies. Probab Uncertain Quant Risk 1, 3 (2016). https://doi.org/10.1186/s41546-016-0003-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41546-016-0003-2
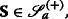 , there exists a basic admissible integrand ξ
S on [ r,u] such that
, there exists a basic admissible integrand ξ
S on [ r,u] such that
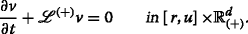
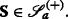 .
.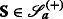 for which
for which 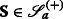 and t
and t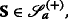 , there exists a general admissible integrand ξ
S on [r,u] such that
, there exists a general admissible integrand ξ
S on [r,u] such that
