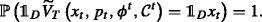- Research
- Open access
- Published:
Arbitrage-free pricing of derivatives in nonlinear market models
Probability, Uncertainty and Quantitative Risk volume 3, Article number: 2 (2018)
Abstract
The objective of this paper is to provide a comprehensive study of the no-arbitrage pricing of financial derivatives in the presence of funding costs, the counterparty credit risk and market frictions affecting the trading mechanism, such as collateralization and capital requirements. To achieve our goals, we extend in several respects the nonlinear pricing approach developed in (El Karoui and Quenez 1997) and (El Karoui et al. 1997), which was subsequently continued in (Bielecki and Rutkowski 2015).
1 Introduction
The paper contributes to the nonlinear arbitrage-free pricing theory, which arises in a natural way due to the salient features of real-world trades, such as: trading constraints, differential funding costs, collateralization, counterparty credit risk, and capital requirements. Our aim is to extend in several respects the nonlinear hedging and pricing approach developed in El Karoui and Quenez (1997) and El Karoui et al. (1997) who used a BSDE approach, by accounting for the complexity of over-the-counter financial derivatives and specific features of the trading environment after the global financial crisis. This work builds also upon the earlier paper by (Bielecki and Rutkowski 2015) where, however, the important issue of no-arbitrage was not studied in depth. The paper is structured as follows:
-
In Section 2, we introduce the self-financing trading strategies in the presence of differential funding rates and adjustment processes. We consider general contracts with cash flow streams, rather than simple contingent claims with a single payoff either at the contract’s maturity or upon early exercise. We also introduce in Section 2.9 the concepts of local and global valuation problems. This distinction is crucial since it demonstrates that results obtained in Sections 3 and 4 are capable of covering also financial models and valuation problems that cannot be addressed through classical BSDEs, which are nowadays commonly used to deal with nonlinear financial markets.
-
Section 3 is devoted to a comprehensive examination of the issue of existence of arbitrage opportunities for the hedger and for the trading desk in a nonlinear trading framework and with respect to a predetermined class of contracts. We introduce the concept of no-arbitrage with respect to the null contract and a stronger notion of no-arbitrage for the trading desk. We then proceed to the issue of unilateral fair valuation of a given contract by the hedger who is endowed with an initial capital. We examine the link between the concept of no-arbitrage for the trading desk and the financial viability of prices computed by the hedger.
-
In Section 4, we propose and analyze the concept of a regular market model, which can be seen as an extension of the notion of a nonlinear pricing system, which was introduced by (El Karoui and Quenez 1997). The goal is to identify a class of nonlinear market models, which are arbitrage-free for the trading desk and, in addition, enjoy the desirable property that if a given contract can be replicated, then the cost of replication is also the fair price for the hedger.
-
Section 5 focuses on replication of a contract in a regular market model. We propose four alternative definitions of no-arbitrage prices, namely, the gained value, the ex-dividend price, the exit price, and the offsetting price. Generally speaking, it is not expected that these prices will coincide, since they correspond to different valuation problems for the hedger. However, when the trading arrangements in the underlying model are such that the valuation problem is local then, under some suitable technical conditions, we show that the gained value and the ex-dividend price coincide.
-
In Section 6, we present a BSDEs approach to the valuation and hedging and derive examples of BSDEs for the gained value and the ex-dividend price. Finally, we briefly address in Section 7 the issue of the so-called valuation adjustments in linear and nonlinear market models and we make some comments on the prevailing market practice of separation of ‘clean price’ from the ‘total valuation adjustment’.
Although we focus on the issue of fair unilateral valuation from the perspective of the hedger, it is clear that identical definitions and valuation methods are applicable to his counterparty as well. Hence, in principle, it is possible to use our results to examine the interval of fair bilateral prices in a regular market model. Particular instances of such unilateral and bilateral valuation problems were previously studied in Nie and Rutkowski (2015, 2016a, 2017 (published online on 18 April 2017)) where it was shown that a non-empty interval of either fair bilateral prices or bilaterally profitable prices can be obtained in some nonlinear models for contracts with either an exogenous or an endogenous collateralization. It should be acknowledged that there exists a vast body of literature devoted to valuation and hedging of financial derivatives under differential funding costs, collateralization, the counterparty credit risk and other trading adjustments (see, for instance, Bichuch et al. (2018), Brigo and Pallavicini (2014), Brigo et al. (2018, 2017), Burgard and Kjaer (2011, 2013), Crépey (2015a, b), Mercurio (2013), Pallavicini et al. (2012b, a), and Piterbarg (2010). In view of limited space, we cannot present here these works in detail. Let us only mention that most of these papers deal with linear market models of credit risk (possibly also with differential funding rates), whereas the general theory developed in this work aims to address problems where the emphasis is put on a nonlinear character of valuation in market models with imperfections. In contrast, Albanese et al. (2017), Albanese and Crépey (2017), and Crépey et al. (2017) propose to address the issue of valuation adjustments through an alternative approach, which is based on the global valuation paradigm referencing to the balance sheet of the bank, its internal structure, and long-term interests of bank’s shareholders. The issue of nonlinearity of trading does not appear in their approach, since the classical hedging arguments are no longer employed to determine the value of a new contract, which is added to the existing portfolio of bank’s assets. For further comments on some of the above-mentioned papers, we refer to Section 7.
2 Nonlinear market model
We start by re-examining and extending the nonlinear trading setup introduced in Bielecki and Rutkowski (2015). Throughout the paper, we fix a finite trading horizon date T>0 for our market model. Let \((\Omega, \mathcal {G}, \mathbb {G}, \mathbb {P})\) be a filtered probability space satisfying the usual conditions of right-continuity and completeness, where the filtration \(\mathbb {G}=(\mathcal {G}_{t})_{t \in [0,T]}\) models the flow of information available to the hedger and his counterparty. For convenience, we assume that the initial σ-field \({\mathcal {G}}_{0}\) is trivial. All processes introduced in what follows are implicitly assumed to be \(\mathbb {G}\)-adapted and, as usual, any semimartingale is assumed to be a càdlàg process. Let us introduce the notation for the prices of all traded assets in our model.
Risky assets. We denote by \(\mathcal {S}=\left (S^{1},\ldots,S^{d}\right)\) the collection of the ex-dividend prices of a family of d risky assets with the corresponding cumulative dividend streams\(\mathcal {D} =\left (D^{1},\ldots, D^{d}\right)\). The process Si represents the ex-dividend price of any traded security, such as, stock, sovereign or corporate bond, stock option, interest rate swap, currency option or swap, credit default swap, etc.
Funding accounts. We denote by Bi,l (resp. Bi,b) the lending (resp. borrowing) funding account associated with the ith risky asset, for i=1,2,…,d. The financial interpretation of these accounts varies from case to case. For an overview of trading mechanisms for risky assets, we refer to Section 2.6. In the special case when Bi,l=Bi,b, we will use the notation Bi and we call it the funding account for the ith risky asset.
Cash accounts. The lending cash account B0,l and the borrowing cash account B0,b are used for unsecured lending and borrowing of cash, respectively. For brevity, we will sometimes write Bl and Bb instead of B0,l and B0,b. Also, when the borrowing and lending cash rates are equal, the single cash account is denoted by B0 or, simply, B. Note, however, that since an unlimited borrowing/depositing of cash in the bank account is not a realistic feature of a trading model, it is not assumed in what follows.
For brevity, we denote by \(\mathcal {B} =(B^{i,l},B^{i,b},\ i=0,1,\ldots,d)\) the collection of all cash and funding accounts.
2.1 Contracts with trading adjustments
We will consider financial contracts between two parties, called the hedger and the counterparty. In what follows, all the cash flows will be viewed from the prospective of the hedger, with the convention that a positive cash flow means that the hedger receives the corresponding amount, and a negative cash flow meaning that the hedger makes a payment. A bilateral financial contract (or simply a contract) is given as a pair \(\mathcal {C}=(A,\mathcal {X})\), where the meaning of each term is explained below.
A stochastic processes A represents the cumulative cash flows from time 0 till the contracts’s maturity date, which is denoted as T. In the financial interpretation, the process A is assumed to model the cumulative (promised) cash flows of a given contract, which are either paid out from the hedger’s wealth or added to his wealth via the value process of his portfolio of traded assets (including positive or negative holdings of cash, that is, lent or borrowed money). Note that the price of the contract \(\mathcal {C}\) exchanged at its initiation (that is, at time 0) is not included in A. For example, if the contract stipulates that the hedger will ‘receive’ the (possibly random and of arbitrary signs) cash flows \(a_{1},a_{2},\dots,a_{m}\) at times \(t_{1},t_{2},\dots,t_{m} \in (0,T]\), then A is given by

Let (At,0) denote a basic contract originated at time t with \(\mathcal {X} =0\). Then the only cash flow exchanged between the counterparties at time t is the price of the contract and thus the remaining cumulative cash flows of (At,0) are given as \(A^{t}_{u} := A_{u}-A_{t}\) for u∈[t,T]. In particular, the equality \(A^{t}_{t}=0\) is valid for any basic contract (A,0) and any date t∈[0,T). All future cash flows a l for l such that t l >t are predetermined, in the sense that they are explicitly specified by the contract covenants.
As a simple example of cash flows, consider the situation where the hedger sells at time t the European call option on the risky asset Si. Then m=1, t1=T, and the terminal payoff from the perspective of the hedger equals \(a_{1}=- \left (S^{i}_{T}-K\right)^{+}\). More generally, for every t∈[0,T), the process At is given by  for every u∈[t,T].
for every u∈[t,T].
To account for additional features of a particular contract at hand, we find it convenient to postulate that the cash flows A (resp. At) of a basic contract are complemented by trading adjustments, which are represented by the process \(\mathcal {X}\) (resp. \(\mathcal {X}^{t}\)) given as \(\mathcal {X}=\left (X^{1},\ldots, X^{n}; \alpha ^{1}, \ldots, \alpha ^{n}; \beta ^{1}, \ldots, \beta ^{n}\right).\) The role of \(\mathcal {X}\) is to describe additional clauses of a given contract, such as rehypothecated or segregated collateral, as well as to account for the impact of atypical trading arrangements on the value process of the hedger’s portfolio. For each adjustment process Xk, the process αkXk represents additional incoming or outgoing cash flows for the hedger, which are either stipulated in the clauses of the contract or imposed by a third party (for instance, the regulator). For each process Xk, k=1,2,…,n we also specify the remuneration process βk, which is used to determine the net interest payments (if any) associated with the process Xk. It should be noted that the processes \(X^{1}, \dots, X^{n}\) and the associated remuneration processes \(\beta ^{1}, \dots, \beta ^{n}\) do not represent traded assets. It is rather clear that the processes α and β may depend on the respective adjustment process. Therefore, when the adjustment process is \(\mathcal {Y}\), rather than \(\mathcal {X}\), one should write \(\alpha (\mathcal {Y})\) and \(\beta (\mathcal {Y})\) in order to avoid confusion. However, for brevity, we will keep the shorthand notation α and β when the adjustment process is denoted as \(\mathcal {X}\). For further comments on trading adjustment, we refer to Section 2.3 and 2.4. Last, but not least, we will need to define a suitable modification of the promised cash flows A resulting from the counterparty credit risk (see Definition 5 where the concept of counterparty risky cumulative cash flows is introduced).
In essence, by valuation of a given contract we mean the process of finding at any date t the range of the fair prices p t , as seen from the viewpoint of either the hedger or the counterparty. Although it will be postulated that the two parties in a contract adopt the same valuation paradigm, due to the asymmetry of cash flows, differential trading costs, and possibly also different trading opportunities, they will typically obtain different ranges for the respective fair unilateral prices for a given bilateral contract. Let us stress that the disparity in unilateral valuation done by the two parties is a consequence of the nonlinearity of the wealth dynamics in trading strategies, so that it will typically occur even within the framework of a complete nonlinear model where the perfect replication of any contract can be achieved by the counterparties. The important issue of determining the range of fair bilateral prices in a general nonlinear framework is left for a future research (for results on bilateral pricing in some specific nonlinear models, we refer to Nie and Rutkowski (2015, 2016a, 2018).
2.2 Self-financing trading strategies
The concept of a portfolio refers to the family of primary traded assets, that is, risky assets, cash accounts, and funding accounts for risky assets. Formally, by a portfolio on the time interval [t,T], we mean an arbitrary \({\mathbb R}^{3d+2}\)-valued, \(\mathbb {G}\)-adapted process \((\phi ^{t}_{u})_{u \in [t,T]}\) denoted as
where the components represent the positions in risky assets \(\left (S^{i},D^{i}\right),\, i=1,2, \dots, d\), cash accounts B0,l, B0,b, and funding accounts \(B^{i,l},B^{i,b},\, i=1,2, \dots, d\) for risky assets. It is postulated throughout that \(\psi ^{j,l}_{u} \geq 0,\, \psi ^{j,b}_{u} \leq 0\) and \(\psi ^{j,l}_{u} \psi ^{j,b}_{u} =0\) for all \(j=0,1, \dots,d\) and u∈[t,T]. If the borrowing and lending rates are equal, then we write ψj=ψj,l+ψj,b. It is also assumed throughout that the processes ξ1,…,ξd are \(\mathbb {G}\)-predictable.
We say that a portfolio ϕ is constrained if at least one of the components of the process ϕ is assumed to satisfy some explicitly stated constraints, which directly affect the choice of ϕ. For instance, we will need to impose conditions ensuring that the funding of each risky asset is done using the corresponding funding account. Another example of an explicit constraint is obtained when we set \(\psi ^{0,b}_{u} =0\) for all u∈[t,T], meaning that an outright borrowing of cash from the account B0,b is prohibited. For examples of markets with various kinds of portfolio constraints, we refer to Carassus et al. (2001), Fahim and Huang (2016), Karatzas and Kou (1996,1998), and Pulido (2014) and the references therein. The concept of a constrained portfolio should be contrasted with the notion of admissibility of a trading strategy that may involve some additional conditions imposed on the wealth process and thus indirectly also on the class of admissible processes ϕ (see Definition 8). Note that portfolio constraints are not a matter of choice, since they are due to genuine real-life restrictions imposed on traders. This should be contrasted with the idea of admissibility of a trading strategy, which is a mathematical artefact needed to preclude unrealistic arbitrage opportunities (like doubling strategies), which may be present within a stochastic model when continuous trading is allowed. Note in this regard that there is no need to be concerned with the admissibility under the realistic assumption that only a finite number of trading times is available to traders.
We are now in a position to state some standard technical assumptions underpinning our further developments.
Assumption 1
We work throughout under the following standing assumptions:
-
(i)
for every \(i=1,2,\dots, d\), the price Si of the ith risky asset is a semimartingale and the cumulative dividend stream Di is a process of finite variation with \(D^{i}_{0}=0\);
-
(ii)
the cash and funding accounts Bj,l and Bj,b are strictly positive and continuous processes of finite variation with \(B^{j,l}_{0}=B^{j,b}_{0}=1\) for j=0,1,…,d;
-
(iii)
the cumulative cash flow process A of any contract is a process of finite variation;
-
(iv)
the adjustment processes Xk, k=1,2,…,n and the auxiliary processes αk, k=1,2,…,n are semimartingales;
-
(v)
the remuneration processes βk, k=1,2,…,n are strictly positive and continuous processes of finite variation with \(\beta ^{k}_{0}=1\) for every k.
In the next definition, the \(\mathcal {G}_{t}\)-measurable random variable x
t
represents the endowment of the hedger at time t∈[0,T) whereas p
t
, which at this stage is an arbitrary \(\mathcal {G}_{t}\)-measurable random variable, stands for the price at time t of \(\mathcal {C}^{t}=\left (A^{t},\mathcal {X}^{t}\right)\), as seen by the hedger. Recall that At denotes the cumulative cash flows of the contract A that occur after time t, that is, \(A^{t}_{u}:=A_{u}-A_{t}\) for all u∈[t,T]. Hence At can be seen as a contract with the same remaining cash flows as the original contract A, except that At starts and is traded at time t. By the same token, we denote by \(\mathcal {X}^{t}\) the adjustment process related to the contract At. Let  be a predetermined class of contracts. As expected, it is assumed throughout that the null contract \(\mathcal {N}=(0,0)\) is traded in any market model at any time t, that is,
be a predetermined class of contracts. As expected, it is assumed throughout that the null contract \(\mathcal {N}=(0,0)\) is traded in any market model at any time t, that is,  for every t∈[0,T) (see Assumption 3).
for every t∈[0,T) (see Assumption 3).
It should be noted that the prices p
t
for contracts belonging to the class  are yet unspecified and thus there is a certain degree of freedom in the foregoing definitions. Note also that we use the convention that \(\int _{t}^{u}:=\int _{(t,u]}\) for any t≤u.
are yet unspecified and thus there is a certain degree of freedom in the foregoing definitions. Note also that we use the convention that \(\int _{t}^{u}:=\int _{(t,u]}\) for any t≤u.
Definition 1
A quadruplet \(\left (x_{t},p_{t},\phi ^{t},\mathcal {C}^{t}\right)\) is a self-financing trading strategy on [t,T] associated with the contract \(\mathcal {C}=(A,\mathcal {X})\) if the portfolio value\(V^{p} \left (x_{t},p_{t},\phi ^{t},\mathcal {C}^{t}\right)\), which is given by
satisfies for all u∈[t,T]
where the adjusted gains process\(G\left (x_{t},p_{t},\phi ^{t},\mathcal {C}^{t}\right)\) is given by
For a given pair (x t ,p t ), we denote by \(\Phi ^{t,x_{t}}\left (p_{t},\mathcal {C}^{t}\right)\) the set of all self-financing trading strategies on [t,T] associated with the contract \(\mathcal {C}\).
When studying valuation of the contract \(\mathcal {C}^{t}\) for a fixed t, we will typically assume that the hedger’s endowment x
t
is given and we will search for the range of hedger’s fair prices p
t
for \(\mathcal {C}^{t}\). Therefore, when dealing with the hedger with a fixed initial endowment x
t
at time t, we will consider the following set of self-financing trading strategies  Note, however, that the definition of the market model does not assume that the quantity x
t
is predetermined.
Note, however, that the definition of the market model does not assume that the quantity x
t
is predetermined.
Definition 2
The market model is the quintuplet  where
where  stands for the set of all self-financing trading strategies associated with the class
stands for the set of all self-financing trading strategies associated with the class  of contracts, that is,
of contracts, that is, 
In principle, the market model defined above exhibits nonlinear features, in the sense that either the portfolio value process \(V^{p}(x_{t},p_{t},\phi ^{t},\mathcal {C}^{t})\) is not linear in \((x_{t}, p_{t},\phi ^{t},\mathcal {C}^{t})\) or the class of all self-financing strategies is not a vector space (or, typically, both). Therefore, we refer to this setup as to a generic nonlinear market model. In contrast, by a linear market model we will understand in this paper the version of the model defined above in which all trading adjustments are null (i.e., Xk=0 for all \(k=1,2, \dots, n\)), there are no differential funding rates (i.e., Bj,b=Bj,l for all \(j=0,1, \dots, d\)) and no portfolio constraints are imposed. In particular, in the linear market model the class of all self-financing trading strategies is a vector space and the value process \(V^{p}\left (x_{t},p_{t},\phi ^{t},\mathcal {C}^{t}\right)\) is a linear mapping in \(\left (x_{t},p_{t},\phi ^{t},\mathcal {C}^{t}\right)\). Note, however, that the last property is usually lost when an admissibility condition is imposed on the class of trading strategies since, typically, a trading strategy is deemed to be admissible if it its discounted wealth is bounded from below or nonnegative (hence the class of admissible trading strategies is no longer a vector space).
To alleviate notation, we will frequently write \((x,p,\phi,\mathcal {C})\) instead of \(\left (x_{0},p_{0},\phi ^{0},\mathcal {C}^{0}\right)\) when working on the interval [0,T]. Note that (2)–(4) yield the following equalities for any trading strategy 
Recall that in the classical case of a frictionless market, it is common to assume that the initial endowments of traders are null. Moreover, the price of a derivative has no impact on the dynamics of the gains process. In contrast, when portfolio’s value is driven by nonlinear dynamics, the initial endowment x at time 0, the initial price p and the adjustment cash flows of a contract may all affect the dynamics of the gains process and thus the classical approach is no longer valid.
2.3 Funding adjustment
The concept of the funding adjustment refers to the spreads of funding rates with regard to some benchmark cash rate. In the present setup, it can be defined relative to either Bl or Bb. If the lending and borrowing rates are not equal, then (3) can be written as follows
where \(\widehat {B}^{j,l/b} := B^{j,l/b} \left (B^{0,l/b}\right)^{-1}\) and \(\widehat {\beta }^{k,l/b} := \beta ^{k}\left (B^{0,l/b}\right)^{-1} \). The quantity
is called the funding adjustment. If the borrowing and lending rates are equal, then the expression for the funding adjustment simplifies to
When the cash account B0 is used for funding and remuneration for adjustment processes, that is, when Bi=B0 for i=1,2,…,d and βk=B0 for k=1,2,…,n, then the funding adjustment vanishes, as was expected.
2.4 Financial interpretation of trading adjustments
In this study, we will devote significant attention to terms appearing in the dynamics of \(V^{p}(x,\varphi,A,\mathcal {X})\), which correspond to the trading adjustment process \(\mathcal {X}\).
Definition 3
The stochastic process \(\varpi =\sum _{k=1}^{n} \varpi ^{k} \), where for k=1,2,…,n,
is called the cash adjustment.
In general, the financial interpretation of the cash adjustment term ϖk is as follows: the term \(\alpha ^{k}_{t}X^{k}_{t}\) represents the part of the kth adjustment that the hedger can either use for his trading purposes when \(\alpha ^{k}_{t} X^{k}_{t} >0\) or has to put aside (for instance, pledge to his counterparty as a collateral or hold in a separate account as a regulatory capital) when \(\alpha ^{k}_{t} X^{k}_{t} <0\). Formally, the quantity \(-X_{t}^{k} \left (\beta ^{k}_{t}\right)^{-1}\) can be seen as the number of “shares” of the remuneration process βk that the hedger should hold at time t in order to cover interest payments associated with the adjustment process Xk. Hence the integral \(\int _{0}^{t} X_{u}^{k} \left (\beta ^{k}_{u}\right)^{-1}\, d\beta ^{k}_{u}\) represents the cumulative interest either paid or received by the hedger due to the presence of the kth trading adjustment.
Let us illustrate a few alternative interpretations of cash adjustments given by (6). We hereafter write \(\widehat {X}^{k}=\left (\beta ^{k}\right)^{-1} X^{k} \).
-
Let us first assume that \(\alpha ^{k}_{t}=1\), for all t. The term \(X^{k}_{t}-\int _{0}^{t} \widehat {X}^{k}_{u}\, d\beta ^{k}_{u}\) indicates that the cash adjustment ϖk is affected by both the current value \(X^{k}_{t}\) of the adjustment process and by the cost of funding of this adjustment given by the integral \(\int _{0}^{t} \widehat {X}^{k}_{u}\, d\beta ^{k}_{u}\). Such a situation occurs, for example, when Xk represents the capital charge or the rehypotecated collateral. The integration by parts formula gives
$$ \varpi^{k}_{t} = X^{k}_{t}-\int_{0}^{t} \widehat{X}^{k}_{u}\, d\beta^{k}_{u}=X^{k}_{0}+\int_{0}^{t}\, \beta^{k}_{u}\, d\widehat{X}^{k}_{u}, $$(7)where the integral \(\int _{0}^{t} \beta ^{k}_{u}\,d\widehat {X}^{k}_{u}\) has the following financial interpretation: \(\widehat {X}^{k}_{u}\) is the number of units of the funding account \(\beta ^{k}_{u}\) that are needed to fund the amount \(X^{k}_{u}\) of the adjustment process. Hence \(d\widehat {X}^{k}_{u}\) is the infinitesimal change of this number and \(\beta ^{k}_{u}\,d\widehat {X}^{k}_{u}\) is the cost of this change, which has to be absorbed by the change in the value of the trading strategy. Observe that the term \(\beta ^{k}_{u}\,d\widehat {X}^{k}_{u}\) may be negative, meaning that a cash relieve situation is taking place.
-
In the special case when \(\alpha ^{k}_{t}=1\) and \(\beta ^{k}_{t}=1\) for all t, we obtain \(\varpi ^{k}_{t}=X^{k}_{t}\) for all t. We deal here with the cash adjustment Xk on which there is no remuneration since manifestly \(\int _{0}^{t} \widehat {X}^{k}_{u}\,d\beta ^{k}_{u}=0.\) This situation may arise, for example, if the bank does not use any external funding for financing this adjustment, but relies on its own cash reserves, which are assumed to be kept idle and neither yield interest nor require interest payouts.
-
Let us now assume that \(\alpha ^{k}_{t}=0\) for all t. Then the term \( \varpi ^{k}_{t}=- \int _{0}^{t} \widehat {X}^{k}_{u}\, d\beta ^{k}_{u}\) indicates that the cash value of the adjustment Xk does not contribute to the portfolio value. Only the remuneration of the adjustment process Xk, which is given by the integral \(\int _{0}^{t} \widehat {X}^{k}_{u}\, d\beta ^{k}_{u}\), contributes to the portfolio’s value. This happens, for example, when the adjustment process represents the collateral posted by the counterparty and kept in the segregated account.
The above considerations lead to the following lemma, which gives a convenient representation for the cash adjustment process when αk is equal to either 1 or 0. In most practical situations, a general case can also be dealt with using Lemma 1 and a suitable redefinition of adjustment processes.
Lemma 1
Let the non-negative integers n1,n2,n3 be such that n1+n2+n3=n. If αk=1 for \(k=1,2,\dots, n_{1}+n_{2}\), βk=1 for \(k=n_{1}, n_{1}+1, \dots, n_{1}+n_{2}\) and αk=0 for \(k=n_{1}+n_{2}, n_{1}+n_{2}+1, \dots, n_{1}+n_{2}+n_{3}\), then the cash adjustment process ϖ satisfies, for all t∈[0,T],
2.5 Wealth process
Let \((x, p,\phi,\mathcal {C})\) be an arbitrary self-financing trading strategy. Then the following natural question arises: what is the wealth of a hedger at time t, say \(V_{t}(x, p,\phi,\mathcal {C})\)? It is clear that if the hedger’s initial endowment equals x, then his initial wealth equals x+p when he sells a contract \(\mathcal {C} \) at the price p at time 0. By contrast, the initial value of the hedger’s portfolio, that is, the total amount of cash he invests at time 0 in his portfolio of traded assets, is given by (5) meaning that the trading adjustments at time 0 need to be accounted for in the initial portfolio’s value. However, according to the financial interpretation of trading adjustments, they have no bearing on the hedger’s initial wealth and thus the relationship between the hedger’s initial wealth and the initial portfolio’s value reads
Analogous arguments can be used at any time t∈[0,T], since the hedger’s wealth at time t should represent the value of his portfolio of traded assets net of the value of all trading adjustments (see (10)). Furthermore, one needs to focus on the actual ownership (as opposed to the legal ownership) of each of the adjustment processes \(X^{1}, \dots, X^{n}\), of course, provided that they do not vanish at time t. Although this general rule is cumbersome to formalize, it will not present any difficulties when applied to a particular contract at hand.
For instance, in the case of the rehypothecated cash collateral (see Section 2.7.1), the hedger’s wealth at time t should be computed by subtracting the collateral amount C t from the portfolio’s value. This is consistent with the actual ownership of the cash amount delivered by either the hedger or the counterparty at time t. For example, if \(C^{+}_{t}>0\) then the legal owner of the amount \(C^{+}_{t}\) at time t could be either the hedger or the counterparty (depending on the legal covenants of the collateral agreement) but the hedger, as a collateral taker, is allowed to use the collateral amount for his trading purposes. If there is no default before T, the collateral taker returns the collateral amount to the collateral provider. Hence the amount \(C^{+}_{t}\) should be accounted for when dealing with the hedger’s portfolio, but should be excluded from his wealth. In general, we have the following definition of the wealth process.
Definition 4
The wealth process of a self-financing trading strategy \((x_{t}, p_{t},\phi ^{t},\mathcal {C}^{t})\) is defined, for every u∈[t,T], by
or, more explicitly,
Let us observe that there is a lot of flexibility in the choice of the adjustment processes Xk and corresponding processes αk. However, we will always assume that these processes are specified such that the above arguments of interpreting the actual ownership of the capital and thus also of the wealth process \(V(x,p,\phi, A,\mathcal {X})\) hold true.
As an immediate consequence of Definitions 1 and 4, it follows that the wealth process V of any self-financing trading strategy \((x_{t}, p_{t},\phi ^{t},\mathcal {C}^{t})\) admits the dynamics, for u∈[t,T],
One could argue that it would be possible to take Eqs. (10) and (11) as the definition of a self-financing trading strategy and subsequently deduce that equality (3) holds for the portfolio’s value \(V^{p}(x,p,\phi,\mathcal {C})\), which is then given by (9). We contend this alternative approach would not be optimal, since conditions in Definition 1 are obtained through a straightforward analysis of the trading mechanism and physical cash flows, whereas the financial justification of Eqs. (10)–(11) is less appealing.
Clearly, the wealth processes of a self-financing trading strategy is characterized in terms of two Eqs. 10 and (11). Observe that, using (10), it is possible to eliminate one of the processes ψj,l or ψj,b from (11) and thus to characterize the wealth process in terms of a single equation. One obtains in that way a (typically nonlinear) BSDE, which can be used to formulate various valuation problems for a given contract.
2.6 Trading in risky assets
Note that we do not postulate that the processes \(S^{i},\, i=1,2, \dots, d\) are positive, unless it is explicitly stated that the process Si models the price of a stock. Hence by the long cash position (resp. short cash position), we mean the situation when \(\xi ^{i}_{t} S^{i}_{t} \leq 0 \left (\text {resp}.\ \xi ^{i}_{t} S^{i}_{t} \geq 0\right)\), where \(\xi ^{i}_{t}\) is the number of hedger’s positions in the risky asset Si at time t.
2.6.1 Cash market trading
For simplicity of presentation, we assume that \(S^{i}_{t} \geq 0\) for all t∈[0,T]. Assume first that the purchase of \(\xi ^{i}_{t} > 0\) shares of the ith risky asset is funded using cash. Then, we set \(\psi ^{i,b}_{t}=0\) for all t∈[0,T] and thus the process Bi,b becomes irrelevant. Let us now consider the case when \(\xi ^{i}_{t} <0\). If we assume that the proceeds from short selling of the risky asset Si can be used by the hedger (this is typically not true in practice), we also set \(\psi ^{i,l}_{t}=0\) for all t∈[0,T], and thus the process Bi,l becomes irrelevant as well. Hence, under these stylized cash trading conventions, there is no need to introduce the funding accounts Bi,l and Bi,b for the ith risky asset. Since dividends Di are passed over to the lender of the asset, they do not appear in the term representing the gains/losses from the short position in the risky asset. In the simplest case of no market frictions and trading adjustments, and with the single risky asset S1, under the present short selling convention, (3) becomes
More practical short selling conventions for risky assets are discussed in the foregoing subsections.
2.6.2 Short selling of risky assets
Let us now consider the classical way of short selling of a risky asset borrowed from a broker. In that case, the hedger does not receive the proceeds from the sale of the borrowed shares of a risky asset, which are held instead by the broker as the cash collateral. The hedger may also be requested to post additional cash collateral to the broker and, in some cases, he may be paid interest on his margin account with the broker.Footnote 1 To represent these trading arrangements for the ith risky asset, we set \(\psi ^{i,l}_{t}=0\), \(\alpha ^{i}_{t}=\alpha _{t}^{i+d}=0\) and
where \(\beta ^{i}_{t}\) specifies the interest (if any) on the hedger’s margin account with the broker, \(\delta ^{i}_{t} \geq 0\) represents an additional cash collateral, and βi+d specifies the interest rate paid by the hedger for financing the additional collateral. Let us assume, for instance, that there is only one risky asset, S1, which is either sold short or purchased using cash as in Section 2.6.1. Then we obtain the following expression for the portfolio value
whereas Eq. 3 becomes
In particular, if there is no specific interest rate for remuneration of an additional collateral, then we set X2=0 and thus the last term in (13) should be omitted. It is worth noting that (12) can be seen as a special case of the following extended version of (2)
with d=1 and h1(x)=x+ for \(x \in \mathbb {R}\).
2.6.3 Repo market trading
Let us first consider the cash-driven repo transaction, the situation when shares of the ith risky asset owned by the hedger are used as collateral to raise cash.Footnote 2 To represent this transaction, we set
where Bi,b specifies the interest paid to the lender by the hedger who borrows cash and pledges the risky asset Si as collateral, and the constant hi,b represents the haircut for the ith asset pledged.
A synthetic short-selling of the risky asset Si using the repo market is obtained through the security-driven repo transaction, that is, when shares of the risky asset are posted as collateral by the borrower of cash and they are immediately sold by the hedger who lends the cash. Formally, this situation corresponds to the equality
where Bi,l specifies the interest amount paid to the hedger by the borrower of the cash amount \(\left (1-h^{i,l}\right)\left (\xi ^{i}_{t}\right)^{-} S^{i}_{t}\) and hi,l is the corresponding haircut.
If only one risky asset is traded and transactions are exclusively in repo market, then we obtain
In practice, it is reasonable to assume that the long and short repo rates for a given risky asset are identical, that is, Bi=Bi,l=Bi,b. In that case, we may and do set \(\psi ^{i}_{t} =(1-h^{i})\left (B^{i}_{t}\right)^{-1} \xi ^{i}_{t} S^{i}_{t} \), so that Eqs. 14 and (15) reduce to just one equation
According to this interpretation of Bi, equality (17) means that trading in the ith risky asset is done using the (symmetric) repo market and \(\xi ^{i}_{t}\) shares of a risky asset are pledged as collateral at time t, meaning that the collateralization rate equals 1. Under (17), Eq. 16 reduces to
2.7 Collateralization
We consider the situation when the hedger and the counterparty enter a contract and either receive or pledge collateral with value denoted by C, which is assumed to be a semimartingale. Generally speaking, the process C represents the value of the margin account. We let
where  and
and  By convention, the amount \(C^{+}_{t}\) is the cash value of collateral received at time t by the hedger from the counterparty, whereas \(C^{-}_{t}\) represents the cash value of the collateral pledged by him and thus transferred to his counterparty. For simplicity of presentation and consistently with the prevailing market practice, it is postulated throughout that only cash collateral may be delivered or received (for other collateral conventions, see, e.g., Bielecki and Rutkowski (2015)). According to ISDA Margin Survey 2014, about 75% of non-cleared OTC collateral agreements are settled in cash and about 15% in government securities. We also make the following natural assumption regarding the value of the margin account at the contract’s maturity date.
By convention, the amount \(C^{+}_{t}\) is the cash value of collateral received at time t by the hedger from the counterparty, whereas \(C^{-}_{t}\) represents the cash value of the collateral pledged by him and thus transferred to his counterparty. For simplicity of presentation and consistently with the prevailing market practice, it is postulated throughout that only cash collateral may be delivered or received (for other collateral conventions, see, e.g., Bielecki and Rutkowski (2015)). According to ISDA Margin Survey 2014, about 75% of non-cleared OTC collateral agreements are settled in cash and about 15% in government securities. We also make the following natural assumption regarding the value of the margin account at the contract’s maturity date.
Assumption 2
The \(\mathbb {G}\)-adapted collateral amount process C satisfies C T =0.
Typically this means that the collateral process C will have a jump at time T from CT− to 0. The postulated equality C T =0 is simply a convenient way of ensuring that any collateral amount posted is returned in full to the pledger when the contract matures, provided that default events have not occurred prior to or at maturity date T. As soon as the default events are also modeled, we will need to specify closeout payoffs (see Section 2.8.1).
Let us first make some comments from the hedger’s perspective regarding the crucial features of the margin account. The financial practice may require to hold the collateral amounts in segregated margin accounts, so that the hedger, when he is a collateral taker, cannot make use of the collateral amount for trading. Another collateral convention mostly encountered in practice is rehypothecation (around 90% of cash collateral of OTC contracts are rehypothecated), which refers to the situation where the hedger may use the collateral pledged by his counterparties as collateral for his contracts with other counterparties. Obviously, if the hedger is a collateral provider, then a particular convention regarding segregation or rehypothecation is immaterial for the dynamics of the value process of his portfolio. We refer the reader to Bielecki and Rutkowski (2015) and Crépey et al. (2014) for a detailed analysis of various conventions on collateral agreements. Here we will examine some basic aspects of collateralization (sometimes also called margining) in our context.
In general, the cash adjustments due to collateralization are
where the remuneration processes β1 and β2 determine the interest rates paid or received by the hedger on collateral amounts C+ and C−, respectively. The auxiliary processes α1 and α2 introduced in (20) are used to cover alternative conventions regarding rehypothecation and segregation of margin accounts. Note that we always set \(\alpha ^{2}_{t}=1\) for all t∈[0,T] when considering the portfolio of the hedger, since a particular convention regarding rehypothecation or segregation is manifestly irrelevant for the pledger of collateral.
2.7.1 Rehypothecated collateral
As it is customary in the existing literature, we assume that rehypothecation of cash collateral means that it can be used by the hedger for his trading purposes without any restrictions. To cover this stylized version of a rehypothecated collateral for the hedger, it suffices to set \(\alpha ^{1}_{t}=\alpha ^{2}_{t} =1\) for all t∈[0,T], so that for the hedger we obtain \(\alpha _{t}^{1}X^{1}_{t}+\alpha _{t}^{2}X^{2}_{t}=C_{t}\). Consequently, the cash adjustment corresponding to the margin account equals
2.7.2 Segregated collateral
Under segregation, the collateral received by the hedger is kept by the third party, so that it cannot be used by the hedger for his trading activities. In that case, we set \(\alpha ^{1}_{t}=0\) and \(\alpha ^{2}_{t} =1\) for all t∈[0,T] and thus \(\alpha _{t}^{1}X^{1}_{t}+\alpha _{t}^{2}X^{2}_{t}=-C^{-}_{t}\). Hence the corresponding cash adjustment term ϖ equals
2.7.3 Initial and variation margins
In market practice, the total collateral amount is usually represented by two components, which are termed the initial margin (also known as the independent amount) and the variation margin. In the context of self-financing trading strategies, this can be easily dealt with by introducing two (or more) collateral processes for a given contract A. It is worth mentioning that each of the collateral processes specified in the clauses of a contract is usually subject to a different convention regarding segregation and/or remuneration.
2.8 Counterparty credit risk
The counterparty credit risk in a financial contract arises from the possibility that at least one of the parties in the contract may default prior to or at the contract’s maturity, which may result in failure of this party to fulfil all their contractual obligations leading to financial loss suffered by either one of the two parties in the contract. We will model defaultability of the two parties to the contract in terms of their default times. We denote by τh and τc the default times of the hedger and his counterparty, respectively. We require that τh and τc are non-negative random variables defined on \((\Omega, \mathcal {G}, \mathbb {G}, \mathbb {P})\). If τh>T holds a.s. (resp. τc>T, a.s.) then the hedger (resp. the counterparty) is considered to be default-free in regard to the contract under study. Hence the counterparty risk is a relevant aspect for the contract maturing at T provided that \(\mathbb {P}(\tau \leq T)>0\) where τ:=τh∧τc is the moment of the first default.
From now on, we postulate that the process A models all promised (or nominal) cash flows of the contract, as seen from the perspective of the trading desk without accounting for the possibility of defaults of trading parties. In other words, A represents cash flows that would be realized in case none of the two parties has defaulted prior to or at the contract’s maturity. We will sometimes refer to A as to the counterparty risk-free cash flows and we will call the contract with cash flows A the counterparty risk-free contract. The key concept in the context of counterparty risk is the counterparty risky contract, which will be examined in the foregoing subsection.
2.8.1 Closeout payoff
Recall that τ denotes the moment of the first default. On the event \(\{ \tau <\infty \}\), we define the random variable Υ as
where Q is the Credit Support Annex (CSA) closeout valuation process of the contract A, ΔA τ =A τ −Aτ− is the jump of A at τ corresponding to a (possibly null) promised bullet dividend at τ, and C τ is the value of the collateral process C at time τ. In the financial interpretation, Υ+ is the amount the counterparty owes to the hedger at time τ, whereas Υ− is the amount the hedger owes to the counterparty at time τ. It accounts for the legal value Q τ of the contract, plus the bullet dividend ΔA τ to be received/paid at time τ, less the collateral amount C τ since it is already held by either the hedger (if C τ >0) or the counterparty (if C τ <0). We refer the reader to Section 3.1.3 in Crépey et al. (2014) for the detailed discussion of the specification of Υ.
One of the key financial aspects of the counterparty credit risk is the closeout payoff, which occurs if at least one of the parties defaults either before or at the maturity of the contract. It represents the cash flow exchanged between the two parties at the first-party-default time. The following definition of the closeout payoff, as usual given from the perspective of the hedger, is taken from Crépey et al. (2014). The random variables R c and R h taking values in [0,1] represent the recovery rates of the counterparty and the hedger, respectively.
Definition 5
The CSA closeout payoff\(\mathfrak {K}\) is defined as

The counterparty risky cumulative cash flows process A♯ is given by

Let us make some comments on the form of the closeout payoff \(\mathfrak {K}\). First, the term C τ is due to the fact that the legal title to the collateral amount comes into force only at the time of the first default. The three terms appearing after C τ in (24) correspond to the CSA convention that the cash flow at the first default from the perspective of the hedger should be equal to Q τ +ΔA τ . Let us consider, for instance, the event {τ c <τ h }. If Υ+>0, then we obtain
where the equality holds whenever R c =1. If Υ−>0, then we get
Finally, if Υ=0, then \(\mathfrak {K}=C_{\tau }=Q_{\tau }+ \Delta A_{\tau } \). Similar analysis can be done on the remaining two events in (24).
Remark 1
Of course, there is no counterparty credit risk present under the assumption that \(\mathbb {P}(\tau >T)=1\). Let us consider the case where \(\mathbb {P}(\tau >T) < 1\). We denote by \(P^{e}_{t}\) the counterparty risk-free ex-dividend price of the contract at time t. If we set R c =R h =1, then we obtain
Hence the counterparty credit risk is still present, despite the postulate of the full recovery, unless the legal value Q τ perfectly matches the counterparty risk-free ex-dividend price \(P^{e}_{\tau }\). Obviously, the counterparty credit risk vanishes when R c =R h =1 and \(Q_{\tau }= P^{e}_{\tau } \), since in that case the so-called exposure at default (see Section 3.2.3 in Crépey et al. (2014)) is null.
2.8.2 Counterparty credit risk decomposition
To effectively deal with the closeout payoff in our general framework, we now define the counterparty credit risk (CCR) cash flows, which are sometimes called CCR exposures. Note that the events \(\left \{ \tau =\tau ^{h} \right \}=\left \{ \tau ^{h} \leq \tau ^{c} \right \}\) and \(\left \{ \tau =\tau ^{c} \right \}=\left \{ \tau ^{c} \leq \tau ^{h} \right \}\) may overlap.
Definition 6
By the CCR processes, we mean the processes CL,CG and RP where the credit lossCL equals

the credit gain CG equals

and the replacement process is given by

The CCR cash flow is given by ACCR=CL+CG+CR.
It is worth noting that the CCR cash flows depend on the processes A,C and Q. The next proposition shows that we may interpret the counterparty risky contract as the basic contract A, which is complemented by the collateral adjustment process \(\mathcal {X}=\left (X^{1},X^{2}\right)= (C^{+},-C^{-})\) and the CCR cash flow ACCR. In view of this result, the counterparty risky contract \((A^{\sharp },\mathcal {X})\) admits the following formal decompositions \((A^{\sharp },\mathcal {X}) = (A,\mathcal {X})+(A^{\text {CCR}},0)\) and \((A^{\sharp },\mathcal {X})=(A,0)+(A^{\text {CCR}},\mathcal {X})\).
Proposition 1
The equality \(A^{\sharp }_{t}=A_{t}+A^{\text {CCR}}_{t}\) holds for all t∈[0,T].
Proof
We first note that

where we used (23) in the last equality. Therefore, from (25) we obtain

which is the desired equality in view of Definition 6. □
Proposition 1 shows that cash flows of the counterparty risky contract can be formally decomposed into the counterparty risk-free component \((A^{1},\mathcal {X}^{1})=(A,\mathcal {X})\) and the CCR component \((A^{2},\mathcal {X}^{2})=\left (A^{\text {CCR}},0\right)\). This additive decomposition of the contract’s cash flows may be employed in pricing of a counterparty risky contract. For instance, one could attempt to compute the price of the contract \((A^{\sharp },\mathcal {X})\) using the following tentative decomposition
It is unlikely that this procedure would result in an overall arbitrage-free valuation of the counterparty risky contract in a nonlinear framework since, as we argue in Section 6, the additivity of ex-dividend prices obtained by solving nonlinear BSDEs fails to hold, in general.
2.9 Local and global valuation problems
Market adjustments, which are represented in our framework by the process \(\mathcal {X}\), may in fact depend both on the cash flow process A and the trading strategy φ. By the same token, the trading strategy φ will typically depend on the trading adjustments. So, a feedback effect between φ and \(\mathcal {X}\) is potentially present in our trading universe and, of course, this feature should be properly accounted for in valuation and hedging. Furthermore, it is important to distinguish between the case where the above-mentioned dependence is only on the current composition of the hedging strategy and the current level of the wealth process and where the dependence extends to the history of these processes. If the contract \((A,\mathcal {X})\), the cash and funding accounts, and the prices of risky assets do not depend on the strict history (i.e., the history not including the current values of processes of interest) of a hedger’s trading strategy ϕ and its wealth process V(ϕ), then we say that the valuation problem is local. Otherwise, it is referred to as a global valuation problem. In view of (11), the distinction between local and global problems can be formalized through the following definition.
Definition 7
The valuation problem is local if \(X^{k}_{t}=v^{k}(t, V_{t}(\phi),\phi _{t})\) and \(d\beta _{t}^{k}=w^{k}(t,V_{t}(\phi),\phi _{t})\,dt\) for some \(\mathbb {G}\)-progressively measurable mappings \(v^{k},w^{k}:\Omega \times [0,T] \times \mathbb {R}^{3(d+1)} \to \mathbb {R} \) for every \(k=1,2,\dots,n\). The valuation problem is global if \(X^{k}_{t}=\bar {v}^{k}(t,V_{\cdot }(\phi),\phi _{\cdot })\) and \(d\beta _{t}^{k}= \bar {w}^{k}(t,V_{\cdot } (\phi),\phi _{\cdot })\,dt\) for some \(\mathbb {G}\)-non-anticipative functionals \(\bar {v}^{k},\bar {w}^{k} : \Omega \times [0,T] \times \mathcal {D} \left ([0,T], \mathbb {R}^{3(d+1)}\right) \to \mathbb {R} \) for every \(k=1,2,\dots,n\) where \( \mathcal {D} \left ([0,T], \mathbb {R}^{3(d+1)}\right)\) is the space of \(\mathbb {R}^{3(d+1)}\)-valued, \(\mathbb {G}\)-adapted, càdlàg processes on [0,T].
As one might guess, solutions to the two valuation problems will always coincide at time 0 but, in general, they may have very different properties at any date t∈(0,T). In particular, they will typically correspond to different classes of BSDEs: local problems correspond to classical BSDEs, whereas global ones can be dealt with through generalized BSDEs, which were introduced in the recent work by Cheridito and Nam (2017) (see also Zheng and Zong (2017)). It is important to stress that the distinction between the local and global problems is not related to the concept of path-independent contingent claims or the Markov property of the underlying model for primary risky assets. It is only due to the above-mentioned (either local or global) feedback effect between the hedger’s trading decisions and the market conditions inclusive of particular adjustments for the contract at hand.
Example 1 As a stylized example of a global valuation problem, let us consider a contract, which lasts for two months (for concreteness, assume that it is a simple combination of the put and the call on the stock S1 with maturities equal to one month and two months, respectively). The borrowing rate for the hedger is set to be 5% per annum, rising to 6% after one month if the hedger borrows any cash during the first month and it will stay at 5% if he does not. Similarly, the lending rate initially equals 3% per annum and drops to 2% if the hedger borrows any cash during the first month. It is intuitively clear that the valuation problem here is global, since its solution on [t,T] will depend on the strict history of trading. In contrast, if the trading model has possibly different, but fixed, borrowing and lending rates, then the valuation problem for any contract will be local, in the sense introduced above, of course, unless some other trading adjustments will depend on the strict history of trading.
For instance, if the only adjustment is the variable margin account determined by the hedger’s valuation and with a constant remuneration rate, then the hedger’s valuation problem is local. Note that the valuation problem described above can be inherently global even when the stock price is governed under the real-world probability measure by Markovian dynamics and the contract under study is a standard call or put option (or any other path-independent contingent claim).
More general instances of local and global valuation problems are presented in Section 6 where we examine a BSDE approach to the nonlinear markets. Let us mention that most valuation problems examined in the existing literature are local and thus they can be solved using existing results for classical BSDEs. In contrast, global valuation problems are much harder to analyze, since they require to use novel classes of BSDEs (see Cheridito and Nam (2017), Zheng and Zong (2017) and the references therein).
3 No-arbitrage properties of nonlinear markets
The analysis of the self-financing property of a trading strategy should be complemented by the study of some kind of no-arbitrage property for the adopted market model. Due to the nonlinearity of a market model with differential funding rates, the question how to properly define the no-arbitrage property is already a nontrivial matter, even when no additional portfolio constraints or trading adjustments are taken into account. Nevertheless, we will argue that it can be effectively dealt with using some reasonably general definition of an arbitrage opportunity associated with trading. Let us stress that we only examine here a nonlinear extension of the classical concept of an arbitrage opportunity and hence the simplest definition of no-arbitrage, sometimes abbreviated as NA (see, for instance, part (iv) in Definition 2.2 in Fontana (2015)), as opposed to much more sophisticated concepts, such as: NFLVR (no free lunch with vanishing risk), NUPBR (no unbounded profit with bounded risk, which is also known as the no-arbitrage of the first kind, that is, NA1) or NIP (no increasing profit). The introduction of more sophisticated no-arbitrage conditions is motivated by the desire to establish a suitable version of the fundamental theorem of asset pricing (FTAP), which shows the equivalence between a particular form of no-arbitrage and the existence of some kind of a “martingale measure” for the discounted prices of primary assets. Due to the complexity of a general nonlinear market model, it is unlikely that the martingale technique underpinning the FTAP in the linear setup will also prove useful when working within the general nonlinear framework (see, however, Pulido (2014) who established the FTAP for a very special, and hence tractable, case of a nonlinear market with short sales prohibitions). In this paper, we only propose alternative definitions of no-arbitrage in a nonlinear framework and we give sufficient conditions for the no-arbitrage property of a general nonlinear market model.
3.1 No-arbitrage pricing principles
Let us first describe very succinctly the classical valuation paradigm for financial derivatives. In essence, a general approach to the arbitrage-free pricing hinges, at least implicitly, on the following arguments:
Step (L.1). One first checks whether a market model with predetermined trading rules and primary traded assets is arbitrage-free, where the definition of an arbitrage opportunity is a mathematical formalization of the real-world concept of a risk-free profitable trading opportunity. In fact, depending on the framework at hand, several alternative definitions of “no-arbitrage” were studied (for an overview, see Fontana (2015)).
Step (L.2). Given a financial derivative for which the price is yet unspecified, one proposes a price (not necessarily unique) and checks whether the extended model (that is, the model where the financial derivative is postulated to be an additional traded asset) preserves the no-arbitrage property in the sense made precise in Step (L.1).
The valuation procedure outlined above can be referred to as the arbitrage-free pricing paradigm. In any linear market model (see the comments after Definition 2), one can show that the unique price given by replication (or the range of no-arbitrage prices obtained using the concept of superhedging strategies in the case of an incomplete market) is consistent with the arbitrage-free pricing paradigm (L.1)–(L.2), although to establish this property in a continuous-time framework, one needs also to introduce the concept of admissibility of a trading strategy. In particular, the strict comparison property of linear BSDEs can be employed to show that replication (or superhedging) will indeed yield prices for derivatives that are consistent with the arbitrage-free pricing paradigm.
Alternatively, a suitable version of the fundamental theorem of asset pricing can be used to show that the discounted prices defined through admissible trading strategies are σ-martingales (hence, in fact, supermartingales) under an equivalent local martingale measure. The latter property is a well known fundamental feature of stochastic integration, so it covers all linear market models. Obviously, our very brief summary of linear arbitrage-free pricing theory is rather superficial and we acknowledge that it should be complemented by suitable assumptions on prices of traded assets and specific definitions of no-arbitrage. For a survey of classical results regarding no-arbitrage properties of linear market models, we refer to the monograph by Delbaen and Schachermayer (2006) (see also papers by Karatzas and Kardaras (2007), Kardaras (2012), and Takaoka and Schweizer (2014) for more recent developments).
Let us now comment on the existing approaches to the nonlinear valuation of derivatives, as first developed by El Karoui and Quenez (1997) and El Karoui et al. (1997) and later applied by several authors to particular financial models or classes on contracts (see, for instance, Bichuch et al. (2018), Brigo and Pallavicini (2014), Crépey (2015a, b), Dumitrescu et al. (2017), Mercurio (2013) or Pallavicini et al. (2012a, b)). The most common approach to the valuation problem in a nonlinear framework seems to hinge, at least implicitly, on the following steps in which it is usually assumed that the hedger’s initial endowment is immaterial and thus it may be set to zero. In fact, Step (N.1) was explicitly addressed only in some of the above-mentioned works, whereas in most papers in the existing literature the authors were only concerned with the issue of finding a replicating or a superhedging strategy, as briefly outlined in Step (N.2). Also, to the best of our knowledge, the important issue emphasized in Step (N.3) has been completely ignored up to now, since apparently it was implicitly taken for granted that the cost of replication, as given by a solution to a suitable BSDE, is a fair price of the contract.
Step (N.1). The strict comparison argument for the BSDE associated with the wealth dynamics is used to show that one cannot construct an admissible trading strategy with the null initial wealth and the terminal wealth, which is non-negative almost surely and strictly positive with a positive probability (hence the classical no-arbitrage property holds).
Step (N.2). The price for a European contingent claim is defined using either the cost of replication or the minimal cost of superhedging. A suitable version of the strict comparison property for wealth processes can be used to show that, for some nonlinear market models, the two pricing approaches yield the same value for any replicable European claim.
Step (N.3). It remains to check if the tentative price, as given by the cost of replication or selected to be below the upper bound given by the minimal cost of superhedging, complies with some form of the no-arbitrage property of the extended market.
We will argue that the question whether the extended nonlinear market model preserves the no-arbitrage property (of course, according to each particular definition of no-arbitrage) is much harder to resolve than it was in the linear framework. Intuitively, this is due to the fact that trading in derivatives may essentially change the properties of the original nonlinear market, whereas some version of the FTAP can be used to give a positive answer to the same question in the linear setup. We propose a partial solution in the nonlinear framework by putting forward in Section 4.2 the concept of the regular market model (see Definitions 19 and 21) and we establish some results on the fair pricing in a regular model (see Propositions 3 and 5).
3.2 Discounted wealth and admissible strategies
To deal with the issue of no-arbitrage, we need to introduce the discounted wealth process and properly define the concept of admissibility of trading strategies. For any \(x \in \mathbb {R}\), we denote by \(\mathcal {B} (x)\) the strictly positive process given by, for all t∈[0,T],

Note that if B0,l=B0,b, then \({\mathcal {B}} (x)=B^{0}=B\). Furthermore, if x=0, then \(xB^{0,b}_{t}= xB^{0,l}_{t}=0\) for all t∈[0,T] and thus the choice of either B0,l or B0,b in the right-hand side of (26) will be in fact immaterial. It is natural to postulate that the initial endowment x≥0 (resp. x<0) has the future value \(x B^{0,l}_{t} \left (\text {resp}.\ xB^{0,b}_{t}\right)\) at time t∈[0,T] when invested in the cash account \(B^{0,l} \left (\text {resp}.\ B^{0,b}\right)\). We henceforth work under the following assumption.
Assumption 3
We postulate that:
-
(i)
for any initial endowment \(x \in \mathbb {R}\) of the hedger, the null contract\(\mathcal {N}=(0,0)\) belongs to
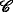 ,
, -
(ii)
for any \(x \in \mathbb {R}\), the trading strategy \(\left (x,0,\widehat {\phi },\mathcal {N} \right)\), where all components of \(\widehat {\phi }\) vanish except for either ψ0,l, if x≥0, or ψ0,b, if x<0, belongs to
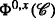 and \(V^{p}_{t} (x,0,\widehat {\phi }, \mathcal {N})=V_{t} (x,0,\widehat {\phi }, \mathcal {N})=x \mathcal {B}_{t}(x) \) for all t∈[0,T].
and \(V^{p}_{t} (x,0,\widehat {\phi }, \mathcal {N})=V_{t} (x,0,\widehat {\phi }, \mathcal {N})=x \mathcal {B}_{t}(x) \) for all t∈[0,T].
At the first glance, Assumption 3 may look trivial or even redundant but it should be made and it will be useful in the derivation of fundamental properties of fair prices. Condition (i) is indeed a rather obvious formal requirement. Note, however, that condition (ii) cannot be deduced directly from the self-financing condition, since it hinges on the additional postulate that there are no trading adjustments (such as: taxes, transactions costs, margin account, etc.) when the initial endowment is invested in the cash account. It is needed to show that the null contract has fair price zero at any date t∈[0,T]. Also, the trading strategy introduced in condition (ii) will serve as a natural benchmark for assessment of profits or losses incurred by the hedger. A natural extension of Assumption 3 to the case where we study trading strategies on [t,T] is also implicitly postulated without stating it explicitly.
In the next necessary step, we follow the standard approach of introducing the concept of admissibility for the discounted wealth. Towards this end, for any fixed t∈[0,T), we consider a hedger who starts trading at time t with the initial endowment x t and uses a self-financing trading strategy \((x_{t},p_{t},\phi ^{t},\mathcal {C}^{t})\), where the price \(p_{t} \in \mathcal {G}_{t}\) at which the contract \(\mathcal {C}^{t}\) is traded at time t is arbitrary. We also consider the strictly positive discounting process \(\mathcal {B}^{t} (x_{t})\), which is defined for all u∈[t,T] by

so that, in particular,  Then the wealth process discounted back to time t satisfies, for all u∈[t,T],
Then the wealth process discounted back to time t satisfies, for all u∈[t,T],
and we have the following natural concept of admissibility of a trading strategy on [t,T].
Definition 8
For any fixed t∈[0,T), we say that a trading strategy  is admissible if the discounted wealth \(\widetilde {V}_{u}\left (x_{t},p_{t},\phi ^{t},\mathcal {C}^{t}\right)\) is bounded from below by a constant. We denote by \( \Psi ^{t,x_{t}}(p_{t},\mathcal {C}^{t})\) the class of admissible strategies corresponding to \(\left (x_{t},p_{t},\phi ^{t},\mathcal {C}^{t}\right)\) and we denote by
is admissible if the discounted wealth \(\widetilde {V}_{u}\left (x_{t},p_{t},\phi ^{t},\mathcal {C}^{t}\right)\) is bounded from below by a constant. We denote by \( \Psi ^{t,x_{t}}(p_{t},\mathcal {C}^{t})\) the class of admissible strategies corresponding to \(\left (x_{t},p_{t},\phi ^{t},\mathcal {C}^{t}\right)\) and we denote by

the class of all admissible trading strategies on [t,T] relative to the class  of contracts for the hedger with the initial endowment x
t
at time t. In particular,
of contracts for the hedger with the initial endowment x
t
at time t. In particular,  is the class of all trading strategies that are admissible for the hedger with the initial endowment x at time t=0.
is the class of all trading strategies that are admissible for the hedger with the initial endowment x at time t=0.
3.3 No-arbitrage with respect to the null contract
A minimal no-arbitrage requirement for an underlying market model is that it should be arbitrage-free with respect to the null contract. Note that, consistently with Assumption 3 and the concept of replication (for the general formulation of replication of a non-null contract, see Definition 18), it is implicitly assumed in Definition 10 that the price at which the null contract is traded at time zero equals zero. Needless to say, this is a rather indisputable feature of any trading model.
Definition 9
Consider an underlying market model  An arbitrage opportunity with respect to the null contract (or a primary arbitrage opportunity) for the hedger with an initial endowment x is a strategy \((x,0,\varphi, \mathcal {N}) \in \Psi ^{0,x}(0, \mathcal {N})\) such that
An arbitrage opportunity with respect to the null contract (or a primary arbitrage opportunity) for the hedger with an initial endowment x is a strategy \((x,0,\varphi, \mathcal {N}) \in \Psi ^{0,x}(0, \mathcal {N})\) such that
Definition 10
If no primary arbitrage opportunity exists in the market model \(\mathcal {M}\) then we say that \(\mathcal {M}\) has the no-arbitrage property with respect to the null contract for the hedger with an initial endowment x.
For an arbitrary linear market model, Definition 10 reduces to the classical definition of an arbitrage opportunity. It is well known that the no-arbitrage property introduced in this definition is a sufficiently strong tool for the development of arbitrage-free pricing for financial derivatives in the linear framework. This does not mean, however, that Definition 10 is sufficiently strong to allow us to develop nonlinear arbitrage-free pricing theory, which would enjoy the properties desirable from either mathematical or financial perspective.
On the one hand, a natural definition of a hedger’s fair value (see Definition 15) is consistent with the concept of no-arbitrage with respect to the null contract and thus it seems to be theoretically sound. On the other hand, as we argue below, Definition 10 is manifestly not sufficient to ensure an efficient valuation and hedging approach in a general nonlinear market for the following reasons. First, it may occur that the replication cost of a contract does not satisfy the definition of a fair price, since the possibility of selling of a contract at the hedger’s replication cost may generate an arbitrage opportunity for him. An explicit example of a market model, which is arbitrage-free in the sense of Definition 10, but suffers from this deficiency, is analyzed in Section 4.2.3. Second, and more importantly, there are no well established methods of finding a fair price in a general nonlinear market that satisfies Definition 10.
We contend that the drawback of the definition of an arbitrage-free model with respect to the null contract is that it does not make an explicit reference to a class  of contracts under study. Indeed, it hinges on the specification of the class \(\Psi ^{0,x}(0, \mathcal {N})\) of trading strategies, but it makes no reference to the larger class
of contracts under study. Indeed, it hinges on the specification of the class \(\Psi ^{0,x}(0, \mathcal {N})\) of trading strategies, but it makes no reference to the larger class  To amend that drawback of Definition 10, it was proposed in Bielecki and Rutkowski (2015) to consider the concept of the no-arbitrage property for the trading desk with respect to a predetermined family
To amend that drawback of Definition 10, it was proposed in Bielecki and Rutkowski (2015) to consider the concept of the no-arbitrage property for the trading desk with respect to a predetermined family  of contracts.
of contracts.
3.4 No-arbitrage for the trading desk
Following Bielecki and Rutkowski (2015), we will now examine a stronger no-arbitrage property of a market model, which is intimately related to a predetermined family  of financial contracts. Our goal is here to propose a more stringent no-arbitrage condition, which not only accounts for the nonlinearity of the market, but also explicitly refers to a family of contracts under consideration. Regrettably, the class of models that are arbitrage-free in the sense of Definition 14 seems to be too encompassing and thus it is still unclear whether the valuation irregularities mentioned in the preceding section will be completely eliminated (for an example, see Section 4.2.3).
of financial contracts. Our goal is here to propose a more stringent no-arbitrage condition, which not only accounts for the nonlinearity of the market, but also explicitly refers to a family of contracts under consideration. Regrettably, the class of models that are arbitrage-free in the sense of Definition 14 seems to be too encompassing and thus it is still unclear whether the valuation irregularities mentioned in the preceding section will be completely eliminated (for an example, see Section 4.2.3).
For simplicity of notation, we consider here the case of t=0, but all definitions can easily be extended to the case of any date t. The symbols \(\mathcal {X}=\mathcal {X} (A)\) and \(\mathcal {Y}=\mathcal {Y} (- A)\) are used to emphasize that there is no reason to expect that the trading adjustments will satisfy the equality \(\mathcal {X} (-A)= -\mathcal {X} (A)\), in general. Therefore, we denote by \(\mathcal {Y}=\left (Y^{1}, \dots, Y^{n}; \alpha ^{1}(\mathcal {Y}), \ldots, \alpha ^{n}(\mathcal {Y}); \beta ^{1}(\mathcal {Y}), \ldots, \beta ^{n}(\mathcal {Y})\right)\) the trading adjustments associated with the cumulative cash flows process −A. In order to avoid confusion, we will use the full notation for the wealth process, for instance, \(V(x,p,\phi,\mathcal {C})=V(x,p,\phi, A,\mathcal {X})\), etc.
Remark 2
As already mentioned above, it is not necessarily true that the equality Yk=−Xk, holds for all k=1,2,…,n. For instance, this equality is satisfied by the variation margin, but it is not met by the initial margin and the regulatory capital, which are always non-negative.
Definition 11
For a contract \(\mathcal {C}=(A,\mathcal {X})\) and an initial endowment x, the combined wealth is defined as
where x1,x2 are arbitrary real numbers such that \(x=x_{1}+x_{2},\phi \in \Psi ^{0,x_{1}}(0,A,\mathcal {X}),\) and \(\, \bar \phi \in \Psi ^{0,x_{2}}(0,-A, \mathcal {Y})\). In particular, \({{V}^{\text {com}}_{0}}(x_{1}, x_{2},\phi, \bar \phi, A,\mathcal {X},\mathcal {Y})\,=\, x_{1} \!+x_{2}=x\).
The rationale for the term combined wealth is fairly transparent, since it comes directly from the financial interpretation of the process given by the right-hand side in (30). We argue below that it represents the aggregated wealth of the two traders, who are members of the same bank trading desk, and who are supposed to proceed as follows:
-
The first trader takes the long position in a contract \((A,\mathcal {X})\), whereas the second one takes the short position in the same contract, so that his position is formally represented by \((-A, \mathcal {Y})\). Since we assume that the long and short positions have exactly opposite prices, the corresponding cash flows p and −p coming to the trading desk (and not to individual traders) offset each other and thus the initial endowment x of the trading desk remains unchanged.
-
In addition, it is assumed that after the cash flows p and −p have already been netted, so they are no longer relevant, the initial endowment x is split into arbitrary amounts x1 and x2 meaning that x=x1+x2. Then each trader is allocated the respective amount x1 or x2 as his initial endowment and each of them undertakes active hedging of his respective position. It is now clear that the level of the initial price p at which the contract is traded at time zero is immaterial for both hedging strategies and the total (i.e., combined) wealth of the two traders is given by the right-hand side in (30).
Alternatively, the combined wealth may be used to describe the situation where a single trader takes long and short positions with two external counterparties and hedges them independently using his initial endowment x split into x1 and x2. Of course, in that case it is even more clear that the initial price p does not affect his trading strategies since the amount of cash received at time 0 from one of the counterparties is immediately transferred to the second one.
Remark 3
One can also observe that the following equality holds for any real number p
where \(\widetilde {x}_{1}=x_{1}-p\) and \(\widetilde {x}_{2}=x_{2}+p\) is another decomposition of x such that \(x=\widetilde {x}_{1}+\widetilde {x}_{2}\). However, Eq. (30) better reflects the actual trading arrangements and it has a clear advantage that a number p, which is not known a priori, does not appear in the expression for the combined wealth. Hence, (30) emphasizes the crucial feature that the combined wealth is independent of p. In fact, one can remark that the fact whether the trading desk is aware about the actual level of the price p is immaterial for the question whether an arbitrage opportunity for the trading desk exists in a particular market model.
Definition 12
A pair \((x_{1},\phi ; x_{2}, \bar \phi)\) of trading strategies introduced in Definition 11 is admissible for the trading desk if the discounted combined wealth process
is bounded from below by a constant. The class of strategies admissible for the trading desk is denoted by \(\Psi ^{0,x_{1},x_{2}}(A,\mathcal {X}, \mathcal {Y})\).
We are in a position to formalize the concept of an arbitrage-free model for the trading desk with respect to a particular family of contracts.
Definition 13
A pair \((x_{1},\phi ; x_{2},\bar \phi) \in \Psi ^{0,x_{1},x_{2}}(A,\mathcal {X}, \mathcal {Y})\) is an arbitrage opportunity for the trading desk with respect to a contract \((A,\mathcal {X})\) if the following conditions are satisfied
Definition 14
We say that the market model  has the no-arbitrage property for the trading desk if there are no arbitrage opportunities for the trading desk with respect to any contract \(\mathcal {C} \) from
has the no-arbitrage property for the trading desk if there are no arbitrage opportunities for the trading desk with respect to any contract \(\mathcal {C} \) from  .
.
Our main purpose in Sections 3.3 and 3.4 was to provide some simple and financially meaningful criteria that would allow us to detect and eliminate market models in which some particular form of arbitrage appears. Definition 10 and Definition 14 provide such criteria for accepting or rejecting any tentative nonlinear market model. It is easy to see that a model which is rejected according to Definition 14 will also be rejected if Definition 10 is applied. We do not claim, however, that these tentative tests are sufficient for an effective discrimination between acceptable and non-acceptable nonlinear models for valuation of derivatives. Therefore, in Definition 19, we will formulate additional conditions that should be satisfied by an acceptable model, which is then called a regular model.
3.5 Dynamics of the discounted wealth process
It is natural to ask whether the no-arbitrage for the trading desk can be checked for a given market model. Before we illustrate a simple verification method for this property, we need to introduce additional notation. Let us write
Lemma 2
The discounted combined wealth satisfies

where we set
Proof
For an arbitrary decomposition x=x1+x2, we write (note that the notation introduced in Eq. 28 is extended here, since x≠x i , in general)
From (10) and (11), using the Itô integration by parts formula, we obtain

and an analogous equality holds for \(\widetilde {V}(x_{2},p,\bar \varphi,-A,\mathcal {Y})\). Hence (32) follows from (30) and (31). □
We deduce from (34) that condition (ii) in Assumption 3 is satisfied, provided that no additional portfolio constraints are imposed (recall that condition (i) in Assumption 3 is always postulated to hold).
Assume now, in addition, that Bi,l=Bi,b=Bi for i=1,2,…,d. We define the processes Si,cld and \(\widehat {S}^{i,\text {cld}}\)
where in turn \(\widehat {S}^{i} := (B^{i})^{-1} S^{i}\). It is easy to check that
where \(\widetilde {B}^{i} (x) := (\mathcal {B}(x))^{-1} B^{i}\).
Corollary 1
Assume that Bi,l=Bi,b=Bi for i=1,2,…,d. Then the discounted combined wealth satisfies

Proof
It suffices to combine (32) with (35). □
3.6 Sufficient conditions for the trading desk no-arbitrage
The following result gives a sufficient condition for a market model to be arbitrage-free for the trading desk. The proof of Proposition 2 is pretty straightforward and thus it is omitted.
Proposition 2
Assume that there exists a probability measure \(\mathbb {Q}\), equivalent to \(\mathbb {P}\) on \((\Omega, \mathcal {G}_{T})\), and such that for any decomposition x=x1+x2 and any admissible combination of trading strategies \((x_{1},\phi,A, \mathcal {X})\) and \((x_{2}, \bar \phi, -A, \mathcal {Y})\) for any contract \((A,\mathcal {X})\) belonging to  the discounted combined wealth \({{\widetilde {V}}^{\text {com}}}(x_{1},x_{2},\phi, \bar \phi, A,\mathcal {X}, \mathcal {Y})\) is a supermartingale under \(\mathbb {Q}\). Then the market model
the discounted combined wealth \({{\widetilde {V}}^{\text {com}}}(x_{1},x_{2},\phi, \bar \phi, A,\mathcal {X}, \mathcal {Y})\) is a supermartingale under \(\mathbb {Q}\). Then the market model  is arbitrage-free for the trading desk.
is arbitrage-free for the trading desk.
Although Proposition 2 is fairly abstract, the sufficient condition formulated there can readily be verified, as soon as a specific market model is adopted (see, for instance, Bielecki and Rutkowski (2015) and Nie and Rutkowski (2015,2016a,2017 (published online on 18 April 2017)). To support this claim, we will examine an example of a market model with idiosyncratic funding for risky assets and rehypothecated cash collateral.
Example 2 We consider the special case where \(B^{0,l}=B^{0,b}=B=\mathcal {B} (x)\) and Bi,l=Bi,b=Bi for all i=1,2,…,d. If we temporarily assume that there are no additional portfolio constraints, then from (36) we obtain (for a special case of this formula, see Corollary 2.1 in Bielecki and Rutkowski (2015)
We postulate that the cash collateral is rehypothecated, so that n1=n=2 in Lemma 1. Then \(\alpha ^{1}_{t}=\alpha ^{2}_{t} =\alpha ^{1}_{t}(\mathcal {Y}) =\alpha ^{2}_{t}(\mathcal {Y})=1\) and \(X^{1}_{t}+Y^{1}_{t}=X^{2}_{t}+Y^{2}_{t}=0\) for all t∈[0,T]. Let us assume, in addition, that \(\xi _{t}^{i} S_{t}^{i}+ \psi _{t}^{i} B^{i}_{t}=\bar \xi _{t}^{i} S_{t}^{i}+\bar \psi _{t}^{i} B^{i}_{t} =0\) for all i and t∈[0,T], which means that the ith risky asset is fully funded using the repo account Bi (see Section 2.6.3). More generally, it suffices to assume that the following equalities are satisfied for all t∈[0,T]
Finally, let the remuneration processes satisfy \(\beta ^{k}(\mathcal {X}) =\beta ^{k}(\mathcal {Y})\) (the symmetry of collateral rates). Then the formula for the dynamics of the discounted combined wealth for the trading desk reduces to
and thus the model is arbitrage-free for the trading desk provided that there exists a probability measure \(\mathbb {Q}\), which is equivalent to \(\mathbb {P}\) on \((\Omega, \mathcal {G}_{T})\), and such that the processes \(\widehat {S}^{i,\text {cld}},\, i=1,2,\ldots, d\) are \(\mathbb {Q}\)-local martingales. This property is still a sufficient condition for the trading desk no-arbitrage when the cash account B0,l and B0,b differ, but the borrowing rate dominates the lending rate.
4 Hedger’s fair pricing and market regularity
We now address the issue of a fair pricing in the nonlinear framework under the assumption that the hedger has the initial endowment x t at time t. We assume that the model enjoys the no-arbitrage property either with respect to the null contract or for the trading desk and we consider the hedger who contemplates entering into the contract \(\mathcal {C}^{t} \) at time t. The first goal is to describe the range of the hedger’s fair prices for the contract \(\mathcal {C}^{t}\). Let \(p_{t} \in \mathcal {G}_{t}\) denote a generic price of a contract at time t, as seen from the perspective of the hedger. Hence if p t is positive, then the hedger receives at time t the cash amount p t from the counterparty, whereas a negative value of p t means that he agrees to pay the cash amount −p t to the counterparty at time t. In the next definition, we fix a date t∈[0,T) and we assume that the contract \(\mathcal {C}^{t}\) is traded at the price p t at time t. It is natural to ask whether in this situation the hedger can make a risk-free profit by entering into the contract and hedging it with an admissible trading strategy over [t,T]. We propose to call it a hedger’s pricing arbitrage opportunity. Recall that the arbitrage opportunities defined in Section 3 are related to the properties of a trading model, but they do not depend on the level of a price p t for \(\mathcal {C}^{t} \).
Definition 15
A trading strategy  is a hedger’s pricing arbitrage opportunity on [t,T] associated with the contract \(\mathcal {C}^{t} \) traded at p
t
at time t (or, briefly, a secondary arbitrage opportunity) if
is a hedger’s pricing arbitrage opportunity on [t,T] associated with the contract \(\mathcal {C}^{t} \) traded at p
t
at time t (or, briefly, a secondary arbitrage opportunity) if
and
It is clear that  is not a hedger’s pricing arbitrage opportunity on [t,T] if either
is not a hedger’s pricing arbitrage opportunity on [t,T] if either
or
We will refer to condition (41) as the hedger’s loss condition.
Definition 16
We say that \(p^{f}_{t}=p^{f}_{t}(x_{t},\mathcal {C}^{t})\) is a fair hedger’s price at time t for \(\mathcal {C}^{t}\) if there is no hedger’s secondary arbitrage opportunity  A fair hedger’s price \(p^{f}_{t}\) such that the loss condition holds for every trading strategy
A fair hedger’s price \(p^{f}_{t}\) such that the loss condition holds for every trading strategy  is called a loss-generating cost.
is called a loss-generating cost.
It is clear from Definitions 15 and 16 that if \(p^{f}_{t}\) is a fair price, then any trading strategy  necessarily satisfies either condition (40) or condition (41). Obviously, a fair hedger’s price depends both on the given endowment x
t
and the contract \(\mathcal {C}^{t}\) and thus the notation \(p^{f}_{t}(x_{t},\mathcal {C}^{t})\) is appropriate, but it will be frequently simplified to \(p^{f}_{t}\) when no danger of confusion may arise.
necessarily satisfies either condition (40) or condition (41). Obviously, a fair hedger’s price depends both on the given endowment x
t
and the contract \(\mathcal {C}^{t}\) and thus the notation \(p^{f}_{t}(x_{t},\mathcal {C}^{t})\) is appropriate, but it will be frequently simplified to \(p^{f}_{t}\) when no danger of confusion may arise.
A fair price prevents the hedger from making a sure profit with a positive probability and with no risk of suffering a loss. In contrast, it does not prevent the hedger from losing money, in general. It is thus natural to search for the highest level of a fair price. This idea motivates the following definition of the upper bound for the hedger’s fair prices \( \overline {p}^{f}_{t}(x_{t},\mathcal {C}^{t})=\mathrm {ess\,sup}\ \mathcal {H}^{f}_{t}(x_{t},\mathcal {C}^{t})\), where
We find it useful to study also the upper bound for the loss-generating costs, which is given by \( \overline {p}^{l}_{t}\left (x_{t},\mathcal {C}^{t}\right)=\mathrm {ess\,sup}\ \mathcal {H}^{l}_{t}\left (x_{t},\mathcal {C}^{t}\right)\), where
Definition 17
A trading strategy  is said to be the superhedging strategy for the contract \(\mathcal {C}^{t}\) if (38) holds, whereas the strict superhedging means that (38) and (39) are satisfied. If \(p^{s}_{t}=p^{s}_{t}\left (x_{t},\mathcal {C}^{t}\right)\) is such that there exists a superhedging strategy (resp. a strict superhedging strategy)
is said to be the superhedging strategy for the contract \(\mathcal {C}^{t}\) if (38) holds, whereas the strict superhedging means that (38) and (39) are satisfied. If \(p^{s}_{t}=p^{s}_{t}\left (x_{t},\mathcal {C}^{t}\right)\) is such that there exists a superhedging strategy (resp. a strict superhedging strategy)  then it is called a superhedging cost (resp. strict superhedging cost) at time t for \(\mathcal {C}^{t}\).
then it is called a superhedging cost (resp. strict superhedging cost) at time t for \(\mathcal {C}^{t}\).
The lower bound for the superhedging costs is given by \({\underline {p}}^{s}_{t} \left (x_{t},\mathcal {C}^{t}\right)={ess\,inf} \mathcal {H}^{s}_{t} (x_{t},\mathcal {C}^{t})\) where
and the lower bound for strict the superhedging costs equals \(\underline {p}^{a}_{t} \left (x_{t},\mathcal {C}^{t}\right)={ess\,inf} \mathcal {H}^{a}_{t} \left (x_{t},\mathcal {C}^{t}\right)\), where
From Definitions 16 and 17, it is obvious that \(\mathcal {H}^{l}_{t} \left (x_{t},\mathcal {C}^{t}\right) \subseteq \mathcal {H}^{f}_{t} \left (x_{t},\mathcal {C}^{t}\right)\) and \(\mathcal {H}^{a}_{t} \left (x_{t},\mathcal {C}^{t}\right) \subseteq \mathcal {H}^{s}_{t} \left (x_{t},\mathcal {C}^{t}\right)\). Moreover, the set \(\mathcal {H}^{f}_{t} \left (x_{t},\mathcal {C}^{t}\right)\) is the complement of \(\mathcal {H}^{a}_{t} \left (x_{t},\mathcal {C}^{t}\right)\) and the set \(\mathcal {H}^{l}_{t} \left (x_{t},\mathcal {C}^{t}\right)\) is the complement of \(\mathcal {H}^{s}_{t} \left (x_{t},\mathcal {C}^{t}\right)\) so that, obviously, we have that \(\mathcal {H}^{f}_{t} \left (x_{t},\mathcal {C}^{t}\right) \cap \mathcal {H}^{a}_{t} \left (x_{t},\mathcal {C}^{t}\right)=\emptyset \) and \(\mathcal {H}^{l}_{t} \left (x_{t},\mathcal {C}^{t}\right) \cap \mathcal {H}^{s}_{t} \left (x_{t},\mathcal {C}^{t}\right)=\emptyset \). Consequently, it is easy to see that
where, in principle, it may happen that \(\underline {p}^{s}_{0}(x,\mathcal {C})=- \infty \) or \({\overline {p}}^{f}_{0}(x,\mathcal {C})=\infty.\)
The next assumption looks fairly natural, but it is not necessarily satisfied by every nonlinear market model, so it should be checked on a case-by-case basis.
Assumption 4
For every  and t∈[0,T), all \(x_{t},p_{t},q_{t} \in \mathcal {G}_{t}\), and every trading strategy
and t∈[0,T), all \(x_{t},p_{t},q_{t} \in \mathcal {G}_{t}\), and every trading strategy  if q
t
≥p
t
on some event \(D \in \mathcal {G}_{t}\) such that \(\mathbb {P}(D)>0\), then there exists a trading strategy
if q
t
≥p
t
on some event \(D \in \mathcal {G}_{t}\) such that \(\mathbb {P}(D)>0\), then there exists a trading strategy  such that the inequality \(V_{T}\left (x_{t},q_{t},\psi ^{t},\mathcal {C}^{t}\right) \geq V_{T}\left (x_{t},p_{t},\phi ^{t},\mathcal {C}^{t}\right)\) holds on D.
such that the inequality \(V_{T}\left (x_{t},q_{t},\psi ^{t},\mathcal {C}^{t}\right) \geq V_{T}\left (x_{t},p_{t},\phi ^{t},\mathcal {C}^{t}\right)\) holds on D.
One may try to argue that if the hedger can enter into a contract at a higher price, then he can invest the cash difference q t −p t in the bank account till the contract’s maturity and trade according to the trading strategy φ corresponding to p t , and thus yielding a higher terminal wealth. However, this is not necessarily possible, since it may happen that φ requires borrowing from the bank account at some future times, while we postulated that simultaneous borrowing and lending of cash is prohibited in our model. More generally, selling at a higher price means essentially that the hedger starts with a different initial capital, which may change the trading strategy significantly. Formally, a simple combination of two self-financing strategies is no longer a self-financing strategy, in general. Furthermore, if we take into account the limited supply of investment grade assets (perhaps also inclusive of the bank account), then any strategy needs to satisfy suitable portfolio constraints, which could imply that the additional cash amount received by the hedger will necessarily be used to purchase assets with a much higher exposure to substantial losses. To sum up, due to the presence of portfolio constraints and trading adjustments, the monotonicity of the terminal wealth with respect to the price p t is by no means guaranteed, in general.
Assumption 4 is not explicitly stated in most existing papers devoted to the nonlinear valuation of derivatives. Note, however, that if the wealth process happens to be governed by some simple dynamics with no portfolio constraints or trading adjustments, then there is no need to postulate that this property holds, since it can be deduced from a suitable comparison theorem for ordinary differential equations. For a particular example of a model where Assumption 4 is satisfied, see Lemma 6.2 in the paper by (Dumitrescu et al. 2017) who postulate that the wealth process satisfies
where W is the Wiener process and M is the compensated martingale of the default indicator process. Let us stress that if the validity of Assumption 4 is not ensured, then one may only claim that the inequalities given in (46) are satisfied. In contrast, if Assumption 4 is met, then one obtains more informative conditions (47).
Under Assumption 4, it is easy to see that if \(p^{f}_{t}\) is a fair hedger’s price (resp. a loss-generating cost) at time t for \(\mathcal {C}^{t}\), then any \(p_{t} \in \mathcal {G}_{t}\) such that \(p_{t}\leq p^{f}_{t}\) is also a fair hedger’s price (resp. a loss-generating cost) at time t for that contract. Similarly, if a superhedging (resp. strict superhedging) strategy exists when \(\mathcal {C}^{t}\) is entered into at the price \(p^{s}_{t}\), then a superhedging (resp. strict superhedging) strategy exists as well for any p t satisfying \( p_{t} \geq p^{s}_{t}\). Therefore, if we postulate that Assumption 4 is met, then we have the following result in which we focus on the case where t=0, but it is easy to check that analogous properties are valid for any t∈(0,T) as well.
Lemma 3
Let Assumption 4 be satisfied. Then, for every contract  such that \(\underline {p}^{a}_{0}(x,\mathcal {C}) > - \infty \) and \({\overline {p}}^{f}_{0}(x,\mathcal {C}) < \infty \), we obtain the following intervals:
such that \(\underline {p}^{a}_{0}(x,\mathcal {C}) > - \infty \) and \({\overline {p}}^{f}_{0}(x,\mathcal {C}) < \infty \), we obtain the following intervals:
-
(i)
the interval \(I_{0}^{l}(x,\mathcal {C}):=\left (-\infty, \overline {p}^{l}_{0}(x,\mathcal {C})\right)\) of loss generating costs,
-
(ii)
the interval \(I_{0}^{r}(x,\mathcal {C}):=(\overline {p}^{l}_{0}(x,\mathcal {C}),\underline {p}^{a}_{0}(x,\mathcal {C}))=\big (\underline {p}^{s}_{0}(x,\mathcal {C}),{\overline {p}}^{f}_{0}(x,\mathcal {C})\big)\), where for every \(p \in I_{0}^{r}(x,\mathcal {C})\) there exists a trading strategy
 such that \(\mathbb {P}(\widetilde {V}_{T}(x, p,\phi,\mathcal {C})= x)=1\),
such that \(\mathbb {P}(\widetilde {V}_{T}(x, p,\phi,\mathcal {C})= x)=1\), -
(iii)
the interval \(I_{0}^{a}(x,\mathcal {C}):=\left (\underline {p}^{a}_{0}(x,\mathcal {C}), +\infty \right)\) of strict superhedging costs (arbitrage range),
where, in particular, the interval \(I_{0}^{r}(x,\mathcal {C})\) may be empty. Consequently,
Proof
Under Assumption 4, if \(p \in \mathcal {H}^{l}_{0}(x,\mathcal {C})\) (resp. \(p \in \mathcal {H}^{f}_{0}(x,\mathcal {C})\)) and q<p, then \(q \in \mathcal {H}^{l}_{0}(x,\mathcal {C})\) (resp. \(q \in \mathcal {H}^{f}_{0}(x,\mathcal {C})\)). Also, if \(p \in \mathcal {H}^{s}_{0}(x,\mathcal {C})\) (resp. \(p \in \mathcal {H}^{s}_{0}(x,\mathcal {C})\)) and q>p, then \(q\in \mathcal {H}^{s}_{0}(x,\mathcal {C})\) (resp. \(q \in \mathcal {H}^{a}_{0}(x,\mathcal {C})\)). It is now easy to see that the asserted properties are valid. □
Observe that nothing specific can be said about the end points of the three intervals introduced in Lemma 3, in general. Obviously, we have that either (a) \(I_{0}^{r}(x,\mathcal {C})=\emptyset \) and the equalities \(\overline {p}^{l}_{0}(x,\mathcal {C})={\overline {p}}^{f}_{0}(x,\mathcal {C})=\underline {p}^{s}_{0}(x,\mathcal {C})=\underline {p}^{a}_{0}(x,\mathcal {C})\) hold or (b) \(I_{0}^{r}(x,\mathcal {C})\ne \emptyset \) and thus \(\underline {p}^{s}_{0}(x,\mathcal {C})<{\overline {p}}^{f}_{0}(x,\mathcal {C})\). One may also consider the following stronger version of Assumption 4 under which case (b) cannot occur, by virtue of the postulated strict monotonicity of the terminal wealth with respect to the price p t .
Assumption 5
For every  and t∈[0,T), all \(x_{t}, p_{t}, q_{t} \in \mathcal {G}_{t}\), and every trading strategy
and t∈[0,T), all \(x_{t}, p_{t}, q_{t} \in \mathcal {G}_{t}\), and every trading strategy  if q
t
>p
t
on some event \(D \in \mathcal {G}_{t}\) such that \(\mathbb {P}(D)>0\), then there exists a trading strategy
if q
t
>p
t
on some event \(D \in \mathcal {G}_{t}\) such that \(\mathbb {P}(D)>0\), then there exists a trading strategy  such that the inequalities \(V_{T}(x_{t}, q_{t}, \psi ^{t},\mathcal {C}^{t}) \geq V_{T}\left (x_{t}, p_{t},\phi ^{t},\mathcal {C}^{t}\right)\) and \(V_{T}(x_{t}, q_{t}, \psi ^{t},\mathcal {C}^{t}) \ne V_{T}(x_{t},p_{t},\phi ^{t},\mathcal {C}^{t})\) are valid on D.
such that the inequalities \(V_{T}(x_{t}, q_{t}, \psi ^{t},\mathcal {C}^{t}) \geq V_{T}\left (x_{t}, p_{t},\phi ^{t},\mathcal {C}^{t}\right)\) and \(V_{T}(x_{t}, q_{t}, \psi ^{t},\mathcal {C}^{t}) \ne V_{T}(x_{t},p_{t},\phi ^{t},\mathcal {C}^{t})\) are valid on D.
It is clear that, under Assumption 5, the equality \(\underline {p}^{s}_{0}(x,\mathcal {C})=\underline {p}^{a}_{0}(x,\mathcal {C})\) holds and thus the following corollary to Lemma 3 is valid where, by convention, \(\inf \emptyset =\infty \) and \(\sup \emptyset =- \infty \).
Lemma 4
If Assumption 5 is satisfied, then for any contract  we have that
we have that
4.1 Replication on [0,T] and the gained value
Admittedly, the most commonly used technique for valuation of derivatives hinges on the concept of replication. In the present framework, it is given by the following definition, in which we consider the hedger with the initial endowment x at time 0 and where \(p^{r}_{0}\) stands for an arbitrary real number.
Definition 18
A trading strategy  is said to replicate the contract \(\mathcal {C} \) on [0,T] whenever \(V_{T}(x,p^{r}_{0},\phi,\mathcal {C})=x\mathcal {B}_{T}(x)\) or, equivalently, \(\widetilde {V}_{T}(x,p^{r}_{0},\phi,\mathcal {C})=x\). Then a real number \(p^{r}_{0}= p^{r}_{0}(x,\mathcal {C}) \) is said to be a hedger’s replication cost for \(\mathcal {C} \)at time 0 and the process \(p^{g} (x,\mathcal {C})\) given by
is said to replicate the contract \(\mathcal {C} \) on [0,T] whenever \(V_{T}(x,p^{r}_{0},\phi,\mathcal {C})=x\mathcal {B}_{T}(x)\) or, equivalently, \(\widetilde {V}_{T}(x,p^{r}_{0},\phi,\mathcal {C})=x\). Then a real number \(p^{r}_{0}= p^{r}_{0}(x,\mathcal {C}) \) is said to be a hedger’s replication cost for \(\mathcal {C} \)at time 0 and the process \(p^{g} (x,\mathcal {C})\) given by
is called the hedger’s gained value associated with the replicating strategy \((x,p^{r}_{0},\phi,\mathcal {C})\).
Note that the equality \(p^{g}_{0}(x,\mathcal {C})=p^{r}_{0}(x,\mathcal {C})\) is always satisfied since \(V_{0}(x,p^{r}_{0}(x,\mathcal {C}),\phi,\mathcal {C})= x+p^{r}_{0}(x,\mathcal {C})\). The financial interpretation of a hedger’s replication cost \(p^{r}_{0}(x,\mathcal {C}) \) for a given contract  is fairly straightforward. It represents either an increase or a reduction of the hedger’s initial endowment x, which is required to implement a trading strategy ensuring that the hedger’s wealth at time T, after the terminal payoff of the contract has been settled, perfectly matches the value at time T of the original initial endowment x invested in the cash account.
is fairly straightforward. It represents either an increase or a reduction of the hedger’s initial endowment x, which is required to implement a trading strategy ensuring that the hedger’s wealth at time T, after the terminal payoff of the contract has been settled, perfectly matches the value at time T of the original initial endowment x invested in the cash account.
As expected, for the null contract \(\mathcal {N} =(0,0)\), the self-financing strategy \((x,0,\phi, \mathcal {N})\), where the portfolio ϕ hinges on keeping all money in the bank account \(\mathcal {B}(x)\), is a replicating strategy for \(\mathcal {N}\) such that the gained value satisfies \(p^{g}_{t}(x, \mathcal {N})=0\) for all t∈[0,T]. The fact that the trading strategy \((x,0,\phi,\mathcal {N})\) is self-financing was postulated in Section 3.2 but, obviously, this assumption needs to be verified for each particular market model under study. Note also that the uniqueness of a replication cost \(p^{r}_{0}(x,\mathcal {C})\) is not ensured and, in fact, there is no reason to expect that it will always hold in every market model satisfying either Definition 10 or Definition 14 (for a counterexample, see Proposition 4).
Let us make some comments on replication costs. Suppose first that Assumption 4 is met. Let us assume that the interval \(I_{0}^{r}(x,\mathcal {C})\) introduced in part (ii) in Lemma 3 is nonempty. We already know that any number \(p \in \big (\overline {p}^{l}_{0}(x,\mathcal {C}), \underline {p}^{a}_{0}(x,\mathcal {C})\big)\) is necessarily a replication cost and a fair price for \(\mathcal {C}\) but it is unclear whether the minimal replication cost is well defined. In principle, it may also happen that there exists a replication cost either equal to, or strictly greater than, \(\underline {p}^{a}_{0}(x,\mathcal {C})\).
Let us now examine the case where the interval \(I_{0}^{r}(x,\mathcal {C})\) is empty. If the contract \(\mathcal {C}\) can be replicated, then it may then happen that \(\overline {p}^{l}_{0}(x,\mathcal {C})=\underline {p}^{a}_{0}(x,\mathcal {C})=p^{r}_{0}(x,\mathcal {C})\). It is not obvious, however, whether \(p^{r}_{0}(x,\mathcal {C})\) would be in that case a hedger’s fair price, since it may occur that a strict superhedging strategy with the same initial cost exists. Furthermore, it is also possible that \(\underline {p}^{a}_{0}(x,\mathcal {C}) < p^{r}_{0}(x,\mathcal {C})\) meaning that a strict superhedging may be in fact less expensive than replication. If the contract \(\mathcal {C}\) cannot be replicated, then it is not clear whether \(\overline {p}^{f}_{0}(x,\mathcal {C})\) is a fair price, although it coincides with the upper bound for loss-generating costs and with the lower bound for strict superhedging costs.
If Assumption 5 is met, then one can be a bit more specific. If the set of replication costs is nonempty, then only the lowest cost of replication can be a fair price (indeed, if p1 and p2 are two replication costs such that p1<p2, then p2 is also a strict superhedging cost and thus it is not a fair price). Consequently, if the set of all possible replication costs for a given contract is bounded from below then either (a) the lower bound for replication costs is not a replication cost and none of replication costs is a fair price or (b) the lower bound is a replication cost and it is a candidate for a maximal fair price for the contract.
To conclude, in a nonlinear market model, which is assumed to have the no-arbitrage property with respect to the null contract (or even the no-arbitrage property for the trading desk), a replication cost may fail to be a fair hedger’s price. To amend this shortcoming of a general nonlinear setup, we introduce in the next section a particular class of models in which replication yields a unique fair price for any contract \(\mathcal {C}\) belonging to a predetermined family  and such that a replicating strategy for \(\mathcal {C}\) exists.
and such that a replicating strategy for \(\mathcal {C}\) exists.
4.2 Market regularity on [0,T]
Once again, we consider the hedger with the initial endowment x at time 0. Intuitively, the concept of regularity with respect to a given family  of contracts is motivated by our desire to ensure that, for any contract from
of contracts is motivated by our desire to ensure that, for any contract from  , the cost of replication is never higher than the minimal cost of superhedging and, in addition, the cost of replication is a fair hedger’s price, in the sense of Definition 15.
, the cost of replication is never higher than the minimal cost of superhedging and, in addition, the cost of replication is a fair hedger’s price, in the sense of Definition 15.
Definition 19
We say that the market model  is regular on [0,T] with respect to
is regular on [0,T] with respect to  if Assumption 4 is met and for every replicable contract
if Assumption 4 is met and for every replicable contract  and for any replicating strategy \((x, p^{r}_{0}(x),\phi,\mathcal {X})\) the following properties hold:
and for any replicating strategy \((x, p^{r}_{0}(x),\phi,\mathcal {X})\) the following properties hold:
-
(i)
if p is such that there exists \((x,p,\phi,\mathcal {C}) \in \Psi ^{0,x}(p,\mathcal {C})\) satisfying
$$ \mathbb{P} \left(\widetilde{V}_{T}(x,p,\phi,\mathcal{C})\geq x \right)=1, $$(50)then \(p \geq p^{r}_{0}(x)\);
-
(ii)
if p is such that there exists \((x,p,\phi,\mathcal {C})\in \Psi ^{0,x} (p,\mathcal {C})\) such that
$$ \mathbb{P} \left(\widetilde{V}_{T}(x,p,\phi,\mathcal{C})\geq x \right)=1 $$(51)and
$$ \mathbb{P} \left(\widetilde{V}_{T}(x,p,\phi,\mathcal{C})>x \right) > 0, $$(52)then \(p > p^{r}_{0}(x)\).
By applying Definition 19 to the null contract \(\mathcal {N}=(0,0)\), we deduce that any regular market model is arbitrage-free for the hedger with respect to the null contract. It is not clear, however, whether an arbitrage opportunity for the trading desk may arise in a regular model.
Condition (i) in Definition 19 means that superhedging cannot be less expensive than replication, whereas condition (ii) postulates that any strict superhedging has a strictly higher cost than replication. It is important to observe that condition (i) implies that the replication cost \(p^{r}_{0}(x)\) for \(\mathcal {C} \) is unique. Moreover, if condition (i) holds, then condition (ii) is equivalent to the following condition
-
if p is such that there exists \((x,p,\phi,\mathcal {C})\in \Psi ^{0,x} (p,\mathcal {C})\) satisfying
$$ \mathbb{P} \left(\widetilde{V}_{T} (x,p,\phi,\mathcal{C}) \geq x \right)=1, $$(53)then the following implication is valid: if \(p=p^{r}_{0}(x)\), then
$$ \mathbb{P} \left(\widetilde{V}_{T} (x,p,\phi,\mathcal{C})=x \right)=1. $$(54)
Remark 4
In the special case of European claims with maturity T and no trading adjustments, conditions (i) and (ii) correspond to the comparison and strict comparison properties for solutions to BSDEs satisfied by the wealth process with different terminal conditions. In fact, the same idea underpins Definition 2.7 of the nonlinear pricing system introduced by El Karoui and Quenez (1997). Using similar arguments as El Karoui and Quenez (1997), we will show that the regularity of a market model can be established for a large variety of financial models using a BSDE approach.
4.2.1 Replicable contracts in regular markets
In this section, we focus on contracts that can be replicated. Proposition 3 shows that, in a regular market model, the cost of replication is the unique fair price of a contract  that can be replicated and the equalities \(p^{r}_{0}(x,\mathcal {C}) =\underline {p}^{a}_{0}(x,\mathcal {C})=\overline {p}^{l}_{0}(x,\mathcal {C})\) hold for such a contract. This means that the replication of a contract is indeed an effective method of valuation within the framework of a regular model, although this statement is not necessarily true when dealing with an arbitrary nonlinear market model.
that can be replicated and the equalities \(p^{r}_{0}(x,\mathcal {C}) =\underline {p}^{a}_{0}(x,\mathcal {C})=\overline {p}^{l}_{0}(x,\mathcal {C})\) hold for such a contract. This means that the replication of a contract is indeed an effective method of valuation within the framework of a regular model, although this statement is not necessarily true when dealing with an arbitrary nonlinear market model.
Proposition 3
Let a market model  be regular on [0,T] with respect to
be regular on [0,T] with respect to  . Then for every contract
. Then for every contract  that can be replicated on [0,T] we have:
that can be replicated on [0,T] we have:
-
(i)
the replication cost \(p^{r}_{0}(x,\mathcal {C})\) is unique,
-
(ii)
\(p^{r}_{0}(x,\mathcal {C})\) is the maximal fair price and the upper bound for loss-generating costs, that is, \(p^{r}_{0}(x,\mathcal {C})=\overline {p}^{f}_{0}(x,\mathcal {C})= \overline {p}^{l}_{0}(x,\mathcal {C})\),
-
(iii)
\(p^{r}_{0}(x,\mathcal {C})\) is the lower bound for superhedging costs and strict superhedging costs, that is, \(p^{r}_{0}(x,\mathcal {C})=\underline {p}^{s}_{0}(x,\mathcal {C})=\underline {p}^{a}_{0}(x,\mathcal {C})\).
Proof
As was mentioned, the uniqueness of the replication cost \(p^{r}_{0}(x,\mathcal {C})\) is an immediate consequence of condition (i) in Definition 19. Hence the interval \(I_{0}^{r}(x,\mathcal {C})\) defined in part (ii) in Lemma 3 is empty and thus, in particular, \(p^{r}_{0}(x,\mathcal {C}) \geq \overline {p}^{f}_{0}(x,\mathcal {C})\). Condition (ii) in Definition 19 implies that there is no trading strategy  such that conditions (51) and (52) are satisfied. This means that no hedger’s arbitrage opportunity arises (that is, no strict superhedging strategy for \(\mathcal {C} \) exists) if \(\mathcal {C} \) is traded at time 0 at its replication cost \(p^{r}_{0}(x,\mathcal {C})\) and thus we conclude that \(p^{r}_{0}(x,\mathcal {C})\) is the maximal fair price meaning that \(p^{r}_{0}(x,\mathcal {C})= \overline {p}^{f}_{0}(x,\mathcal {C})\). The remaining equalities are immediate consequences of Lemma 3. □
such that conditions (51) and (52) are satisfied. This means that no hedger’s arbitrage opportunity arises (that is, no strict superhedging strategy for \(\mathcal {C} \) exists) if \(\mathcal {C} \) is traded at time 0 at its replication cost \(p^{r}_{0}(x,\mathcal {C})\) and thus we conclude that \(p^{r}_{0}(x,\mathcal {C})\) is the maximal fair price meaning that \(p^{r}_{0}(x,\mathcal {C})= \overline {p}^{f}_{0}(x,\mathcal {C})\). The remaining equalities are immediate consequences of Lemma 3. □
4.2.2 Nonreplicable contracts
Let us make some comments on the properties of a contract \(\mathcal {C}\) for which replication in  is not feasible. If Assumption 4 is satisfied, then from Lemma 3 we obtain the following equalities \(\overline {p}^{l}_{0}(x,\mathcal {C})={\overline {p}}^{f}_{0}(x,\mathcal {C})=\underline {p}^{s}_{0}(x,\mathcal {C})=\underline {p}^{a}_{0}(x,\mathcal {C})\). Obviously, it would be interesting to know whether the common value is a fair price. Unfortunately, the definitive answer is not available, in general, since it may happen that it is indeed the maximal fair price, but it may also occur that it represents the cost of a strict superhedging strategy. Furthermore, it is not clear at all how to proceed to compute the value of \({\overline {p}}^{f}_{0}(x,\mathcal {C})\) (it would be perhaps enough to know this value since any strictly lower value is a loss-generating cost). Under either Assumption 5 or when we postulate that the market model \(\mathcal {M}\) is regular, we obtain the same conclusions as under Assumption 4 and thus they are not helpful when analyzing the valuation of nonreplicable contracts.
is not feasible. If Assumption 4 is satisfied, then from Lemma 3 we obtain the following equalities \(\overline {p}^{l}_{0}(x,\mathcal {C})={\overline {p}}^{f}_{0}(x,\mathcal {C})=\underline {p}^{s}_{0}(x,\mathcal {C})=\underline {p}^{a}_{0}(x,\mathcal {C})\). Obviously, it would be interesting to know whether the common value is a fair price. Unfortunately, the definitive answer is not available, in general, since it may happen that it is indeed the maximal fair price, but it may also occur that it represents the cost of a strict superhedging strategy. Furthermore, it is not clear at all how to proceed to compute the value of \({\overline {p}}^{f}_{0}(x,\mathcal {C})\) (it would be perhaps enough to know this value since any strictly lower value is a loss-generating cost). Under either Assumption 5 or when we postulate that the market model \(\mathcal {M}\) is regular, we obtain the same conclusions as under Assumption 4 and thus they are not helpful when analyzing the valuation of nonreplicable contracts.
4.2.3 Nonregular market model
Our next goal is to illustrate the issue of regularity of a model by providing a simple, albeit admittedly artificial, example of a model, which is not regular. We now assume that the hedger’s endowment at time 0 is null and we start by placing ourselves within the framework of Bergman (1995) model with differential borrowing and lending interest rates (see also Korn (1995), Nie and Rutkowski (2015) and Mercurio (2013). In particular, the stock price S1 is driven by the Black-Scholes dynamics and constant interest rates satisfy rb>rl. It is straightforward to verify that Bergman’s model  satisfies Definition 10 if, for instance, we take as
satisfies Definition 10 if, for instance, we take as  the class of long and short positions in all European put options written on the stock S1 and maturing at T. Moreover, the hedger is able to replicate, without borrowing any cash, the short position in the European put option on S1 with maturity T and any strike K>0. The hedger’s price of the European put in Bergman’s model is thus given by the classical Black-Scholes formula with the interest rate equal to rl and we henceforth denoted it as P
t
(K) for every t∈[0,T].
the class of long and short positions in all European put options written on the stock S1 and maturing at T. Moreover, the hedger is able to replicate, without borrowing any cash, the short position in the European put option on S1 with maturity T and any strike K>0. The hedger’s price of the European put in Bergman’s model is thus given by the classical Black-Scholes formula with the interest rate equal to rl and we henceforth denoted it as P
t
(K) for every t∈[0,T].
In the next step, we fix strike K>0 and the date U∈(0,T). For concreteness, we assume that T−U=1 and rl=0. In particular, the class  comprise only short and long positions in the put option with strike K. We complement the model \(\mathcal {M}_{B}\) by introducing an additional risky asset with the following price process with nondecreasing sample paths
comprise only short and long positions in the put option with strike K. We complement the model \(\mathcal {M}_{B}\) by introducing an additional risky asset with the following price process with nondecreasing sample paths

Since rl=0, we have that \(\mathbb {P} (2P_{U}(K)>K)>0\), due to the fact that 2P U (K)>K for S U sufficiently close to zero. It is obvious that \(S^{2}_{T}=1\) on the event {2P U (K)≤K}. On the other hand, on the event {2P U (K)>K}, we have
We henceforth assume that \(r^{b} > \ln 3\) in order to ensure that the interest rate rb dominates the rate of return on the asset S2. Obviously, the put option with strike K can be replicated in  (through the same strategy as in \(\mathcal {M}_{B}\), that is, using only Bl and S1 for trading) and thus its replication cost in \(\mathcal {M}\) is given by the Black-Scholes price P(K). We are ready to prove the following proposition describing the properties of \(\mathcal {M}\). It is easy to check that Assumption 4 (as well as Assumption 5) is satisfied by the model \(\mathcal {M}\).
(through the same strategy as in \(\mathcal {M}_{B}\), that is, using only Bl and S1 for trading) and thus its replication cost in \(\mathcal {M}\) is given by the Black-Scholes price P(K). We are ready to prove the following proposition describing the properties of \(\mathcal {M}\). It is easy to check that Assumption 4 (as well as Assumption 5) is satisfied by the model \(\mathcal {M}\).
Proposition 4
The market model  has the following properties:
has the following properties:
-
(i)
\(\mathcal {M}\) has the no-arbitrage property with respect to the null contract,
-
(ii)
\(\mathcal {M}\) has the no-arbitrage property for the trading desk,
-
(iii)
\(\mathcal {M}\) is nonregular and the extended model
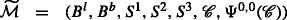 where S3=P(K) does not have the no-arbitrage property with respect to the null contract.
where S3=P(K) does not have the no-arbitrage property with respect to the null contract. -
(iv)
replication cost for the put option is not unique and the minimal cost of replication is given by the solution Y to the BSDE
$$ {dY}_{t}=\sum_{i=1}^{2} \xi_{t}^{i}\,dS^{i}_{t}, \quad Y_{T}=(K-S^{1}_{T})^{+}. $$(55)
Proof
Assertion (i) is easy to check. Intuitively, the increasing process S2 can be seen as an alternative (artificial) lending account to the constant lending account Bl=1 and thus, if the hedger has a surplus of cash, then he will invest it in the asset S2, rather than in the lending account Bl. It is thus enough to note that the model  satisfies Definition 10, as it can be seen as another instance of Bergman’s setup with a random lending rate.
satisfies Definition 10, as it can be seen as another instance of Bergman’s setup with a random lending rate.
For part (ii), we focus on the model  we focus on the model[JWFFXGRAPHICS] and we observe that Eq. 32 reduces to
we focus on the model[JWFFXGRAPHICS] and we observe that Eq. 32 reduces to
where A represents the put option, \(\widetilde {S}^{1}=S^{1} \big (\bar {B}^{l}\big)^{-1}\) and \(B^{0,b,l}=B^{b} \big (\bar {B}^{l}\big)^{-1}\). Since the process \(\widetilde {S}^{1}\) admits a martingale measure, the process B0,b,l is non-increasing and, by assumption, the processes ψ0,b and \(\bar \psi ^{0,b}\) are nonnegative, it is clear that no arbitrage opportunity for the trading desk may arise in the considered model, and thus also in \(\mathcal {M}\).
To prove (iii), we will show that the hedger who sells the put option at time 0 at its Black-Scholes price P0(K) can construct an arbitrage opportunity. To see this, assume that the hedger uses the replicating strategy for the put on the interval [0,U]. If the event {2P U (K)≤K} occurs, then he continues to replicate the put until its maturity date T. In contrast, if the event {2P U (K)>K} occurs, then he buys \(P_{U}(K)/S^{2}_{U}=P_{U}(K)\) of shares of the asset S2 and holds them till T. Then the hedger’s wealth at T, after delivery of the cash amount \((K-S^{1}_{T})^{+}\) to the buyer of the option, satisfies

Since \(\mathbb {P} (2P_{U}(K)> K)>0\) and it is clear that the wealth is always non-negative (so that the strategy is admissible), the strategy described above is an arbitrage opportunity for the hedger. Also, a strict superhedging strategy for the claim P T (K) can be obtained using the initial wealth equal to the replication cost. Indeed, using the premium P0(K), the hedger may either replicate ζ1:=P T (K) or strictly superhedge P T (K) by producing the terminal payoff

It is easy to check that ζ2≥ζ1 and \(\mathbb {P} (\zeta _{2} > \zeta _{1}) >0 \). We thus conclude that the model \(\mathcal {M}\) is nonregular and the extended model \(\widetilde {\mathcal {M}}\) does not satisfy Definition 10.
For the last assertion, we note that the put option can be replicated in the model  which is an extension of the Black-Scholes model in which the interest rate is random. This claim follows from the existence and uniqueness of a solution (Y,ϕ1,ϕ2) to BSDE (55) with Lipschitz continuous coefficients and the bounded terminal condition. Furthermore, the component ϕ2 of the replicating strategy is nonnegative and thus the same strategy replicates the option in \(\mathcal {M}\) and it is the least expensive replicating strategy in \(\mathcal {M}\). □
which is an extension of the Black-Scholes model in which the interest rate is random. This claim follows from the existence and uniqueness of a solution (Y,ϕ1,ϕ2) to BSDE (55) with Lipschitz continuous coefficients and the bounded terminal condition. Furthermore, the component ϕ2 of the replicating strategy is nonnegative and thus the same strategy replicates the option in \(\mathcal {M}\) and it is the least expensive replicating strategy in \(\mathcal {M}\). □
4.3 Replication and market regularity on [t,T]
The notion of the hedger’s gained value \(p^{g}_{t} (x,\mathcal {C}), \, t \in [0,T)\) reduces to the classical no-arbitrage price obtained through replication in the linear setup provided that the only cash flow of A after time 0 is the terminal payoff, which equals A T −AT−. Unfortunately, in a general nonlinear setup considered in this work, the financial interpretation of the hedger’s gained value at time t>0 is less transparent, since it depends on the hedger’s initial endowment, the past cash flows of a contract and the strategy implemented by the hedger on [0,t]. The following definition mimics Definition 18, but focuses on the restriction of a contract \(\mathcal {C} \) to the interval [t,T]. Note that here the discounted wealth process is given by Eq. (28). It is assumed in this section that \(\mathcal {C}^{t}\) can be replicated on [t,T) at some initial cost \(p^{r}_{t}\) at time t, in the sense of the following definition.
Definition 20
For a fixed t∈[0,T], let \(p^{r}_{t}\) be a \({\mathcal {G}}_{t}\)-measurable random variable. If there exists a trading strategy  such that
such that
then \(p^{r}_{t}=p^{r}_{t} \left (x_{t},\mathcal {C}^{t}\right)\) is called a replication cost at time t for the contract \(\mathcal {C}^{t}\) relative to the hedger’s endowment x t at time t.
As expected, Definition 19, and thus also Proposition 3, can be extended to any date t∈[0,T).
Definition 21
We say that a market model  is regular on [t,T] with respect to
is regular on [t,T] with respect to  if Assumption 4 is met and the following properties hold for every contract
if Assumption 4 is met and the following properties hold for every contract  that can be replicated:
that can be replicated:
-
(i)
if \(p_{t} \in \mathcal {G}_{t}\) and there exists
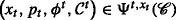 satisfying
$$ \mathbb{P} \left(\widetilde{V}_{T}(x_{t},p_{t},\phi^{t},\mathcal{C}^{t}) \geq x_{t}\right)=1, $$(57)
satisfying
$$ \mathbb{P} \left(\widetilde{V}_{T}(x_{t},p_{t},\phi^{t},\mathcal{C}^{t}) \geq x_{t}\right)=1, $$(57)then \(p_{t} \geq p^{r}_{t} \left (x_{t},\mathcal {C}^{t}\right)\);
-
(ii)
if \(p_{t} \in \mathcal {G}_{t} \) and there exists
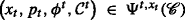 such that for some \(D \in \mathcal {G}_{t}\)
such that for some \(D \in \mathcal {G}_{t}\)
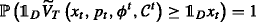 (58)
(58)and
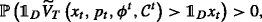 (59)
(59)then
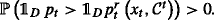
Similarly as for t=0, if condition (i) holds, then condition (ii) is equivalent to the following condition:
-
if \(p_{t} \in \mathcal {G}_{t} \) and there exists
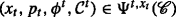 such that for some event \(D \in \mathcal {G}_{t}\)
such that for some event \(D \in \mathcal {G}_{t}\)
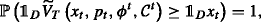 (60)
(60)then the following implication holds: if
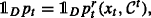 then
then
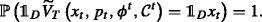 (61)
(61)
In the following extension of Proposition 3, we assume that the hedger’s endowment x t at time t is given and the contract \(\mathcal {C}\) has all cash flows on (t,T] so that \(\mathcal {C}^{t}=\mathcal {C}\). We now search for the hedger’s fair price for \(\mathcal {C}\) at time t assuming that a replication strategy exists. A closely related, but not identical, valuation problem is studied in Section 5.1 where we study the valuation at time t of a contract originated at time 0.
Proposition 5
Let a market model  be regular on [t,T] with respect to the class
be regular on [t,T] with respect to the class  . Then for every contract
. Then for every contract  such that \(\mathcal {C}=\mathcal {C}^{t}\) and which can be replicated on [t,T], we have:
such that \(\mathcal {C}=\mathcal {C}^{t}\) and which can be replicated on [t,T], we have:
-
(i)
the replication cost \(p^{r}_{t}(x_{t},\mathcal {C})\) is unique,
-
(ii)
\(p^{r}_{t}(x_{t},\mathcal {C})\) is the maximal fair price and the upper bound for loss-generating costs, that is, \(p^{r}_{t}(x_{t},\mathcal {C})=\overline {p}^{f}_{t}(x_{t},\mathcal {C})= \overline {p}^{l}_{t}(x_{t},\mathcal {C})\),
-
(iii)
\(p^{r}_{t}(x_{t},\mathcal {C})\) is the lower bound for superhedging costs and strict superhedging costs, that is, \(p^{r}_{t} (x_{t},\mathcal {C})=\underline {p}^{s}_{t}(x_{t},\mathcal {C}) =\underline {p}^{a}_{t}(x_{t},\mathcal {C})\).
The proof of Proposition 5 is very similar to the proof of Proposition 3 and thus it is omitted. According to Proposition 5, in any market model regular on [t,T], a replication cost is unique and it is the maximal fair price at time t for the hedger with the endowment x t at time t.
5 Pricing by replication in regular markets
In this section, it is assumed that a market model \(\mathcal {M}\) is regular. Our goal is to examine the properties of various kinds of prices for a contract \(\mathcal {C} \) under the assumption that it can be replicated on [t,T] for every t∈[0,T). Recall that for any fixed t∈[0,T) we denote by \((x_{t}, p_{t},\phi ^{t},\mathcal {C}^{t})\) a hedger’s trading strategy starting at time t with a \(\mathcal {G}_{t}\)-measurable endowment x t when a contract \(\mathcal {C}^{t}\) is traded at a \(\mathcal {G}_{t}\)-measurable price p t . For simplicity, we focus on contracts \(\mathcal {C}=(A,\mathcal {X})\) with a constant maturity date T, which correspond to non-defaultable contracts of European style. To deal with the counterparty credit risk, it suffices to replace A with the process A♯ introduced in Section 2.8.1 and a fixed maturity T with the effective maturity of a contract at hand (for instance, by T∧τ where τ is the random time of the first default or, more generally, by the effective settlement date of a contract in the presence of the gap risk). Furthermore, in the case of contracts of an American style or game options, the effective settlement date is also affected by respective decisions of both parties to prematurely terminate the contract.
5.1 Hedger’s ex-dividend price at time t
Since it was postulated that the initial endowment of the hedger at time 0 equals x, it is clear that any application of Definition 20 should be complemented by a financial interpretation of the hedger’s endowment x t at time t and a relationship between the quantity x t and the hedger’s initial endowment x should be clarified. One may consider several alternative specifications for x t , which correspond to different financial interpretations of valuation problems under study:
-
1.
A first natural choice is to set \(x_{t}=x_{t}(x):=x\mathcal {B}_{t}(x)\) meaning that the hedger has not been dynamically hedging the contract between time 0 and time t (this particular convention was adopted in Bielecki and Rutkowski (2015) and Nie and Rutkowski (2015,2016a). Then, the quantity \(p^{r}_{t}\left (x_{t},\mathcal {C}^{t}\right)\) is the future fair price at time t of the contract \(\mathcal {C}^{t}\), as seen at time 0 by the hedger with the endowment x at time 0, who decided to postpone trading in \(\mathcal {C}\) to time t. This specification of x t could be convenient if one wishes to study, for instance, the issue of valuation at time 0 of the option with the expiration date t written on the contract \(\mathcal {C}^{t}\).
-
2.
Alternatively, one may postulate that the contract was entered into by the hedger at time 0 at his replication cost \(p^{r}_{0}(x,\mathcal {C})\) and he decided to keep his position unhedged. In that case, the initial price, the cash flows, and the adjustments should be appropriately accounted for when computing the actual hedger’s endowment x t at time t using a particular market model.
-
3.
Next, one may assume that the contract was entered into by the hedger at time 0 at the price \(p^{r}_{0}(x,\mathcal {C})\) and was hedged by him on [0,t] through a replicating strategy ϕ, as given by Definition 18. Then the hedger’s endowment at time t>0 equals \(x_{t}=V_{t}(x,p^{r}_{0}(x,\mathcal {C}),\phi,\mathcal {C})\) and it is natural to expect that the equality \(p^{r}_{t}(x_{t},\mathcal {C}^{t})=0\) will hold for all t∈(0,T].
-
4.
Finally, one can simply postulate that the hedger’s endowment x t at time t is exogenously specified. Then Definition 20 reduces in fact to Definition 18 with essentially identical financial interpretation: we define the hedger’s initial price at time t for the contract \(\mathcal {C}^{t}\) given his initial endowment x t at time t. Of course, under this convention no relationship between the quantities x and x t exists.
In the next definition, we apply Definition 20 to the first of the above-mentioned specifications of x t , that is, we set \(x_{t}=x_{t}(x) := x \mathcal {B}_{t}(x)\). As in Definition 20, the discounted wealth is given by (28).
Definition 22
For a fixed t∈[0,T], assume that \(P^{e}_{t}\) is a \({\mathcal {G}}_{t}\)-measurable random variable. If there exists a trading strategy  such that
such that
then \(p^{e}_{t}\,=\,p^{e}_{t} (x,\mathcal {C}^{t})\) is called the hedger’s ex-dividend price at time t for the contract \(\mathcal {C}^{t} \).
Note that \(p^{r}_{0}(x,\mathcal {C})=p^{g}_{0}(x,\mathcal {C})=p^{e}_{0}(x,\mathcal {C})\) and \(p^{g}_{T} (x,\mathcal {C})=p^{e}_{T}\left (x,\mathcal {C}^{T}\right) =0\). The price given in Definition 22 is suitable when dealing with derivatives written on the contract \(\mathcal {C}^{t}\) as an underlying asset or, simply, when the hedger would like to compute the future fair price for \(\mathcal {C}^{t}\) without actually entering into the contract at time 0. Furthermore, it can also be used to define a proxy for the exit price of the contract \(\mathcal {C}^{t} \).
It is natural to ask whether the processes \(p^{g}_{t}(x,\mathcal {C})\) and \(p^{e}_{t}\left (x,\mathcal {C}^{t}\right)\) coincide for all t∈[0,T]. We will argue that the equality \(p^{g}_{t}(x,\mathcal {C})=p^{e}_{t}\left (x,\mathcal {C}^{t}\right)\) is valid for every t when the valuation problem is local, but it is not necessarily true for a global valuation problem (see Proposition 7). The reason is that in the former case the two processes satisfy identical BSDE, whereas in the latter case one obtains a generalized BSDE for the former process and a classical BSDE for the latter. It is also intuitively clear that in the case of the global valuation problem the two processes will typically differ, since the value of \(p^{e}_{t}\left (x,\mathcal {C}^{t}\right)\) is clearly independent of the hedger’s trading strategy on [0,t], as opposed to \(p^{g}_{t}(x,\mathcal {C})\), which may depend on the whole history of his trading. Since most valuation problems encountered in the existing literature have a local nature, to the best of our knowledge, this particular issue was not yet examined by other authors.
5.2 Exit price
The issue of valuation at time t is also important when we ask the following question: at which exit price a contract entered into by the hedger at time 0 can be unwound by him at time t. In theory, the easiest way to unwind at time t a contract originated at time 0 at the price \(p^{r}_{0}(x,\mathcal {C})=p^{g}_{0}(x,\mathcal {C})\) would be to transfer all obligations associated with the remaining part of the contract on [t,T] to another trader. Accordingly, the gained value \(p^{g}_{t} (x,\mathcal {C})\) for 0<t<T would be the amount of cash, which the hedger would be willing to pay to another trader who would then take the hedger’s position from time t onwards. This argument leads to the following definition of the hedger’s exit price.
Definition 23
The exit price for the contract \(\mathcal {C}\) entered into at time 0 by the hedger with the initial endowment x is given by the equality \(p^{m}_{t}(x,\mathcal {C}) := - p^{g}_{t}(x,\mathcal {C})\) for every t∈[0,T].
Definition 23 reflects the market practice where the exit price is related to the concept of unwinding the existing contract at time t at its current market value. Note, in particular, that the equality \(p^{g}_{t}(x,\mathcal {C})+p^{m}_{t}(x,\mathcal {C})= 0 \) holds for every t∈[0,T], meaning that the net value of the fully hedged position is null at any moment when the contract is marked to market. Unfortunately, a practical implementation of Definition 23 could prove difficult, especially when dealing with a global valuation problem, since it would require to keep track of past cash flows from the contract and gains from the hedging strategy (of course, provided the hedging strategy was implemented by the hedger). We thus contend that the proxy for the exit value \(p^{m}_{t} (x,\mathcal {C}) := - p^{e}_{t}(x,\mathcal {C})\) could be more suitable for most practical purposes when facing a global valuation problem. Since the equality \(p^{g}_{t}(x,\mathcal {C})=p^{e}_{t}(x,\mathcal {C})\) holds when the valuation problem is local, the issue of the choice of a marking to market convention is clearly immaterial in that case.
5.3 Offsetting price
Assume that the hedger is unable to transfer to another trader his existing position in the contract \(\mathcal {C} \) entered into at time 0. Then he may attempt to offset his future obligations associated with \(\mathcal {C}\) by taking the opposite position in an “equivalent” contract. In the next definition, we postulate that the hedger attempts to unwind his long position in \(\mathcal {C}=(A,\mathcal {X})\) at time t by entering into an offsetting contract\((-A^{t},\mathcal {Y}^{t})\). It is also assumed here that he liquidates at time t the replicating portfolio for \(\mathcal {C} \) so that his endowment at time t equals \(\widehat {V}_{t}(x,\mathcal {C}) := V_{t}(x,p^{r}_{0}(x,\mathcal {C}), \widehat {\phi },\mathcal {C})\), where \(\widehat {\phi }\) is a replicating strategy for \(\mathcal {C}\) on [0,T].
Definition 24
For a fixed t∈[0,T], let \(p^{o}_{t}\) be a \({\mathcal {G}}_{t}\)-measurable random variable. If there exists an admissible trading strategy \(\left (\widehat {V}_{t}(x,\mathcal {C}),p^{o}_{t},\phi ^{t},0,\mathcal {X}^{t}+\mathcal {Y}^{t}\right)\) on [t,T] such that
then \(p^{o}_{t}= p^{o}_{t}(x,\mathcal {C}^{t}) \) is called the offsetting price of \(\mathcal {C}^{t}=(A^{t},\mathcal {X}^{t})\) through \((-A^{t},\mathcal {Y}^{t})\) at time t.
Definition 24 takes into account the fact that the cash flows of At and −At (and perhaps also some cash flows associated with the corresponding adjustments \(\mathcal {X}^{t}\) and \(\mathcal {Y}^{t}\)) offset one another and thus only the residual cash flows need to be accounted for when computing the price at which the contract \(\mathcal {C} \) can be unwound by the hedger at time t.
In the special case where the equality \(\mathcal {X}^{t}+\mathcal {Y}^{t} =0\) holds for all t∈[0,T] (that is, the offsetting is perfect) we obtain the equality \(p^{o}_{t} (x,\mathcal {C}^{t})=- p^{g}_{t}(x,\mathcal {C})\) since then, in view of (49), we have that
where \(x \mathcal {B}_{t}(x)\) is the cash amount that is required to replicate the null contract (0,0) on [t,T].
6 A BSDE approach to nonlinear pricing
For each definition of the price, one may attempt to derive the corresponding backward stochastic differential equation (BSDE) by combining their definitions with dynamics (11) of the hedger’s wealth or, even more conveniently, with dynamics (34) of his discounted wealth. Subsequently, each particular valuation problem can be addressed by solving a suitable BSDE. In addition, one may use a BSDE approach to establish the regularity property of a market model at hand. To this end, one may either use the existing (strict) comparison theorems for solutions to BSDEs or, if needed, to establish original results. In this work, we are not analyzing these issues in detail since our goal is merely to derive BSDEs for the gained value and the ex-dividend price in a particular setup with trading adjustments and to emphasize the difference between local and global pricing problems. We conclude the paper by outlining important issues related to a BSDE approach to the counterparty credit risk.
6.1 BSDE for the gained value
We will first derive a generic BSDE associated with the hedger’s gained value \(p^{g}(x,\mathcal {C})\) introduced in Definition 18. For concreteness, we focus on the case of x≥0 so that the equality \(\mathcal {B}(x)=B^{l}\) is valid. To simplify the presentation, we also postulate that Bi,l=Bi,b=Bi for i=1,2,…,d and we consider trading strategies satisfying the funding constraint \(\widehat {\xi }^{i}_{t} S^{i}_{t}+\widehat {\psi }^{i}_{t} B^{i}_{t}=0\) for all \(i=1,2, \dots, d\) and every t∈[0,T]. Of course, the case where x<0 can be dealt with in an analogous manner. Recall that (see (33))
It is worth recalling that \(p^{r}_{0}(x,\mathcal {C})=p^{g}_{0}(x,\mathcal {C})\) (see Definition 18).
Lemma 5
Assume that a trading strategy  replicates a contract \(\mathcal {C}\). Then the processes \(\widehat {Y} := \widetilde {V}^{l} \left (x, p^{r}_{0}, \widehat {\phi },\mathcal {C}\right) :=\left (B^{0,l}\right)^{-1} V\left (x, p^{r}_{0}, \widehat {\phi },\mathcal {C}\right)\) and \(\widehat {Z}^{i} := \widetilde {B}^{i,l} \widehat {\xi }^{i}\) satisfy the BSDE
replicates a contract \(\mathcal {C}\). Then the processes \(\widehat {Y} := \widetilde {V}^{l} \left (x, p^{r}_{0}, \widehat {\phi },\mathcal {C}\right) :=\left (B^{0,l}\right)^{-1} V\left (x, p^{r}_{0}, \widehat {\phi },\mathcal {C}\right)\) and \(\widehat {Z}^{i} := \widetilde {B}^{i,l} \widehat {\xi }^{i}\) satisfy the BSDE
with the terminal condition \(\widehat {Y}_{T}=x\).
Proof
Under the present assumptions, (34) and (35) imply
where \(\widetilde {B}^{i,l} := \left (B^{0,l}\right)^{-1}B^{i},\, B^{0,b,l} := \left (B^{0,l}\right)^{-1}B^{0,b},\, \widetilde {\beta }^{k,l} := \left (B^{0,l}\right)^{-1} \beta ^{k} \). Eq. (10) and conditions \(\widehat {\psi }^{0,l} \geq 0, \widehat {\psi }^{0,b} \leq 0\) and \(\widehat {\psi }^{0,l} \widehat {\psi }^{0,b}=0\) yield
and
Note that the process \(\widehat {\psi }^{0,l}\) does not appear in (65) and the process \(\widehat {\psi }^{0,b}\) can also be eliminated from (65) by using (67). If we set \(\widehat {Y} := \widetilde {V}^{l} \left (x, p^{r}_{0}, \widehat {\phi },\mathcal {C}\right)\), then (65) can be represented as the BSDE
with the terminal condition \(\widehat {Y}_{T}=\widetilde {V}^{l}_{T}\left (x, p^{r}_{0}, \widehat {\phi },\mathcal {C}\right)=x\). In view of equality (35), BSDE (68) further simplifies to (64). □
In the next result, we focus on a market model satisfying regularity conditions introduced in Definition 21. From the regularity of a model, it follows that the hedger’s gained value \(p^{g}_{t}(x,\mathcal {C})\) is unique for each fixed t∈[0,T]. However, this does not suffice to define the process \(p^{g}(x,\mathcal {C})\) and thus in the next result we will make assumptions regarding the BSDE (64). First, we postulate that for a given x≥0 and any contract  there exists a unique solution \((\widehat {Y}, \widehat {Z})\) to (64) in a suitable space of stochastic processes. Second, we assume that the BSDE (64) enjoys the following variant of the strict comparison property.
there exists a unique solution \((\widehat {Y}, \widehat {Z})\) to (64) in a suitable space of stochastic processes. Second, we assume that the BSDE (64) enjoys the following variant of the strict comparison property.
Definition 25
The strict comparison property holds for the BSDE (64) if for any contract  and \(\left (\widehat {Y}^{2}, \widehat {Z}^{2}\right)\) are solutions with \(\mathcal {G}_{t}\)-measurable terminal conditions \(\xi ^{1}_{T} \geq \xi ^{2}_{T}\), respectively, then the equality
and \(\left (\widehat {Y}^{2}, \widehat {Z}^{2}\right)\) are solutions with \(\mathcal {G}_{t}\)-measurable terminal conditions \(\xi ^{1}_{T} \geq \xi ^{2}_{T}\), respectively, then the equality  for some t∈[0,T) and some \(D \in \mathcal {G}_{t}\) implies that
for some t∈[0,T) and some \(D \in \mathcal {G}_{t}\) implies that  .
.
It is also important to note that one needs to examine the manner in which the inputs in the BSDE (64) (that is, the stochastic processes introduced in Assumption 1) may possibly depend on the unknown processes \(\widehat {Y}\) and \(\widehat {Z}\).
According to Definition 7, the problem examined in this section will be an example of a local valuation problem if we postulate that Xk and βk satisfy \(X^{k}_{t}=v^{k}\left (t,\widehat {Y}_{t},\widehat {Z}_{t}\right)\) and \(d\beta _{t}^{k}= w^{k}\left (t,\widehat {Y}_{t},\widehat {Z}_{t}\right)\, dt\) for some \(\mathbb {G}\)-progressively measurable mappings \(v^{k},w^{k} : \Omega \times [0,T] \times \mathbb {R}^{d+1}\to \mathbb {R} \) for every \(k=1,2,\dots,n\). The same valuation problem becomes a global one if \(X^{k}_{t}=\bar {v}^{k}(t,\widehat {Y}_{\cdot },\widehat {Z}_{\cdot })\) and \(d\beta _{t}^{k}= \bar {w}^{k}\left (t,\widehat {Y}_{\cdot },\widehat {Z}_{\cdot }\right)\, dt\) for some \(\mathbb {G}\)-non-anticipative functionals \(\bar {v}^{k},\bar {w}^{k} : \Omega \times [0,T] \times \mathcal {D} \left ([0,T], \mathbb {R}^{d+1}\right) \to \mathbb {R} \) for every \(k=1,2,\dots,n\), where \(\mathcal {D} \left ([0,T],\mathbb {R}^{d+1}\right)\) is the space of \(\mathbb {R}^{d+1}\)-valued, \(\mathbb {G}\)-adapted, càdlàg processes on [0,T].
From Lemma 5, we deduce that a local valuation problem can be formulated in terms of a classical BSDE. In contrast, the situation where the inputs depend on the past history of the processes is harder to address, since a global valuation problem requires to study a generalized BSDE with non-anticipative functionals. Since both situations are covered by Proposition 6, we refer the reader to Cheridito and Nam (2017) and Zheng and Zong (2017) for the existence and uniqueness results for generalized BSDEs. It is worth noting that, to the best of our knowledge, so far no results on the strict comparison property for generalized BSDE are available. This should be contrasted with the theory of classical BSDEs where the strict comparison theorem plays an important role. In the next result, we suppose that the dynamics of the wealth process given by (65) and (67) are such that Assumption 4 is satisfied.
Proposition 6
Assume that the BSDE (64) has a unique solution \((\widehat {Y},\widehat {Z})\) for any contract  and the strict comparison property for solutions to (64) holds. Then, the following assertions are valid:
and the strict comparison property for solutions to (64) holds. Then, the following assertions are valid:
-
(i)
the market model is regular on [t,T] for every t∈[0,T];
-
(ii)
the hedger’s gained value satisfies \(p^{g}(x,\mathcal {C})= B^{0,l}\left (\widehat {Y} -x\right)\), where \(\left (\widehat {Y},\widehat {Z}\right)\) is a solution to BSDE (64) with the terminal condition \(\widehat {Y}_{T}=x\);
-
(iii)
the unique replicating strategy \(\widehat {\phi }\) for \(\mathcal {C} \) satisfies \(\widehat {\xi }^{i} =\left (\widetilde {B}^{i,l}\right)^{-1}\widehat {Z}^{i}\) and the cash components \(\widehat {\psi }^{0,l}\) and ψ0,b are given by (66) and (67), respectively, with \(V\left (x,p^{r}_{0},\widehat {\phi },\mathcal {C}\right)\) replaced by \(B^{0,l}\widehat {Y}\).
Proof
In view of Definition 21, it is clear that the existence, uniqueness and the strict comparison property for the BSDE (64) imply that the market model is regular on [t,T] for every t∈[0,T]. To establish (ii), we recall that the regularity of a model implies that the hedger’s gained value \(p^{g}_{t}(x,\mathcal {C})\) is unique. Moreover, we also know that \(p^{g}(x,\mathcal {C})\) satisfies for every t∈[0,T] (see (49))
which establishes the asserted equality \( p^{g}(x,\mathcal {C})=B^{0,l} (\widehat {Y}-x)\). In particular, the hedger’s replication cost \(p^{r}_{0}(x)\) satisfies \(p^{r}_{0}(x)=\widehat {Y}_{0}-x\) for any fixed initial endowment x≥0. Finally, part (iii) is an immediate consequence of Lemma 5. □
Of course, one needs to check for which models the assumptions of Proposition 6 are satisfied. For general results regarding BSDEs driven by one- or multi-dimensional continuous martingales, the reader is referred to Carbone et al. (2008), El Karoui and Huang (1997) and Nie and Rutkowski (2016b) and the references therein. Typically, a suitable variant of the Lipschitz continuity of a generator to a BSDE is sufficient to guarantee the desired properties of its solutions. Several instances of nonlinear market models with BSDEs satisfying the comparison property were studied by Nie and Rutkowski (2015,2016a,2018), although the concept of a regular model was not formally stated therein. In particular, they analyzed contracts with an endogenous collateral, meaning that an adjustment process Xk explicitly depends on a solution \(\widehat {Y}\) (or even on solutions to the valuation problems for the hedger and the counterparty).
Let us finally mention that since the model examined in this section is a special case of the model studied in Sections 3.5 and 3.6, it follows from Proposition 2 that to ensure that the model is arbitrage-free for the trading desk, it suffices to assume that there exists a probability measure \(\mathbb {Q}\), which is equivalent to \(\mathbb {P}\) on \((\Omega, \mathcal {G}_{T})\) and such that the processes \(\widehat {S}^{i,\text {cld}},\, i=1,2,\ldots, d\) given by (60) are \(\mathbb {Q}\)-local martingales. This assumption is also convenient if one wishes to prove the existence and uniqueness result for BSDE (64).
6.2 BSDE for the ex-dividend price
Our next goal is to derive the BSDE for the ex-dividend price \(p^{e}(x,\mathcal {C})\) introduced in Definition 22. As in Section 6.1, we work under the assumption that x≥0. Recall that, for a fixed t, the hedger’s ex-dividend price is implicitly given by the equality \(\widetilde {V}^{l}_{T}(x_{t}(x),p^{e}_{t},\phi ^{t},\mathcal {C}^{t})=x_{t}(x)\), where \(x_{t}(x)=x B^{l}_{t}\) and the discounting is done using the process \(\mathcal {B}^{t}_{\cdot }(x_{t}(x))\) given by (27). We henceforth assume that the valuation problem is local. This assumption is essential for validity of Lemma 6 and Proposition 7, so it cannot be relaxed.
Lemma 6
Assume that a trading strategy  replicates a contract \(\mathcal {C}^{t}\) on [t,T]. Then, the processes \(\bar Y_{u} := \widetilde {V}_{u}(x_{t}(x),p^{e}_{t},\phi ^{t},A^{t},\mathcal {X}^{t})\) and \(\bar Z^{i}_{u}:=\widetilde {B}^{i,l}_{u}(\xi ^{t}_{u})^{i}\), u∈[t,T], satisfy the following BSDE, for all u∈[t,T]
replicates a contract \(\mathcal {C}^{t}\) on [t,T]. Then, the processes \(\bar Y_{u} := \widetilde {V}_{u}(x_{t}(x),p^{e}_{t},\phi ^{t},A^{t},\mathcal {X}^{t})\) and \(\bar Z^{i}_{u}:=\widetilde {B}^{i,l}_{u}(\xi ^{t}_{u})^{i}\), u∈[t,T], satisfy the following BSDE, for all u∈[t,T]
with the terminal condition \(\bar Y_{T}=x\).
Proof
Arguing as in the proof of Lemma 5, we conclude that the dynamics of the discounted wealth \(\widetilde {V}_{u}(x_{t}(x),p^{e}_{t},\phi ^{t},A^{t},\mathcal {X}^{t})\) for u∈[t,T] are given by (65) and thus (69) is satisfied by \(\widehat {Y}\) and \(\widehat {Z}\) with the terminal condition \(\widetilde {Y}_{T}=x\). □
Although BSDEs (64) and (69) have the same shape, the features of their solutions heavily depend on a specification of the processes Xk and βk,l. The next result shows that the gained value and the ex-dividend price coincide when the valuation problem is local, so that the corresponding BSDEs are classical. In contrast, this property will typically fail to hold when a valuation problem is global, so that (64) becomes a generalized BSDE. In that case, Eq. (69) needs to be complemented by additional conditions regarding the processes Xk and βk,l.
Proposition 7
Under the assumptions of Proposition 6, if a valuation problem is local, then for any contract  the hedger’s gained value and the hedger’s ex-dividend price satisfy \(p^{e}_{t}(x,\mathcal {C})= p^{g}_{t}(x,\mathcal {C}^{t})\) for all t∈[0,T].
the hedger’s gained value and the hedger’s ex-dividend price satisfy \(p^{e}_{t}(x,\mathcal {C})= p^{g}_{t}(x,\mathcal {C}^{t})\) for all t∈[0,T].
Proof
On the one hand, under the postulate of uniqueness of solutions to BSDE (64) (and thus also to BSDE (69)), the equality \(\widehat {Y}_{t}=\bar Y_{t}\) is manifestly satisfied for all t∈[0,T]. On the other hand, from Definition 22, we obtain the equality \(x_{t}(x)+p^{e}_{t}(x,\mathcal {C}^{t})=B^{l}_{t} \bar Y_{t}\), which in turn yields \(p^{e}_{t}(x,\mathcal {C}^{t})= B^{l}_{t} \left (\bar Y_{t} - x\right)\). Since \(\widehat {Y}_{t}=\widetilde {Y}_{t}\), we conclude that the gained value \(p^{g}_{t}(x,\mathcal {C})=B^{l}_{t} \left (\widehat {Y}_{t} - x\right)\) and the ex-dividend price \(p^{e}_{t}(x,\mathcal {C}^{t})\) coincide for all t∈[0,T]. □
The property of a local valuation problem established in Proposition 7 is fairly general: its validity hinges on the existence and uniqueness of a solution to a common BSDE for the gained value and the ex-dividend price. This should be contrasted with the case of the global valuation problem where the equality \(p^{g}_{t}(x,\mathcal {C})=p^{e}_{t}(x,\mathcal {C}^{t})\) is always satisfied for t=0, but it is not likely to hold for any t>0.
6.3 BSDE for the CCR price
We now address the question raised in Section 2.8.2: can we disentangle the counterparty risk-free valuation of a credit risky contract from the CRR valuation? Although this is true in the linear setup where the price additivity is known to hold, the answer to this question is unlikely to be positive within a nonlinear framework. On the one hand, according to Proposition 1, the counterparty risky contract \((A^{\sharp },\mathcal {X})\) admits the following decomposition
where the first component is not subject to the counterparty credit risk (although it may include the margin account) and thus it is referred to as the counterparty risk-free contract, whereas the second component is concerned exclusively with the CCR (see Definition 6 for the specification of the CCR cash flow ACCR). On the other hand, however, in a nonlinear framework, the price of the full contract \((A^{\sharp },\mathcal {X})\) is unlikely to be equal to the sum of prices of its components appearing in the additive decomposition of the full contract.
To examine this problem more closely, let us assume that the underlying market model is sufficiently rich to allow for replication of the full contract \((A^{\sharp },\mathcal {X})\), as well as for replication of its two components \((A,\mathcal {X})\) and (ACCR,0). Of course, one can alternatively focus on the decomposition \((A^{\sharp },\mathcal {X})=(A,0)+(A^{\text {CCR}},\mathcal {X})\) in which the trading adjustments (in particular, the margin account) are assumed to affect the CCR part, rather than the counterparty risk-free contract (A,0). The choice of a decomposition should be motivated by practical considerations; one may argue that collateralization is nowadays a standard covenant in most contracts, not necessarily directly related to the actual level of exposure to the counterparty credit risk in a given contract.
If we denote by τh and τc the default times of the hedger and the counterparty, respectively, then τ=τh∧τc is the moment of the first default and thus the effective maturity of \((A^{\sharp },\mathcal {X})\) and (ACCR,0) is the random time \(\widehat {\tau }=\tau \wedge T\). For the counterparty risk-free contract \((A,\mathcal {X})\), it is convenient to formally assume that its maturity date equals T, since this component of the full contract is not exposed to the default risk.
By a minor extension of Lemma 5, we obtain the following BSDE for the full contract \((A^{\sharp },\mathcal {X})\)
with the terminal condition \(\widehat {Y}_{\widehat {\tau }}=x\). Let x=x1+x2 be an arbitrary split of the hedger’s endowment. Then we obtain the following BSDE corresponding to the counterparty risk-free contract \((A,\mathcal {X})\)
with \(\widehat {Y}^{1}_{T}=x_{1}\). The BSDE associated with the CRR component (ACCR,0) reads
with \(\widehat {Y}^{2}_{\widehat {\tau }}=x_{2}\). If the initial endowment x=0, then we may take x1 and x2 to be null as well.
The question formulated at the beginning of this section can be restated as follows: under which conditions the equality \(\widehat {Y}_{0}= \widehat {Y}^{1}_{0}+\widehat {Y}^{2}_{0}\) holds for solutions to BSDEs (71), (72) and (73), so that the three replication costs satisfy the following equality
which formally corresponds to decomposition (70) of the full contract and the split x=x1+x2 of the hedger’s initial endowment? Since this equality is unlikely to be satisfied (even when x=x1=x2=0, as it was implicitly assumed in most existing papers on the nonlinear approach to credit risk modeling), one could ask, more generally, whether the quantities \(\widehat {Y}_{0}\) and \(\widehat {Y}^{1}_{0}+\widehat {Y}^{2}_{0}\) are close to each other, so that some approximate equality is satisfied by the replication costs. Of course, an analogous question can also be formulated for the corresponding replicating strategies.
One needs first to address the issues of regularity and completeness of market models with default times. To this end, one may employ the existence and uniqueness results, as well as the strict comparison theorems, obtained for BSDEs with jumps generated by the occurrence of random times. BSDEs of this form are relatively uncommon in the existing literature on the theory of BSDEs, but they were studied in papers by Peng and Xu (2009) and Quenez and Sulem (2013). Of course, to be in a position to use results established in those papers, one would need to explicitly specify the price dynamics for non-defaultable risky assets \(S^{1}, \dots, S^{d-2}\) (usually, they are supposed to be driven by a multidimensional Brownian motion), as well as the manner in which default times (thus also the prices of defaultable assets Sd−1 and Sd) are defined. The latter issue is addressed in Peng and Xu (2009) or Quenez and Sulem (2013) through the so-called intensity-based approach, which was previously extensively studied in the credit risk literature. Furthermore, it would be convenient to assume that the cash and funding accounts, as well as remuneration processes, have absolutely continuous sample paths, so that BSDEs could be represented in the following generic form
where M1 and M2 are purely discontinuous \(\mathbb {G}\)-martingales associated with the price processes Sd−1 and Sd, respectively, and \(\bar A\) is a fixed process. Note that the generator g can be obtained from (71), (72) and (73) by straightforward computations.
From the financial perspective, to ensure the completeness of the market model at hand, one would need to postulate that some defaultable securities (typically, defaultable bonds issued by the two parties or credit default swaps) are among primary traded assets. Finally, it is necessary to explicitly specify the closeout valuation process Q (see Remark 1) and the collateral process C. When dealing with a local valuation problem, the most natural theoretical choice (albeit not necessarily easy to implement in practice) would be to set (see Proposition 7)
although the latter convention of the endogenous collateral is slightly cumbersome to handle, even when dealing with BSDEs driven by a multidimensional continuous martingale (see Nie and Rutkowski (2016b)). Note also that it would require to replace C τ by Cτ− when specifying the closeout payoff \(\mathfrak {K}\) (hence also the process A♯) in Section 2.8.1. For technical problems for BSDEs with jumps arising in this context and related to the classical immersion hypothesis and the way in which they can be resolved, the interested reader is referred to recent papers by Crépey and Song (2016,2017).
Within the framework of a linear model of credit risk, the issue of market completeness and various methods for replication were studied in several works (see, in particular, Bielecki et al. (2004,2006,2008). In contrast, only a few papers devoted to nonlinear models of credit risk are available. More recently, Crépey (2015a, b), Dumitrescu et al. (2017) and Bichuch et al. (2018) used BSDEs with jumps to solve the valuation and hedging problems for derivative contracts exposed to the counterparty credit risk. In Bichuch et al. (2018) and Dumitrescu et al. (2017), the authors focus on valuation of the full contract, whereas Crépey (2015a, b) examines the problem of the approximate additivity for the credit valuation adjustments.
7 Nonlinear valuation versus market practice
Although the goal of this paper is to formulate questions and give preliminary answers regarding the most fundamental issues pertinent to the theory of nonlinear arbitrage-free pricing, a few remarks concerning the current market practice and its relationship to theoretical results on nonlinear pricing could be appreciated by the reader. We also briefly describe some related recent papers where the issue of the so-called valuation adjustments was examined in both linear and nonlinear setups.
According to the prevailing practical approach, the full price for a counterparty risky contract is typically obtained by combining, at least implicitly, the so-called clean price of the basic contract (A,0) with various valuation adjustments. The clean price and the corresponding hedge are computed by the trading desk using the classical linear approach under a manifestly unrealistic, but obviously very convenient, assumption that a proxy for the unique risk-free rate is available for funding of all trading activities and the counterparty credit risk is ignored. It is thus clear that, from the theoretical point of view, the clean price can be computed as a solution to a linear BSDE, as in the classical arbitrage-free pricing theory. In contrast, various valuation adjustments are determined by the dedicated CVA desk in such a way that they account for all other features of a contract and trading conditions, such as: differential funding costs, the presence of the margin account, the counterparty credit risk, regulatory requirements, etc.. This means that, according to practical approach adopted by most banks, the full price of a new deal is implicitly represented as follows
where the clean price is given by a solution to a linear BSDE and the total valuation adjustment (denoted as XVA) is determined by solving either a linear or a nonlinear BSDE. Of course, if all three terms appearing in (74) (that is: the full price, the clean price, and the total valuation adjustment) are given by solutions to particular linear BSDEs, then it is possible to argue that decomposition (74) can be formally justified. However, if the valuation adjustment (and thus also the full price) is given by a solution to a nonlinear BSDE, which is the case of our primary interest, then the two terms appearing in the right-hand side in (74) cannot be computed separately and subsequently aggregated to obtain the full price. This observation is valid, in general, despite the fact that the clean price is always computed through a solution to linear BSDE or, equivalently, a suitable version of the risk-neutral valuation formula and thus it enjoys the additivity property across several (uncollateralized and non-defaultable) deals. Therefore, in our opinion, the introduction of the concept of the clean price, although convenient in practice since it refers to the pre-crisis experience and facilitates calibration of commonly used models for the underlying securities, may further complicate the theoretical problem of searching for the full price of a contract and the corresponding hedging strategy when working in a nonlinear setup.
Let us illustrate the issue of non-additivity by focusing on a specific nonlinear setup. We stress that by the non-additivity of pricing we mean here the property that the clean price and the total valuation adjustment cannot be computed separately by splitting the cash flows of a contract and perhaps even to use a different model to deal with each of components. Brigo et al. (2018) have recently shown that the risk-neutral valuation approach with adjusted cash flows based on a proxy for the risk-free interest rate, which was introduced and studied by Pallavicini et al. (2012a, b), can be formally supported using the replication-based approach in which a proxy for the risk-free interest rate can be chosen in a completely arbitrary way. Indeed, it is possible to use any \(\mathbb {G}\)-adapted and suitably integrable process α to play the role of a proxy for the risk-free interest rate, since the financial interpretation (if any) of this process is irrelevant for the derivation of decomposition (75). It was proven in Proposition 3.2 in Brigo et al. (2018), under the assumption of null initial endowment (so that x=x t (x)=0 for all t∈[0,T]), that the ex-dividend hedger’s price of an attainable collateralized contract \(\mathcal {C} = (A^{\sharp },C)\) equals, on the event {t<τ} for every t∈[0,T],

where we denote \(F_{t} =\psi ^{0,l}_{t} B^{0,l}_{t}+\psi ^{0,b}_{t} B^{0,b}_{t},\, F^{i}_{t} =\xi ^{i}_{t} S^{i}_{t}\), and

and where cl (resp. cb) is the remuneration rate for the cash collateral pledged (resp. received) by the hedger. Furthermore, \(p^{e,\alpha }_{t}(A)\) is the ex-dividend clean price and the probability measure \({\mathbb Q}^{\alpha }\) is such that the processes \(S^{i}(B^{\alpha })^{-1},\, i=1,2, \dots, d\) are \({\mathbb Q}^{\alpha }\)-martingales. For more information on the concept of a “martingale measure” in a nonlinear model, see Section 3.2.1 in Brigo et al. (2018). Equality (75) leads to the following formal additive decomposition of the ex-dividend price for \((A^{\sharp },\mathcal {X})\) into its clean price and several complementary valuation adjustments (for their interpretation, see Section 3.2.2 in Brigo et al. (2018)), which can be aggregated into a single total valuation adjustment, denoted as XVA t , so that we have
We stress that (76) is true for any choice for a proxy α for the risk-free interest rate, which further supports the view that the clean price is an abstract concept dissociated from the actual trading and the total valuation adjustment is a necessary mechanism needed to bring it back to reality. More importantly, terms appearing in the right-hand side in (76) are intertwined so that various valuation adjustments cannot be computed without the prior knowledge of the hedging strategy for the full contract. We thus conclude that the additivity and separation of adjustments, which is visibly suggested by the shape of equality (76), is in fact illusory, unless the underlying trading model has fully linear features so that it is possible to use the theory of linear BSDEs in order to justify separation. Obviously, this does not mean that separation cannot hold in some models with certain nonlinear features but this should be an exceptional situation, rather than the rule.
As a concrete example of an explicit application of nonlinear pricing theory, we may quote the recent paper by Bichuch et al. (2018) who provide a thorough examination of valuation of path-independent European claims in an extension of the classical Black-Scholes model to differential funding rates and counterparty credit risk (for another example of pricing under asymmetric borrowing and lending rates, see Brigo and Brigo and Pallavicini (2014). They first verify the no-arbitrage property of their trading model with respect to the null contract in the case of a nonnegative initial endowment x. Subsequently, they apply the BSDE approach to unilateral valuation of a collateralized European claim with bilateral default risk. The closeout payoff is specified in reference to the third party valuation, which is based on a single risk-free rate (not available to the two parties) and thus it is given by the standard Black-Scholes model. It is important to stress that the total valuation adjustment for the hedger (or the counterparty) is not computed in (Brigo and Pallavicini 2014) as a separate quantity, but it is instead defined as the difference between the full unilateral price and the Black-Scholes price (see Definition 4.8 in Bichuch et al. (2018), which is hence supposed to play the role of the clean price. Using our notation, the definition of the total valuation adjustment adopted in Bichuch et al. (2018) reads \(\text {XVA}_{t} := p^{e}_{t} (x,\mathcal {C}^{t}) - \pi ^{e,\alpha }_{t}(A)\). This means, of course, that Bichuch et al. (2018) do not advocate the practical approach where the clean price and valuations adjustment are supposed to be first independently computed by separate trading and CVA desks and subsequently aggregated into the full price. It is also observed in Bichuch et al. (2018) that the total valuation adjustments are equal and thus unilateral prices collapse to a single full price when the pricing BSDE is linear. Otherwise, the full prices computed independently by the two counterparties, who are supposed to use identical trading model, are likely to differ. Obviously, it is not our intention to suggest that the practice where separate desks are independently dealing with components of a contract and then using the aggregate number as a plausible candidate for the “full price” of a deal is wrong and thus should be eliminated. We have only argued that this practical approach, which is not hard to justify within the framework of a linear market (see, for instance, Burgard and Kjaer (2011,2013), Kenyon and Green (2014b, a) or Fujii and Takahashi (2013) is unlikely to result in theoretically correct arbitrage-free pricing in a nonlinear setup where the introduction of the concept of the clean price is no longer helpful.
Let us finally mention the important issue of netting of outstanding contracts between counterparties, which means that, in principle, every new deal should be valued not in isolation, but rather as a new component added to the portfolio of existing contracts. Needless to say, this issue is highly challenging, in both theory ad practice, and thus it is left for future work. Last but not least, it should be acknowledged that the valuation of derivatives based on arbitrage-free replication (or superhedging) should not be seen as the most realistic pricing approach, but rather a mathematical idealization of a much more complex situation, and thus other pricing paradigms should also be examined. The interested reader is referred to Kenyon and Green (2013) for a discussion of a regulatory-compliant derivatives pricing and to Albanese and Crépey (2017) for a novel balance-sheet approach to XVA with the special emphasis on KVA (capital value adjustment) computations.
Notes
The interested reader may consult the web pages http://www.investopedia.com/terms/s/shortsale.aspand https://www.sec.gov/investor/pubs/regsho.htmfor more details on the mechanics of short-sales.
We refer to https://www.newyorkfed.org/medialibrary/media/research/staff_reports/sr529.pdffor a detailed description of mechanics of repo trading.
References
Albanese, C, Crépey, S: XVA analysis from the balance sheet. Working paper (2017).
Albanese, C, Caenazzo, S, Crépey, S: Credit, funding, margin, and capital valuation adjustments for bilateral portfolios. Probability, Uncertainty and Quantitative Risk. 2(7), 1–26 (2017).
Bergman, YZ: Option pricing with differential interest rates. Review of Financial Studies. 8, 475–500 (1995).
Bichuch, M, et al.: Arbitrage-free XVA. Mathematical Finance. 28(2), 582–620 (2018).
Bielecki, TR, Rutkowski, M: Valuation and hedging of contracts with funding costs and collateralization. SIAM Journal of Financial Mathematics. 6, 594–655 (2015).
Bielecki, TR, Jeanblanc, M, Rutkowski, M: Hedging of defaultable claims. In: R. Carmona, et al. (eds.)Paris-Princeton Lectures on Mathematical Finance 2003, Lecture Notes in Mathematics, Vol. 1847, pp. 1–132. Springer, Berlin Heidelberg New York (2004).
Bielecki, TR, Jeanblanc, M, Rutkowski, M: Replication of contingent claims in a reduced-form credit risk model with discontinuous asset prices. Stochastic Models. 22, 661–687 (2006).
Bielecki, TR, Jeanblanc, M, Rutkowski, M: Credit Risk Modeling. Osaka University CSFI Lecture Notes Series. Osaka University Press, Osaka (2008).
Brigo, D, Pallavicini, A: Non-linear consistent valuation of CCP cleared or CSA bilateral trades with initial margins under credit, funding and wrong-way risks. Journal of Financial Engineering. 1, 1–60 (2014).
Brigo, D, Buescu, C, Rutkowski, M: Funding, repo and credit inclusive valuation as modified option pricing. Operations Research Letters. 45, 665–670 (2017).
Brigo, D, Buescu, C, Francischello, M, Pallavicini, A, Rutkowski, M: Risk-neutral valuation under differential funding costs, defaults and collateralization. Working paper (2018).
Burgard, C, Kjaer, M: Partial differential equations representations of derivatives with counterparty risk and funding costs. Journal of Credit Risk. 7, 1–19 (2011).
Burgard, C, Kjaer, M: Funding costs, funding strategies. Risk. 12(26), 82–87 (2013).
Carassus, L, Pham, H, Touzi, N: No arbitrage in discrete time under portfolio constraints. Mathematical Finance. 11, 315–329 (2001).
Carbone, R, Ferrario, B, Santacroce, M: Backward stochastic differential equations driven by càdlàg martingales. Theory of Probability and its Applications. 52, 304–314 (2008).
Cheridito, P, Nam, K: BSEs, BSDEs and fixed point problems. Annals of Probability. 45(6A), 3795–3828 (2017).
Crépey, S: Bilateral counterparty risk under funding constraints - Part I: Pricing. Mathematical Finance. 25, 1–22 (2015a).
Crépey, S: Bilateral counterparty risk under funding constraints - Part II: CVA. Mathematical Finance. 25, 23–50 (2015b).
Crépey, S, Song, S: Counterparty risk and funding: immersion and beyond. Finance and Stochastics. 20, 901–930 (2016).
Crépey, S, Song, S: Invariance times. Annals of Probability. 45(6B), 4632–4674 (2017).
Crépey, S, Bielecki, TR, Brigo, D: Counterparty Risk and Funding: A Tale of Two Puzzles. Chapman & Hall/CRC Financial Mathematics Series. CRC Press, Boca Raton, FL (2014).
Crépey, S, Elie, R, Sabbagh, W: When capital is the funding source: The XVA anticipated BSDEs. Working paper (2017).
Delbaen, F, Schachermayer, W: The Mathematics of Arbitrage. Springer, Berlin Heidelberg New York (2006).
Dumitrescu, R, Quenez, M. C, Sulem, A: Game options in an imperfect market with default. SIAM Journal on Financial Mathematics. 8, 532–559 (2017).
El Karoui, N, Huang, S. J: A general result of existence and uniqueness of backward stochastic differential equations. In: H. Brezis, et al. (eds.)Backward Stochastic Differential Equations. Pitman Research Notes in Mathematics Series, Vol. 364, pp. 27–36. Addison Wesley Longman, Harlow, Essex (1997).
El Karoui, N, Quenez, M. C: Non-linear pricing theory and backward stochastic differential equations. In: B. Biais, et al. (eds.)Financial Mathematics, Lecture Notes in Mathematics, Vol. 1656, pp. 191–246. Springer, Berlin Heidelberg New York (1997).
El Karoui, N, Peng, S, Quenez, M. C: Backward stochastic differential equation in finance. Mathematical Finance. 7, 1–71 (1997).
Fahim, A, Huang, Y: Model-independent superhedging under portfolio constraints. Finance and Stochastics. 20, 51–81 (2016).
Fontana, C: Weak and strong no-arbitrage conditions for continuous financial markets. International Journal of Theoretical and Applied Finance. 18, 1550005 (2015).
Fujii, M, Takahashi, A: Derivative pricing under asymmetric and imperfect collateralization and CVA. Quantitative Finance. 13(5), 749–768 (2013).
Karatzas, I, Kardaras, K: The numeraire portfolio in semimartingale financial models. Finance and Stochastics. 11, 447–493 (2007).
Karatzas, I, Kou, S: On the pricing of contingent claims under constraints. Annals of Applied Probability. 6, 321–369 (1996).
Karatzas, I, Kou, S: Hedging American contingent claims with constrained portfolios. Finance and Stochastics. 2, 215–258 (1998).
Kardaras, K: Market viability via absence of arbitrage of the first kind. Finance and Stochastics. 16, 651–667 (2012).
Kenyon, C, Green, A: Regulatory-compliant derivatives pricing is not risk-neutral. Working paper (2013).
Kenyon, C, Green, A: MVA: Initial margin valuation adjustment by replication and regression. Working paper (2014a).
Kenyon, C, Green, A: Warehousing credit (CVA) risk, capital (KVA) and tax (TVA) consequences. Working paper (2014b).
Korn, R: Contingent claim valuation in a market with different interest rates. Mathematical Methods of Operations Research. 42(3), 255–274 (1995).
Mercurio, F: Bergman, Piterbarg and beyond: Pricing derivatives under collateralization and differential rates. In: JA Londono, et al. (eds.)Actuarial Sciences and Quantitative Finance, Springer Proceedings in Mathematics and Statistics, Vol. 135, pp. 65–95. Springer, Berlin Heidelberg New York (2013).
Nie, T, Rutkowski, M: Fair bilateral prices in Bergman’s model with exogenous collateralization. International Journal of Theoretical and Applied Finance. 18, 1550048 (2015).
Nie, T, Rutkowski, M: A BSDE approach to fair bilateral pricing under endogenous collateralization. Finance and Stochastics. 20, 855–900 (2016a).
Nie, T, Rutkowski, M: BSDEs driven by a multi-dimensional martingale and their applications to market models with funding costs. Theory of Probability and its Applications. 60, 686–719 (2016b).
Nie, T, Rutkowski, M: Fair bilateral pricing under funding costs and exogenous collateralization. Mathematical Finance. 28(2), 621–655 (2018).
Pallavicini, A, Perini, D, Brigo, D: Funding, collateral and hedging: uncovering the mechanism and the subtleties of funding valuation adjustments. Working paper (2012a).
Pallavicini, A, Perini, D, Brigo, D: Funding valuation adjustment: a consistent framework including CVA, DVA, collateral, netting rules and re-hypothecation. Working paper (2012b).
Peng, S, Xu, X: BSDEs with random default time and their applications to default risk. Working paper (2009).
Piterbarg, V: Funding beyond discounting: collateral agreements and derivatives pricing. Risk. 23(2), 97–102 (2010).
Pulido, S: The fundamental theorem of asset pricing, the hedging problem and maximal claims in financial markets with short sales prohibitions. Annals of Applied Probability. 24, 54–75 (2014).
Quenez, MC, Sulem, A: BSDEs with jumps, optimization and applications to dynamic risk measures. Stochastic Processes and their Applications. 123, 3328–3357 (2013).
Takaoka, K, Schweizer, M: A note on the condition of no unbounded profit with bounded risk. Finance and Stochastics. 18, 393–405 (2014).
Zheng, S, Zong, G: A note on BSDEs and SDEs with time advanced and delayed coefficients. Working paper (2017).
Acknowledgements
The research of I. Cialenco and M. Rutkowski was supported by the DVC Research Bridging Support Grant BSDEs Approach to Models with Funding Costs. Part of the research was completed while I. Cialenco and M. Rutkowski were visiting the Institute for Pure and Applied Mathematics (IPAM) at UCLA, which is funded by the National Science Foundation. We would also like to thank the anonymous referees and Stéphane Crépey for their insightful and helpful comments and suggestions, which helped us greatly to improve the final manuscript.
Author information
Authors and Affiliations
Contributions
All authors read and approved the final manuscript.
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bielecki, T.R., Cialenco, I. & Rutkowski, M. Arbitrage-free pricing of derivatives in nonlinear market models. Probab Uncertain Quant Risk 3, 2 (2018). https://doi.org/10.1186/s41546-018-0027-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41546-018-0027-x
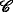 ,
,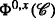 and
and 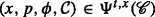 such that
such that 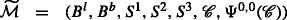 where S3=P(K) does not have the no-arbitrage property with respect to the null contract.
where S3=P(K) does not have the no-arbitrage property with respect to the null contract.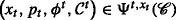 satisfying
satisfying
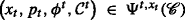 such that for some
such that for some 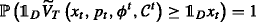
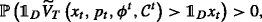
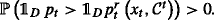
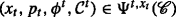 such that for some event
such that for some event 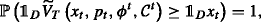
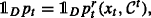 then
then