- Research
- Open access
- Published:
Continuous tenor extension of affine LIBOR models with multiple curves and applications to XVA
Probability, Uncertainty and Quantitative Risk volume 3, Article number: 1 (2018)
Abstract
We consider the class of affine LIBOR models with multiple curves, which is an analytically tractable class of discrete tenor models that easily accommodates positive or negative interest rates and positive spreads. By introducing an interpolating function, we extend the affine LIBOR models to a continuous tenor and derive expressions for the instantaneous forward rate and the short rate. We show that the continuous tenor model is arbitrage-free, that the analytical tractability is retained under the spot martingale measure, and that under mild conditions an interpolating function can be found such that the extended model fits any initial forward curve. This allows us to compute value adjustments (i.e. XVAs) consistently, by solving the corresponding ‘pre-default’ BSDE. As an application, we compute the price and value adjustments for a basis swap, and study the model risk associated to different interpolating functions.
Introduction
In the aftermath of the credit crisis and the European sovereign debt crisis, several of the classical paradigms in finance were no longer able to describe the new reality and needed to be designed afresh. On the one hand, significant spreads have appeared between rates of different tenors, which led to the development of multiple curve interest rate models. On the other hand, counterparty credit risk has emerged as the native form of default risk, along with liquidity risk, funding constraints and the collateralization of trades. Therefore, in post-crisis markets the quoted price of a derivative product (or, better, the cost of its hedging portfolio) is computed as the “clean” price of the product together with several value adjustments that reflect counterparty credit risk, liquidity risk, funding constraints, etc. In the context of interest rate derivatives, the “clean” price is typically computed as the discounted expected payoff under a martingale measure using a (discrete tenor) LIBOR market model, while the value adjustments are provided via the solution of a BSDE, which requires the existence of a short rate to discount the cash flows.
The aim of this work is to compute prices and value adjustments consistently, in the sense that we only calibrate a discrete tenor LIBOR model and then infer the dynamics of the short rate from it, instead of resorting to an additional, external short rate model. In the sequel, we will work with the class of affine LIBOR models with multiple curves. This class of models easily produces positive interest rates and positive spreads, as well as negative interest rates alongside positive spreads. Moreover, the models are analytically tractable in the sense that the driving process remains affine under all forward measures, which allows deriving of explicit expressions for the prices of caplets and semi-analytic expressions for swaptions. Thus, these models can be efficiently calibrated to market data; cf. Grbac et al. (2015) for more details.
Once the affine LIBOR model has been set up, we introduce an interpolating function that allows extending the model from a discrete to a continuous tenor, and derive explicit expressions for the dynamics of the instantaneous forward rate and of the short rate. This part follows and extends Keller-Ressel (2009), while a similar interpolation for affine LIBOR models has been recently introduced by Cuchiero et al. (2016). Moreover, we show that the resulting continuous tenor model is arbitrage-free and belongs to the class of affine term structure models. Let us mention that, on the contrary, the arbitrage-free interpolation of “classical” LIBOR market models is a challenging task; see e.g., Beveridge and Joshi (2012). In addition, we show that the driving process remains an affine process under the spot martingale measure, hence also the short rate is analytically tractable under this measure. The choice of the interpolating function is not innocuous though, as it may lead to undesirable behavior of the short rate; e.g., it may induce jumps at fixed times. Thus, we investigate what properties the (discrete tenor) affine LIBOR model and the interpolating function should have in order to avoid such situations. In particular, we show that under mild assumptions there exists an interpolating function such that the extended model can fit any initial forward curve.
Then, we can compute value adjustments via solutions of a “pre-default” BSDE using the framework of Crépey (2015a,b). As an illustration, we design and calibrate an affine LIBOR model, and consider a simple post-crisis interest rate derivative, namely a basis swap. Using the methodology outlined above, we derive the dynamics of the short rate and of the basis swap using an interpolating function, and compute the value adjustments for different specifications of the contract. As the choice of an interpolating function is still arbitrary, we study the model risk associated to different choices.
This paper is organized as follows: Section “Affine processes on \({\mathbb {R}}_{\geqslant 0}^{d}\)” reviews affine processes and Section “Affine LIBOR models with multiple curves” presents an overview of multiple curve markets and affine LIBOR models. Section “Continuous tenor extension of affine LIBOR models” focuses on the continuous tenor extension of affine LIBOR models and studies the properties of interpolating functions. The final Section “Computation of XVA in affine LIBOR models” outlines the computation of value adjustments in affine LIBOR models, and discusses the model risk associated with the choice of interpolating functions. The Appendix contains a useful result on the time integration of affine processes.
Affine processes on \({\mathbb {R}}_{\geqslant 0}^{d}\)
This section provides a brief overview of the basic notions and properties of affine processes. Proofs and further details can be found in Duffie et al. (2003), in Keller-Ressel (2008), and in Filipović (2005) for the time-inhomogeneous case.
Let  denote a complete stochastic basis in the sense of Jacod and Shiryaev (2003, Def. I.1.3), where \(\mathbb F=(\mathcal {F}_{t})_{t\in [0,T]}\) and T∈[0,∞) denotes the time horizon. In the sequel, we will consider a process X that satisfies the following:
denote a complete stochastic basis in the sense of Jacod and Shiryaev (2003, Def. I.1.3), where \(\mathbb F=(\mathcal {F}_{t})_{t\in [0,T]}\) and T∈[0,∞) denotes the time horizon. In the sequel, we will consider a process X that satisfies the following:
Assumption ( \(\mathbb {A}\) )
Let  be a conservative, time-homogeneous, stochastically continuous Markov process taking values in \(D=\mathbb {R}_{\geqslant 0}^{d}\), i.e.,
be a conservative, time-homogeneous, stochastically continuous Markov process taking values in \(D=\mathbb {R}_{\geqslant 0}^{d}\), i.e.,  is a family of probability measures on \((\Omega,\mathcal {F})\)and X=(X
t
)t∈[0,T] is a Markov process such that for every x∈D it holds X0=x,
is a family of probability measures on \((\Omega,\mathcal {F})\)and X=(X
t
)t∈[0,T] is a Markov process such that for every x∈D it holds X0=x,  -almost surely. Denote by
-almost surely. Denote by  the expectation w.r.t. the measure
the expectation w.r.t. the measure  and by 〈·,·〉 the inner product in \({\mathbb {R}}^{d}\). Setting
and by 〈·,·〉 the inner product in \({\mathbb {R}}^{d}\). Setting

we assume that
-
(i)
\(0\in \mathcal {I}_{T}^{\circ }\), where \(\mathcal I_{T}^{\circ }\) denotes the interior of \(\mathcal I_{T}\);
-
(ii)
The conditional moment generating function of X t under
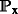 has exponentially-affine dependence on x; that is, there exist functions \(\phi \colon [0,T]\times \mathcal {I}_{T}\rightarrow \mathbb {R}\) and \(\psi \colon [0,T]\times \mathcal {I}_{T}\rightarrow {\mathbb {R}}^{d}\) such that
has exponentially-affine dependence on x; that is, there exist functions \(\phi \colon [0,T]\times \mathcal {I}_{T}\rightarrow \mathbb {R}\) and \(\psi \colon [0,T]\times \mathcal {I}_{T}\rightarrow {\mathbb {R}}^{d}\) such that
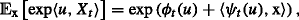 (1)
(1)for all \((t,u,x)\in [0,T]\times \mathcal {I}_{T}\times D\).
The functions ϕ and ψ satisfy the semi-flow equations, that is, for all 0≤t+s≤T and \(u\in \mathcal {I}_{T}\)
with initial conditions
Using the semi-flow equations we can derive the generalized Riccati equations
for \((t,u)\in [0,T]\times \mathcal {I}_{T}\), where F and R=(R1,…,R d ) are functions of Lévy–Khintchine form:
while (b,m,α i ,β i ,μ i )1≤i≤d are admissible parameters—see Definition 2.6 in Duffie et al. (2003) for details—and \(h_{i}\colon {\mathbb {R}_{\geqslant 0}}^{d}\rightarrow \mathbb {R}^{d}\) are suitable truncation functions. The infinitesimal generator of a process satisfying Assumption (\(\mathbb A\)) is provided by
for all \(f\in C_{0}^{2}(D)\) and x∈D.
Additional results are summarized in the following lemma. In the sequel, inequalities have to be understood componentwise, in the sense that (a1,a2)≤(b1,b2) if and only if a1≤b1 and a2≤b2.
Lemma 1
The functions ϕ and ψ satisfy the following:
-
1.
ϕ t (0)=ψ t (0)=0 for all t∈[0,T].
-
2.
\(\mathcal {I}_{T}\) is a convex set; moreover, for each t∈[0,T], the functions u↦ϕ t (u) and u↦ψ t (u), for \(u\in \mathcal {I}_{T}\), are (componentwise) convex.
-
3.
ϕ t (·) and ψ t (·) are order preserving: let \((t,u),\,(t,v)\in [0,T]\times \mathcal {I}_{T}\), with u≤v. Then
$$ \phi_{t}(u)\leq\phi_{t}(v) \quad \text{and} \quad \psi_{t}(u)\leq\psi_{t}(v). $$(6) -
4.
ψ t (·) is strictly order-preserving: let \((t,u),\,(t,v)\in [0,T]\times \mathcal {I}_{T}^{\circ }\), with u<v. Then ψ t (u)<ψ t (v).
-
5.
ϕ and ψ are jointly continuous on \([0,T]\times \mathcal {I}_{T}^{\circ }\).
-
6.
The partial derivatives
$$ \frac{\partial}{\partial u_{i}}\phi_{t}(u) \quad \text{and} \quad \frac{\partial}{\partial u_{i}}\psi_{t}(u),\quad i=1,\dots,d $$exist and are continuous for \(\left (t,u\right)\in [0,T]\times \mathcal {I}_{T}^{\circ }\).
Proof
See Keller-Ressel et al. (2013, Lem. 4.2) for statements (1)–(4) and Keller-Ressel (2008, Prop. 3.16 and Lem. 3.17) for the last two. □
Affine processes have rich structural properties which have been proved particularly useful when it comes to financial modeling. However, there are situations where the condition of time-homogeneity cannot be met; for example, time-inhomogeneity may be introduced through an equivalent change of measure. Filipović (2005) introduced time-inhomogeneous affine processes, whose conditional moment generating function takes the form

for all 0≤s≤t≤T and \(u\in \mathcal {I}_{T}\). Theorem 2.7 in Filipović (2005) yields that the infinitesimal generator is provided by

where the functions F and R retain the same form as in the time-homogeneous case, however, the (admissible) parameters are now time-dependent. If the process X is strongly regular affine—that is, the parameters satisfy some continuity conditions, see Definition 2.9 in Filipović (2005) for more details—then ϕs,t(u) and ψs,t(u) satisfy generalized Riccati equations with time-dependent functional characteristics F(s,u) and R(s,u), i.e., for all 0≤s≤t≤T
Affine LIBOR models with multiple curves
A multiple curve setting
We start by introducing some basic notation and the main concepts used in multiple curve LIBOR models, following the approach introduced by Mercurio (2010); see also Grbac et al. (2015) for an overview and more details.
The emergence of significant spreads between the OIS and LIBOR rates which depend on the investment horizon, also called tenor, means that we cannot work with a single tenor structure any longer. Let \(\mathcal {T}=\{0=T_{0}<T_{1}<\cdots <T_{N} = T\}\) denote a discrete, equidistant time structure where T k , for \(k\in \mathcal {K}=\{1,\dots,N\}\), denote the relevant market dates, e.g., payment dates and maturities of traded instruments. The set of tenors is denoted by \(\mathcal {X}=\{x_{1},\dots,x_{n}\}\), where we typically have \(\mathcal {X}=\{1,3,6,12\}\) months. Then, for every \(x\in \mathcal {X}\) we consider the corresponding tenor structure \(\mathcal {T}^{x}=\{0=T_{0}^{x}<T_{1}^{x}<\cdots <T_{N^{x}}^{x}=T_{N}\}\) with constant tenor length \(\delta _{x}=T_{k}^{x}-T_{k-1}^{x}\). We denote by \(\mathcal {K}^{x}=\{1,\dots,N^{x}\}\) the collection of all subscripts related to the tenor structure \(\mathcal {T}^{x}\), and assume that \(\mathcal {T}^{x}\subseteq \mathcal {T}\) for all \(x\in \mathcal {X}\).
The Overnight Indexed Swap (OIS) rate is regarded as the best market proxy for the risk-free interest rate. Moreover, the majority of traded interest rate derivatives are nowadays collateralized and the remuneration of the collateral is based on the overnight rate. Therefore, the discount factors B(0,T) are assumed to be stripped from OIS rates and defined for every possible maturity \(T\in \mathcal {T}\); see also Grbac and Runggaldier (2015, §1.3.1). B(t,T) denotes the discount factor, i.e., the time-t price of a zero coupon bond with maturity T, which is assumed to coincide with the corresponding OIS-based zero coupon bond.
Let  be a complete stochastic basis, where
be a complete stochastic basis, where  denotes the terminal forward measure, i.e., the martingale measure associated to the numeraire B(·,T
N
). We consider the forward measures
denotes the terminal forward measure, i.e., the martingale measure associated to the numeraire B(·,T
N
). We consider the forward measures  associated to the numeraires \(\{B(\cdot,T_{k}^{x})\}_{x,k}\) for every pair (x,k) with \(x\in \mathcal {X}\) and \(k\in \mathcal {K}^{x}\). Assuming that the processes \(B(\cdot,T_{k}^{x})/B(\cdot,T_{N})\) are true
associated to the numeraires \(\{B(\cdot,T_{k}^{x})\}_{x,k}\) for every pair (x,k) with \(x\in \mathcal {X}\) and \(k\in \mathcal {K}^{x}\). Assuming that the processes \(B(\cdot,T_{k}^{x})/B(\cdot,T_{N})\) are true  -martingales for every pair (x,k), the forward measures
-martingales for every pair (x,k), the forward measures  are absolutely continuous with respect to
are absolutely continuous with respect to  and defined in the usual way, i.e., via the Radon–Nikodym density
and defined in the usual way, i.e., via the Radon–Nikodym density

Therefore, the forward measures are associated to each other via

hence they are related to the terminal measure via

The expectations with respect to the forward measures  and the terminal measure
and the terminal measure  are denoted by
are denoted by  and
and  , respectively.
, respectively.
Next, we define the main modeling objects in the multiple curve LIBOR setting: the OIS forward rate, the forward LIBOR rate and the corresponding spread.
Definition 1
The time-tOIS forward rate for the time interval \([T_{k-1}^{x},T_{k}^{x}]\) is defined by
Definition 2
The time-tforward LIBOR rate for the time interval \([T_{k-1}^{x},T_{k}^{x}]\) is defined by

where \(L\left (T_{k-1}^{x},T_{k}^{x}\right)\) denotes the spot LIBOR rate at time \(T_{k-1}^{x}\) for the time interval \(\left [T_{k-1}^{x},T_{k}^{x}\right ]\).
The forward LIBOR rate is the rate implied by a forward rate agreement where the future spot LIBOR rate is exchanged for a fixed rate; cf. Mercurio (2009, pp. 12–13). The spot LIBOR rate \(L\left (T_{k-1}^{x},T_{k}^{x}\right)\) is set in advance, hence it is \({\mathcal {F}}_{T_{k-1}^{x}}\)-measurable, therefore we have that the forward LIBOR rate coincides with the spot LIBOR rate at the corresponding tenor dates, i.e.,

Definition 3
The (additive) spread between the forward LIBOR rate and the OIS forward rate is defined by
Remark 1
In a single curve setup, the forward LIBOR rate is defined via (11) and the spread equals zero for all times. However, in a multiple curve model these rates are not equal any more and we typically have that \(L_{k}^{x} \geq F_{k}^{x}\). \(F_{k}^{x}\) and \(L_{k}^{x}\) can also be interpreted as forward rates corresponding to a riskless and a risky bond, respectively; see e.g., Crépey et al. (2012).
Affine LIBOR models with multiple curves
We now turn our attention to the affine LIBOR models developed by Keller-Ressel et al. (2013) and extended to the multiple curve setting by Grbac et al. (2015). An important ingredient are martingales that are greater than, or equal to, one. Consider a process X satisfying Assumption (\(\mathbb {A}\)) and starting at the canonical value 1=(1,1,…,1), and let \(u\in \mathcal {I}_{T}\). Then, the process \({{M^{u}=(M^{u}_{t})_{t\in [0,T]}}}\) defined by

is a martingale. Moreover, if \(u\in \mathcal {I}_{T}\cap \mathbb {R}_{\geqslant 0}^{d}\) the mapping \(u \mapsto M_{t}^{u}\) is increasing and \(M^{u}_{t}\ge 1\) for every t∈[0,T]; see Keller-Ressel et al. (2013, Thm. 5.1) and Papapantoleon (2010).
The multiple curve affine LIBOR models are defined as follows:
Definition 4
A multiple curve affine LIBOR model \((X,\mathcal {X},T_{N},u,v)\) consists of the following elements:
-
An affine process X under
 satisfying Assumption (\(\mathbb {A}\)) and starting at the canonical value 1.
satisfying Assumption (\(\mathbb {A}\)) and starting at the canonical value 1. -
A set of tenors \(\mathcal {X}\).
-
A terminal maturity T N .
-
A sequence of vectors u=(u1,…,u N ) with \(u_{l}=:u_{k}^{x}\in \mathcal {I}_{T}\cap \mathbb {R}_{\geqslant 0}^{d}\), for all \(l=kT_{1}^{x}/T_{1}\) and \(x\in \mathcal {X}\), such that
$$ u_{1} \ge u_{2} \ge \cdots \ge u_{N}=0. $$(14) -
A collection of sequences of vectors \(v={\left \{(v_{1}^{x},\dots,v^{x}_{N^{x}})\right \}}_{x\in \mathcal {X}}\) with \(v_{k}^{x}\in \mathcal {I}_{T}\cap \mathbb {R}_{\geqslant 0}^{d}\), such that
$$ \begin{aligned} v_{k}^{x} \ge u_{k}^{x} \quad \text{for all}~ k\in\mathcal{K}^{x},x\in\mathcal{X}. \end{aligned} $$(15)
The dynamics of the OIS forward rates and the forward LIBOR rates in the model evolve according to
for all \(t\in [0,T_{k}^{x}]\), \(k\in \mathcal {K}^{x}\) and \(x\in \mathcal {X}\).
The definition of multiple curve affine LIBOR models implies that the dynamics of OIS forward rates and forward LIBOR rates, more precisely of \(1+\delta _{x}F_{k}^{x}\) and \(1+\delta _{x}L_{k}^{x}\), exhibit an exponential-affine dependence in the driving process X; see (13) and (16). Glau et al. (2016) recently showed that models that exhibit this exponential-affine dependence are the only ones that produce structure preserving LIBOR models; cf. Proposition 3.11 therein. The denominators in (16) are the same in both cases, since both rates have to be  -martingales by definition. On the other hand, different sequences \((u_{l})_{l\in \mathcal {K}}\) and \(\left (v_{k}^{x}\right)_{k\in \mathcal {K}^{x}}\) are used in the numerators in (16) producing different dynamics for OIS and LIBOR rates. These sequences are used to fit the multiple curve affine LIBOR model to a given initial term structure of OIS and LIBOR rates. In particular, the subsequent propositions show that by fitting the model to the initial term structure we automatically obtain sequences \((u_{l})_{l\in \mathcal {K}}\) and \((v_{k}^{x})_{k\in \mathcal {K}^{x}}\) that satisfy (14) and (15), respectively; see also Grbac et al. (2015, Rem. 4.4 and 4.5) for further comments on these sequences.
-martingales by definition. On the other hand, different sequences \((u_{l})_{l\in \mathcal {K}}\) and \(\left (v_{k}^{x}\right)_{k\in \mathcal {K}^{x}}\) are used in the numerators in (16) producing different dynamics for OIS and LIBOR rates. These sequences are used to fit the multiple curve affine LIBOR model to a given initial term structure of OIS and LIBOR rates. In particular, the subsequent propositions show that by fitting the model to the initial term structure we automatically obtain sequences \((u_{l})_{l\in \mathcal {K}}\) and \((v_{k}^{x})_{k\in \mathcal {K}^{x}}\) that satisfy (14) and (15), respectively; see also Grbac et al. (2015, Rem. 4.4 and 4.5) for further comments on these sequences.
The following quantity measures the ability of a multiple curve affine LIBOR model to fit a given initial term structure

In several models commonly used in mathematical finance, such as the Cox–Ingersoll–Ross model and Ornstein–Uhlenbeck processes driven by subordinators, this quantity equals infinity. The following propositions show that the affine LIBOR models are well-defined and can fit any initial term structure under mild conditions.
Proposition 1
Consider the time structure \(\mathcal {T}\), let B(0,T l ), \(l\in \mathcal {K}\), be the initial term structure of OIS discount factors and assume that
Then, the following hold:
-
1.
If γ X >B(0,T1)/B(0,T N ), there exists a sequence \((u_{l})_{l\in \mathcal {K}}\) in \(\mathcal {I}_{T}\cap \mathbb {R}_{\geqslant 0}^{d}\) satisfying (14) such that
$$ M_{0}^{u_{l}} = \frac{B(0,T_{l})}{B(0,T_{N})}\quad\text{for all }l\in\mathcal{K}. $$In particular, if γ X =∞, then the multiple curve affine LIBOR model can fit any initial term structure of OIS rates.
-
2.
If X is one-dimensional, the sequence \((u_{l})_{l\in \mathcal {K}}\) is unique.
-
3.
If all initial OIS rates are positive, the sequence \((u_{l})_{l\in \mathcal {K}}\) is strictly decreasing.
Proof
See Proposition 6.1 in Keller-Ressel et al. (2013). □
Proposition 2
Consider the setting of the previous proposition, fix \(x\in \mathcal {X}\) and the corresponding tenor structure \(\mathcal {T}^{x}\). Let \(L_{k}^{x}(0)\), \(k\in \mathcal {K}^{x}\), be the initial term structure of non-negative forward LIBOR rates and assume that for every \(k\in \mathcal {K}^{x}\)
Then, the following hold:
-
1.
If \(\gamma _{X}>(1+\delta _{x}L_{k}^{x}(0))B(0,T_{k}^{x})/B(0,T_{N})\) for all \(k\in \mathcal {K}^{x}\), then there exists a sequence \((v_{k}^{x})_{k\in \mathcal {K}^{x}}\) in \({\mathcal {I}}_{T}\cap {\mathbb {R}_{\geqslant 0}}^{d}\) satisfying (15) such that
$$ M_{0}^{v_{k}^{x}} = \left(1+\delta_{x}L_{k+1}^{x}(0)\right) M_{0}^{u_{k+1}^{x}}, \quad \text{for all}~ k\in\mathcal{K}^{x}\setminus\{N^{x}\}. $$In particular, if γ X =∞, then the multiple curve affine LIBOR model can fit any initial term structure of forward LIBOR rates.
-
2.
If X is one-dimensional, the sequence \((v_{k}^{x})_{k\in \mathcal {K}^{x}}\) is unique.
-
3.
If all initial LIBOR-OIS spreads are positive (i.e., (19) becomes strict), then \(v_{k}^{x}>u_{k}^{x}\), for all \(k\in \mathcal {K}^{x}\setminus \{N^{x}\}\).
Proof
See Proposition 4.2 in Grbac et al. (2015). □
Remark 2
The proofs of these propositions are constructive and provide an easy algorithm for fitting an affine LIBOR model to a given initial term structure of OIS and LIBOR rates. However, for d>1 the sequences u and vx are not unique, hence questions about optimality arise; see the discussion in Subsections “On the choice of the interpolating function” and “Discussion”. In the proof of Proposition 1, the sequence \((u_{l})_{l\in \mathcal {K}}\) is chosen along a straight line in \(\mathcal {I}_{T}\cap \mathbb {R}^{d}_{\geqslant 0}\) from some \(u\in \mathcal {I}_{T}\) to 0, such that u satisfies

However, any other continuous path from another u′ to 0, that satisfies (20) and is componentwise decreasing, would have worked as well.
The next proposition shows that multiple curve affine LIBOR models are analytically tractable, in the sense that the affine structure is preserved under any forward measure.
Proposition 3
The underlying process X is a time-inhomogeneous affine process under the measure  , for every \(x\in \mathcal {X}\) and \(k\in \mathcal {K}^{x}\). The moment generating function is provided by
, for every \(x\in \mathcal {X}\) and \(k\in \mathcal {K}^{x}\). The moment generating function is provided by

for every w such that \(w+\psi _{T_{N}-t}(u_{k}^{x})\in \mathcal {I}_{T}\), where
Proof
See Proposition 4.6 in Grbac et al. (2015). □
The multiple curve affine LIBOR models defined above and satisfying the prerequisites of Propositions 1 and 2 are arbitrage-free discrete tenor models, in the sense that \(F_{k}^{x}\) and \(L_{k}^{x}\) are  -martingales for every \(k\in \mathcal {K}^{x}\), \(x\in \mathcal {X}\), while the interest rates and the spread are positive, i.e., \(F_{k}^{x}(t)\ge 0\) and \(S_{k}^{x}(t)=L_{k}^{x}(t)-F_{k}^{x}(t)\ge 0\) for every \(t\in [0,T_{k-1}^{x}], k\in \mathcal {K}^{x}\), \(x\in \mathcal {X}\); cf. Proposition 4.3 in Grbac et al. (2015).
-martingales for every \(k\in \mathcal {K}^{x}\), \(x\in \mathcal {X}\), while the interest rates and the spread are positive, i.e., \(F_{k}^{x}(t)\ge 0\) and \(S_{k}^{x}(t)=L_{k}^{x}(t)-F_{k}^{x}(t)\ge 0\) for every \(t\in [0,T_{k-1}^{x}], k\in \mathcal {K}^{x}\), \(x\in \mathcal {X}\); cf. Proposition 4.3 in Grbac et al. (2015).
Remark 3
The class of affine LIBOR models with multiple curves can be extended to accommodate negative interest rates alongside positive spreads; see Grbac et al. (2015, §4.1) for the details.
Remark 4
We could use time-dependent parameters, i.e., time-inhomogeneous affine processes, in the construction of affine LIBOR models, in particular since the dynamics of X are time-dependent under forward measures; see Proposition 3. We use affine processes instead, in order to ease the presentation of the model and its properties, and to be consistent with the relevant literature (cf. Keller-Ressel et al. 2013 and Grbac et al. 2015).
Continuous tenor extension of affine LIBOR models
Discrete to continuous tenor
This section is devoted to the extension of the affine LIBOR models from a discrete to a continuous tenor structure, and the derivation of the dynamics of the corresponding instantaneous forward rate and short rate. The main tool is an interpolating function  , which is a function defined on [0,T
N
] that matches u
l
at each tenor date T
l
. This subsection follows and extends Keller-Ressel (2009).
, which is a function defined on [0,T
N
] that matches u
l
at each tenor date T
l
. This subsection follows and extends Keller-Ressel (2009).
Definition 5
An interpolating function for the multiple curve affine LIBOR model \((X,\mathcal {X},T_{N},u,v)\) is a continuous, componentwise decreasing function  with
with  for all t∈[0,T
N
] and bounded right-hand derivatives, such that
for all t∈[0,T
N
] and bounded right-hand derivatives, such that  for all \(T_{l}\in \mathcal {T}\).
for all \(T_{l}\in \mathcal {T}\).
Remark 5
Since  is a mapping from [0,T
N
], it makes sense to define a
is a mapping from [0,T
N
], it makes sense to define a  element. This can be chosen such that
element. This can be chosen such that  which is consistent with Proposition 1.
which is consistent with Proposition 1.
The interpolating function allows deriving of an explicit expression for the dynamics of zero coupon bond prices in the multiple curve affine LIBOR model. In particular, they belong to the class of affine term structure models; see e.g., Björk (2009, §24.3).
Lemma 2
Let  be an interpolating function for the multiple curve affine LIBOR model \((X,\mathcal {X},T_{N},u,v)\) and define the (OIS zero coupon) bond price B(t,T) by
be an interpolating function for the multiple curve affine LIBOR model \((X,\mathcal {X},T_{N},u,v)\) and define the (OIS zero coupon) bond price B(t,T) by

for 0≤t≤T≤T
N
, where  is the martingale defined by (13). Then, bond prices satisfy
is the martingale defined by (13). Then, bond prices satisfy

where

Proof
Using the definition of the OIS forward rate, (16), and the positivity of bond prices, we get in the discrete tenor case,
for every \(T_{k},T_{i}\in \mathcal {T}\) such that T k ≤T i ≤T N . Similarly in the continuous tenor case, using (21) we get for 0≤t≤T≤T N that

where ⌊t⌋ is such that T⌊t⌋ is the largest element in the time structure \(\mathcal {T}\) less than or equal to t. Hence, since  depends exponentially-affine on X
t
, we arrive at (22)–(23). □
depends exponentially-affine on X
t
, we arrive at (22)–(23). □
Next, we will show that the extension of an affine LIBOR model from a discrete to a continuous tenor is an arbitrage-free term structure model. Following Musiela and Rutkowski (1997, Def. 2.3), we say that a family of bond prices  satisfies a no-arbitrage condition if there exists a measure
satisfies a no-arbitrage condition if there exists a measure  such that
such that  is a
is a  -local martingale and
-local martingale and  for any
for any 
Theorem 1
Let  be an interpolating function for the multiple curve affine LIBOR model \((X,\mathcal {X},T_{N},u,v)\). Then,
be an interpolating function for the multiple curve affine LIBOR model \((X,\mathcal {X},T_{N},u,v)\). Then,  is a continuous tenor extension of the affine LIBOR model, i.e., an arbitrage-free model for all maturities
is a continuous tenor extension of the affine LIBOR model, i.e., an arbitrage-free model for all maturities  , such that for all maturities \(T\in \mathcal {T}\) the bond prices coincide with those of the (discrete tenor) affine LIBOR model.
, such that for all maturities \(T\in \mathcal {T}\) the bond prices coincide with those of the (discrete tenor) affine LIBOR model.
Proof
The definition of the interpolating function yields immediately that bond prices in the continuous tenor extension coincide with those of the discrete tenor affine LIBOR model for all maturities.
According to Musiela and Rutkowski (1997, §2.3), in order to show that the model is arbitrage-free it suffices to verify the following conditions on the family  of bond prices:
of bond prices:
-
(i)
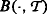 is a strictly positive special semimartingale and the left-hand limit process
is a strictly positive special semimartingale and the left-hand limit process 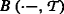 is also strictly positive, for every
is also strictly positive, for every 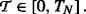
-
(ii)
The bond price quotients
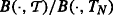 are
are 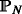 -martingales.
-martingales. -
(iii)
B(t,S)≤B(t,U) for all 0≤t≤S≤U≤T N .
The second condition follows immediately from (21) and the construction of Mu as a  -martingale. In order to check the first and the third conditions, we shall use the representation for the bond prices from Lemma 2. Indeed, the last condition follows directly from representation (22)–(23), using the monotonicity of the function
-martingale. In order to check the first and the third conditions, we shall use the representation for the bond prices from Lemma 2. Indeed, the last condition follows directly from representation (22)–(23), using the monotonicity of the function  and the order preserving property of ϕ and ψ; cf. Lemma 1. Moreover, the continuity of ϕ and ψ together with (22) imply that
and the order preserving property of ϕ and ψ; cf. Lemma 1. Moreover, the continuity of ϕ and ψ together with (22) imply that  which ensures the positivity of
which ensures the positivity of 
Finally,  is a smooth function of X hence it is also a semimartingale, which is special if its associated jump process
is a smooth function of X hence it is also a semimartingale, which is special if its associated jump process  is absolutely bounded; cf. Jacod and Shiryaev (2003, Lem. I.4.24). The processes X and X− are non-negative a.s. and the same is true for ΔX, since the compensator of the jump measure of X is entirely supported on the positive half-space; cf. Duffie et al. (2003, Def. 2.6). Using again Lemma 1 (4) and the monotonicity of
is absolutely bounded; cf. Jacod and Shiryaev (2003, Lem. I.4.24). The processes X and X− are non-negative a.s. and the same is true for ΔX, since the compensator of the jump measure of X is entirely supported on the positive half-space; cf. Duffie et al. (2003, Def. 2.6). Using again Lemma 1 (4) and the monotonicity of  we get that
we get that  and
and  take values in the negative half space. Thus, we can estimate the jump process
take values in the negative half space. Thus, we can estimate the jump process  as follows:
as follows:

□
Having bond prices for all maturities  at hand, we can now calculate the dynamics of the instantaneous forward rate
at hand, we can now calculate the dynamics of the instantaneous forward rate  with maturity
with maturity  prevailing at time t and of the short rate r
t
prevailing at time t. These quantities are commonly defined as
prevailing at time t and of the short rate r
t
prevailing at time t. These quantities are commonly defined as

Together with the requirement that  we get that the former is equivalent to
we get that the former is equivalent to

Lemma 3
Let  be an interpolating function and consider the continuous tenor extension of the affine LIBOR model \({(X,\mathcal {X},T_{N},u,v)}\). Then, the instantaneous forward rate and the short rate are provided by
be an interpolating function and consider the continuous tenor extension of the affine LIBOR model \({(X,\mathcal {X},T_{N},u,v)}\). Then, the instantaneous forward rate and the short rate are provided by

where

for all  Here, a∘b denotes the componentwise multiplication of two vectors a and b having the same dimension.
Here, a∘b denotes the componentwise multiplication of two vectors a and b having the same dimension.
Proof
We know from Lemma 2 that bond prices are log-affine functions of X, in particular they are provided by (22)–(23). The result now follows by taking the right-hand derivative of  w.r.t.
w.r.t.  , which exists by Definition 5 and Lemma 1(6). Note also that
, which exists by Definition 5 and Lemma 1(6). Note also that  and
and  are positive, for all
are positive, for all  □
□
Moreover, the continuously compounded bank account B⋆ is defined as usual:
while the associated spot measure  , under which bond prices are provided by
, under which bond prices are provided by

is calculated next.
Lemma 4
Let  be an interpolating function and consider the continuous tenor extension of the affine LIBOR model \({(X,\mathcal {X},T_{N},u,v)}\). Then, the spot measure
be an interpolating function and consider the continuous tenor extension of the affine LIBOR model \({(X,\mathcal {X},T_{N},u,v)}\). Then, the spot measure  is determined by the density process
is determined by the density process

where  and
and  .
.
Proof
The spot measure and the terminal forward measure are related via

cf. Musiela and Rutkowski (2005, §13.2.2). Then, the representation above follows easily from (28), (22)–(23), Lemma 1(1), and Remark 5, using the fact that  hence
hence  □
□
The next result resembles Proposition 3 and shows that the driving process X remains an affine process under the spot measure  . In other words, the multiple curve affine LIBOR model remains analytically tractable under the spot measure as well.
. In other words, the multiple curve affine LIBOR model remains analytically tractable under the spot measure as well.
Theorem 2
Let  be an interpolating function and consider the continuous tenor extension of the affine LIBOR model \({(X,\mathcal {X},T_{N},u,v)}\). Then the underlying process X is a time-inhomogeneous affine process under the spot measure
be an interpolating function and consider the continuous tenor extension of the affine LIBOR model \({(X,\mathcal {X},T_{N},u,v)}\). Then the underlying process X is a time-inhomogeneous affine process under the spot measure  . In particular, X is strongly regular affine and the functional characteristics under
. In particular, X is strongly regular affine and the functional characteristics under  are provided by
are provided by
for every w such that \(w+Q_{t}\in \mathcal {I}_{T}\).
Proof
We will first show that the moment generating function of X has an exponential-affine form under  . Starting from the moment generating function of X under
. Starting from the moment generating function of X under  , and using the conditional density process in Lemma 4 and the dynamics of the short rate process in (26)–(27), we arrive at
, and using the conditional density process in Lemma 4 and the dynamics of the short rate process in (26)–(27), we arrive at

Theorem 4.10 in Keller-Ressel (2008) provides an elegant way to calculate the functional characteristics of a time integrated affine process. This result is proved for \(Y_{\cdot }=\int _{0}^{\cdot } X_{u} \mathrm {d} u\) and is extended to \(\widetilde {Y}_{\cdot }=\big (\int _{0}^{\cdot } \theta _{u}^{i}X_{u}^{i} \mathrm {d} u\big)_{1\le i\le d}\) for a deterministic, bounded and positive θ in Theorem 3 of the appendix. Then, we have that the functional characteristics of the joint process \(\left (X_{t},\widetilde {Y}_{t}\right)\) are provided by
The definition of the interpolating function together with Lemma 1 (6) yield that q in (27) is bounded. Hence, applying Theorem 3 yields that B in (29) takes the form
where \(\widetilde {\phi }\) and \(\widetilde {\psi }\) are the solutions of the generalized Riccati equations defined by \(\widetilde {F}\) and \(\widetilde {R}\); cf. (3). The form of \(\widetilde {R}\) implies that the components of \(\widetilde {\psi }\) corresponding to \(\widetilde {Y}\) satisfy \(\widetilde {\psi }_{t-s}(w_{x},w_{y})_{y}=w_{y}\). Hence, we get from (29) that

Now, conditioning on X
s
=x and taking the right-hand derivatives with respect to s at t=s, we arrive at the generator of X under  :
:
compare with (7). The semigroup of the affine process X under  is weakly regular in the sense of Filipović (2005, Def. 2.3), since the process X is stochastically continuous under
is weakly regular in the sense of Filipović (2005, Def. 2.3), since the process X is stochastically continuous under  and the generator exists and is continuous at w=0 for all (t,x)∈[0,T]×D. Moreover, X is strongly regular affine under
and the generator exists and is continuous at w=0 for all (t,x)∈[0,T]×D. Moreover, X is strongly regular affine under  since the weakly admissible parameters (α⋆(t),b⋆(t),β⋆(t),m⋆(t),μ⋆(t)) implied by (30) are continuous transformations of (α,b,β,m,μ). □
since the weakly admissible parameters (α⋆(t),b⋆(t),β⋆(t),m⋆(t),μ⋆(t)) implied by (30) are continuous transformations of (α,b,β,m,μ). □
Using the last proposition, we get that the conditional moment generating function of X under  is given by
is given by

where \(\phi _{s,t}^{\star }\) and \(\psi _{s,t}^{\star }\) are the solutions of the generalized Riccati equations with functional characteristics F⋆ and R⋆; cf. (8). Since both the instantaneous forward rate and the short rate are time-dependent affine transformations of the driving process X, they will inherit many (distributional) properties from X. In fact, once we have computed the characteristics of the driving process X under the spot measure  , it is easy to see that also the short rate r has time-inhomogeneous characteristics, that are affine w.r.t. X. Indeed, from (26) and (31) we get
, it is easy to see that also the short rate r has time-inhomogeneous characteristics, that are affine w.r.t. X. Indeed, from (26) and (31) we get

On the choice of the interpolating function
The requirements on the interpolating function  are rather weak, such that even a linear interpolation between the u
k
’s corresponding to the maturities T
k
, \(k\in \mathcal K\), can be used. However, looking at Eqs. (26)–(27) for the dynamics of the short rate process r, we can immediately observe that jumps will occur at fixed times, the maturities T
k
, if
are rather weak, such that even a linear interpolation between the u
k
’s corresponding to the maturities T
k
, \(k\in \mathcal K\), can be used. However, looking at Eqs. (26)–(27) for the dynamics of the short rate process r, we can immediately observe that jumps will occur at fixed times, the maturities T
k
, if  is not continuously differentiable. A more sophisticated, but still arbitrary, choice for an interpolating function are cubic splines, i.e., piecewise polynomials of degree three, which are continuously differentiable and thus do not lead to deterministic discontinuities; see Fig. 1 for an illustration.
is not continuously differentiable. A more sophisticated, but still arbitrary, choice for an interpolating function are cubic splines, i.e., piecewise polynomials of degree three, which are continuously differentiable and thus do not lead to deterministic discontinuities; see Fig. 1 for an illustration.
The next corollary is an immediate consequence of Lemma 3 and the fact that X is stochastically continuous.
Corollary 1
Let  be a continuously differentiable interpolating function, i.e.,
be a continuously differentiable interpolating function, i.e.,  , and consider the continuous tenor extension of the affine LIBOR model \({(X,\mathcal {X},T_{N},u,v)}\). Then the short rate process r is stochastically continuous.
, and consider the continuous tenor extension of the affine LIBOR model \({(X,\mathcal {X},T_{N},u,v)}\). Then the short rate process r is stochastically continuous.
However, even when the interpolating function is continuously differentiable there can be sources of undesirable behavior of the short rate inherited from the sequence (u k ) itself (which is not unique unless d=1; cf. Remark 2). Consider, for example, the following “diagonal” structure for (u k ), which is similar to the one employed by Grbac et al. (2015) to model independence between rates of different maturities:

with \(\bar {u}_{i}\in \mathbb {R}_{\geqslant 0}\), for 1≤i≤N. The only paths that can be used to interpolate in this case are the ones connecting the elements u k and uk+1 of the sequence (u k ) via straight lines, otherwise the interpolating function will not be component-wise decreasing. Hence, any interpolating function maps onto a non-smooth manifold. Then, requiring that the interpolating function is continuously differentiability (in time) will lead to a short rate that drops to zero at every T k , \(k\in \mathcal {K}\), since the derivative of the interpolating function will equal zero at each T k ; see again (26) and (27), and the illustration in Fig. 2.
We would like in the sequel to provide conditions such that the short rate resulting from a continuous tenor extension of an affine LIBOR model exhibits “reasonable” behavior, in the sense that it neither jumps at fixed times, nor drops to zero at each maturity date. Moreover, we would like to identify a method for choosing an interpolating function that removes the arbitrariness from this choice. A condition for the former is that the sequence \((u_{k})_{k\in \mathcal {K}}\) lies on a smooth manifold. Regarding the latter, we could require that a continuum of bond prices are fitted as well. These together lead to a uniquely defined, continuously differentiable interpolating function.
Example 1
Let \({(X,\mathcal {X},T_{N},u,v)}\) be an affine LIBOR model and assume that the sequence \((u_{k})_{k\in \mathcal {K}}\) admits an interpolating function \(\hat {{U}}\) that maps onto a smooth manifold  Moreover, let \(\tilde {f}(0,\cdot)\colon [0,T_{N}]\rightarrow \mathbb {R}_{\geqslant 0}\) be an initial forward curve—belonging, e.g., to the Nelson–Siegel or Svensson family—that is consistent with the initial bond prices, i.e.,
Moreover, let \(\tilde {f}(0,\cdot)\colon [0,T_{N}]\rightarrow \mathbb {R}_{\geqslant 0}\) be an initial forward curve—belonging, e.g., to the Nelson–Siegel or Svensson family—that is consistent with the initial bond prices, i.e.,
Then, we can find an interpolating function  such that the continuous-tenor extended affine LIBOR model fits the given initial forward curve \(\tilde f\). In order to achieve this, the interpolating function
such that the continuous-tenor extended affine LIBOR model fits the given initial forward curve \(\tilde f\). In order to achieve this, the interpolating function  should satisfy the following:
should satisfy the following:

for all  This equation follows directly from the requirement that (34) holds for all
This equation follows directly from the requirement that (34) holds for all  together with (22)–(23) and Remark 5. Moreover, the dynamics of the instantaneous forward rate are provided by (26)–(27) for all T∈[0,T
N
], and satisfy the initial condition
together with (22)–(23) and Remark 5. Moreover, the dynamics of the instantaneous forward rate are provided by (26)–(27) for all T∈[0,T
N
], and satisfy the initial condition 
The curve fitting problem in (35) can be solved analogously to the problem of fitting the sequence (u k ) to an initial term structure of bond prices; compare with Proposition 6.1 in Keller-Ressel et al. (2013) and the corresponding proof. The resulting interpolating function is then differentiable with respect to time, as the following result shows.
Proposition 4
Let \({(X,\mathcal {X},T_{N},u,v)}\) be a multiple curve affine LIBOR model, assume that \(\tilde f(0,\cdot):[0,T_{N}]\to \mathbb {R}_{\geqslant 0}\) is continuous and that \((u_{k})_{k\in \mathcal {K}}\) allows for an interpolating function that maps onto a C1-manifold  Then, there exists a unique continuously differentiable interpolating function
Then, there exists a unique continuously differentiable interpolating function  satisfying (35).
satisfying (35).
Proof
This statement is an easy consequence of the implicit function theorem, where the differentiability of ϕ and ψ in space and time as well as their order preserving property (cf. Lemma 1) are used. Indeed, the function
is continuously differentiable in t∈[0,T
N
] and \(u\in \mathcal {I}_{T}\). Let  be an atlas for the C1-manifold
be an atlas for the C1-manifold  , where
, where  is a finite index set,
is a finite index set,  is an open covering of
is an open covering of  and \(g_{\alpha }:U_{\alpha }\rightarrow I_{\alpha }\subseteq \mathbb {R}\) is a C1-homeomorphism. Define \(G^{\star }\colon [0,T_{N}]\times I_{\alpha }\rightarrow {\mathbb {R}}\) by \({\left (t,x\right)}\mapsto G{\left (t,g^{-1}_{\alpha {\left (x\right)}}\right)}\). By the (strict) order preserving property of ϕ and ψ we know that the partial derivative \(\frac {\partial }{\partial x}G^{\star {\left (t,x\right)}}\) is not zero, hence by a compactness argument there exists a unique continuously differentiable function \(x\colon [0,T_{N}]\rightarrow \mathbb {R}\) such that G⋆(t,x(t))=0 for all t∈[0,T
N
]. The interpolating function is then given by
and \(g_{\alpha }:U_{\alpha }\rightarrow I_{\alpha }\subseteq \mathbb {R}\) is a C1-homeomorphism. Define \(G^{\star }\colon [0,T_{N}]\times I_{\alpha }\rightarrow {\mathbb {R}}\) by \({\left (t,x\right)}\mapsto G{\left (t,g^{-1}_{\alpha {\left (x\right)}}\right)}\). By the (strict) order preserving property of ϕ and ψ we know that the partial derivative \(\frac {\partial }{\partial x}G^{\star {\left (t,x\right)}}\) is not zero, hence by a compactness argument there exists a unique continuously differentiable function \(x\colon [0,T_{N}]\rightarrow \mathbb {R}\) such that G⋆(t,x(t))=0 for all t∈[0,T
N
]. The interpolating function is then given by  □
□
Remark 6
Figure 1 reveals another interesting behavior of the short rate implied by an affine LIBOR model. In particular, there exists a lower bound for the short rate that is greater than zero. Indeed, since the state space of our driving affine process is \(\mathbb {R}_{\geqslant 0}^{d}\), we have that r t ≥p t , which is greater than zero as ϕ is strictly order preserving and u is decreasing. A similar phenomenon was already observed in the discrete tenor model for the LIBOR rate, compare with Keller-Ressel et al. (2013, Rem. 6.4).
Computation of XVA in affine LIBOR models
The quoted price of a derivative product in pre-crisis markets was equal to its discounted expected payoff (under a martingale measure), since counterparties were considered default-free, there was abundance of liquidity in the markets, and other frictions were also negligible. In post-crisis markets, however, these assumptions have been challenged; in particular, counterparty credit risk has emerged as the natural form of default risk, there is shortage of liquidity in financial markets, while other frictions have also gained importance. These facts have thus to be factored into the quoted price. One way to do that, is to compute first the so-called “clean” price of the derivative, which equals its discounted expected payoff (under a martingale measure), and then add to it several value adjustments, collectively abbreviated as XVA, that reflect counterparty credit risk, liquidity costs, etc. We refer to Brigo et al. (2013), Crépey (2015a,b), Crépey and Bielecki (2014), and Bichuch et al. (2016) among others for more details on XVA.
Clean valuation
This section reviews basis swaps and provides formulas for their clean price in affine LIBOR models with multiple curves. The clean valuation of caps, swaptions, and basis swaptions in these models is extensively studied in Grbac et al. (2015).
The typical example of an interest rate swap is where a floating rate is exchanged for a fixed rate; see, e.g., Musiela and Rutkowski (2005, §9.4). The appearance of significant spreads between rates of different tenors has given rise to a new kind of interest rate swap, called basis swap, where two streams of floating payments linked to underlying rates of different tenors are exchanged. As an example, in a 3M-6M basis swap linked to the LIBOR, the 3-month LIBOR is paid quarterly and the 6-month LIBOR is received semiannually.
Let \(\mathcal {T}_{p_{1}q_{1}}^{x_{1}} = \left \{T_{p_{1}}^{x_{1}},\dots,T_{q_{1}}^{x_{1}}\right \}\) and \(\mathcal {T}_{p_{2}q_{2}}^{x_{2}} = \left \{T_{p_{2}}^{x_{2}},\dots,T_{q_{2}}^{x_{2}}\right \}\) denote two tenor structures, where \(T_{p_{1}}^{x_{1}}=T_{p_{2}}^{x_{2}}\), \(T_{q_{1}}^{x_{1}}=T_{q_{2}}^{x_{2}}\), and \(\mathcal {T}_{p_{2}q_{2}}^{x_{2}}\subset \mathcal {T}_{p_{1}q_{1}}^{x_{1}}\). Consider a basis swap that is initiated at \(T_{p_{1}}^{x_{1}}=T_{p_{2}}^{x_{2}}\), with the first payments due at \(T_{p_{1}+1}^{x_{1}}\) and \(T_{p_{2}+1}^{x_{2}}\), respectively. In order to reflect the possible discrepancy between the floating rates at initiation, the interest rate \(L\left (T_{i-1}^{x_{1}},T_{i}^{x_{1}}\right)\) corresponding to the shorter tenor length x1 is replaced by \(L\left (T_{i-1}^{x_{1}},T_{i}^{x_{1}}\right)+S\) for a fixed S, which is called the basis swap spread. The time-r value of a basis swap with notional amount normalized to 1, for \(0\le r\le T_{p_{1}}^{x_{1}}\), is given by

The fair basis swap spread \(S_{r}\left (\mathcal {T}_{p_{1}q_{1}}^{x_{1}},\mathcal {T}_{p_{2}q_{2}}^{x_{2}}\right)\) is then computed so that the value of the swap at inception is zero, i.e., \(\mathbb {BS}_{r}\left (S,\mathcal {T}_{p_{1}q_{1}}^{x_{1}},\mathcal {T}_{p_{2}q_{2}}^{x_{2}}\right)=0\) for \(0\leq r\leq T_{p_{1}}^{x_{1}}\). Hence, the fair spread is given by
Moreover, the time-t value of the basis swap, for \(t\in \left [T_{p_{1}}^{x_{1}},T_{q_{2}}^{x_{2}}\right ]\), using (16) and (24), takes the form:

where \(S_{r}=S_{r}\left (\mathcal {T}_{p_{1}q_{1}}^{x_{1}},\mathcal {T}_{p_{2}q_{2}}^{x_{2}}\right)\), for \(r\in \left [0,T_{p_{1}}^{x_{1}}\right ]\) being the date of inception, while \(\lceil t \rceil _{i} = \min \left \{ k\in \mathcal {K}^{x_{i}}: t<T_{k}^{x_{i}} \right \}\).
Remark 7
Basis swaps are post-crisis financial products, which can only be priced in models accounting for the multiple curve nature of interest rates. In a single curve model, the price of a basis swap is zero; cf. Crépey et al. (2012, p. 181)
XVA equations
The pricing formulas in the previous subsection reflect valuation in an environment without counterparty credit risk, funding constraints, and other market frictions. In order to include the latter into the pricing framework, several value adjustments have been introduced: credit and debt valuation adjustment (CVA and DVA), funding valuation adjustment (FVA), as well as replacement cost (RC), among others. However, we disregard the capital valuation adjustment (KVA), that was introduced due to increasing capital requirements and the cost associated to them, and the margin valuation adjustment (MVA), arising when an initial margin is required, by assuming perfect hedging by the bank and the absence of initial margins. The various valuation adjustments are typically abbreviated by XVA, while we will refer to their sum as the valuation adjustment (VA), i.e.,
Our approach to the computation of VA closely follows the work of Crépey (2015a,b), while our exposition and numerical examples are based on Crépey et al. (2013), and Crépey et al. (2015, §5.1).
We consider two counterparties, called a bank and an investor in the sequel, that are both defaultable, and denote by τ b the default time of the bank, by τ i the default time of the investor, while we set τ=τ b ∧τ i ∧T. The default intensities of τ b ,τ i , and τ are denoted γ b ,γ i , and γ, respectively. We also consider the “full model” filtration \(\mathbb {G}\), which is given by \(\mathbb {F}\) enlarged by the natural filtrations of the default times τ b and τ i , and assume that the immersion hypothesis holds, that is, every \(\mathbb {F}\)-martingale stopped at τ is a \(\mathbb {G}\)-martingale.
The VA can be viewed as the price of a dividend paying option on the debt of the bank to the investor, paying off at the first-to-default time τ. Here, we have implicitly adopted the point of view of the bank. The VA from the point of view of the investor is similar, but not identical, due to, e.g., different funding conditions. The effective conclusion of Crépey (2015b) is that the VA in the setting described above can be computed in a “pre-default” framework, where the default risk of the counterparties appears only through the default intensities; see, in particular, Section 3 therein. More specifically, the VA Θ is the solution of the following BSDE under a martingale measure 

where r denotes the short rate process, P the clean price process, and g the VA coefficient. The overall price of the contract for the bank, in other words, the cost of the hedge incorporating the various risks, is then given by the difference between the clean price and the VA:
The VA coefficient g has the following form:
where \(\tilde \lambda _{t} = \bar {\lambda }_{t}-\gamma _{t}^{b}(1-\mathfrak {r})\), while each line on the right side corresponds to one of the four components of the VA. The parameters in the above equation have the following financial interpretation:
-
\(\gamma _{t}^{i},\,\gamma _{t}^{b}\), and γ t are the default intensities of the investor, the bank, and the first to default intensity, respectively.
-
ρi, ρb are the recovery rates of the investor and the bank to each other, and \(\mathfrak {r}\) is the recovery rate of the bank to its unsecured funder (which is a third party that jumps in when the banks’ internal sources of funding have been depleted; this funder is assumed to be risk free).
-
Q t is the value of the contract according to some valuation scheme specified in the credit support annex (CSA), which is a common part in an over-the-counter contract.
-
\(\Gamma _{t}=\Gamma _{t}^{+}-\Gamma _{t}^{-}\) is the value of the collateral posted by the bank to the investor.
-
\(b_{t},\,\bar {b}_{t}\) and \(\lambda _{t},\,\bar {\lambda }_{t}\) are the spreads over the risk free rate r t corresponding to the remuneration of collateral and external lending and borrowing (from the unsecured funder).
The value of the contract Q and of the collateral Γ, as well as the funding coefficients b and \(\bar {b}\) are specified in the CSA of the contract, which is used to mitigate counterparty risk. Different CSA specifications will result in different behavior of the VA; see Crépey et al. (2013, Sec. 3) and the next subsection for more details.
Remark 8
The immersion hypothesis implies weak or indirect dependence between the contract and the default times of the involved parties. Therefore, not every contract can be priced within the pre-default VA framework. As interest rate contracts exhibit weak dependence on the default times, this approach is appropriate for our setting; see also Crépey (2015b, Rem. 2.3).
XVA computation in affine LIBOR models
We are now interested in computing the value adjustments for interest rate derivatives, and focus on basis swaps as a prime example of a post-crisis product. The OIS forward rate and the forward LIBOR rate for each tenor are modeled according to the affine LIBOR models with multiple curves, and the model is calibrated to caplet data; see Grbac et al. (2015, §8) for details on the calibration of affine LIBOR models. An interpolating function is subsequently chosen and the dynamics of the short rate process are derived. Afterwards, the computation of the value adjustments is a straightforward application of the VA BSDE in (37).
This methodology allows us to compute option prices and value adjustments consistently since we only have to calibrate the discrete-tenor affine LIBOR model, while the dynamics of the short rate process, which is essential in the computation of the VA, follows from the interpolation. In particular, we do not need to introduce and calibrate (or estimate) an “exogenous” model for the short rate, as is done in other approaches. The interpolating function thus plays a crucial role in our methodology, since this is the only “free‘” ingredient once the affine LIBOR model has been calibrated. At the same time, it introduces an element of model risk, through the different possible choices of interpolating functions. In the sequel, we are going to examine the impact of different interpolating functions on the value adjustments.
The data we use for our numerical experiments correspond to the EUR market on 27 May 2013 and were collected from Bloomberg; see also Grbac et al. (2015, §8.4) for more details. The affne LIBOR model with multiple curves was calibrated to caplet data on a 10-year horizon, where the tenor lengths were 3 and 6 months. The driving affine process consists of three independent CIR processes. The sequences (u k ) and (v k ) were constructed so that they lie on a smooth manifold on \(\mathcal {I}_{T} \cap {\mathbb {R}}^{3}_{\geqslant 0}\); see Fig. 3. In particular, u k lies on straight lines for k∈{0,…,k1}∪{k2,…,k3}∪{k4,…,N} and on elliptical segments for k∈{k1+1,…,k2−1}∪{k3+1,…,k4−1}. The sequence u looks as follows:
where \(\bar u_{j}, \tilde u_{j}\in \mathbb {R}_{\geqslant 0}\) and satisfy \(\bar u_{j}\ge \bar u_{j+1}\) and \(\tilde u_{j}\ge \tilde u_{j+1}\) for all relevant \(j\in \mathcal K\); see (14) again. The structure of the sequence vx for each tenor x is analogous. In other words, short-term forward LIBOR rates are driven by all three components of the driving process X, medium term rates by two components, while long-term rates are only driven by the last component of X. Once the manifolds have been constructed, the sequences (u k ) and (v k ) were obtained by fitting the model to OIS and EURIBOR data from the same date. (Note that in this example we have N=40 and we chose k1=9,k2=16,k3=21, and k4=28.)
In order to illustrate the effect of different interpolating functions on the value adjustments, we consider three different specifications for the interpolating function U:
-
(IF1): Interpolation by fitting an entire forward curve (see Example 1);
-
(IF2): Linear interpolation between the u k ’s;
-
(IF3): Spline interpolation on sectors where all but one component of the vector u k are constant in k, and linear interpolation in between these sectors (i.e., when the u k ’s lie on curved segments of the manifold).
Let us now turn our attention to the computation of value adjustments. We consider a 3M-6M basis swap on the LIBOR, with inception at t=0 and maturity in 10 years. We follow Crépey et al. (2013) and consider five different CSA specifications, provided by
while the default intensities and spreads equal
The first three CSA specifications correspond to a “clean” recovery scheme without collateralization, since the value of the contract Q equals the clean price and there is no collateral posted. The fourth specification corresponds to a “pre-default” recovery scheme without collateralization, while the last one corresponds to a fully collateralized contract. Moreover, the first specification yields a linear BSDE in the VA Θ, which allows to use (forward) Monte Carlo simulations for the computation of the VA.
The price P t of the basis swap is provided by (36) for each \(t\in [T_{p_{1}}^{x_{1}},T_{q_{2}}^{x_{2}}]\), and we can observe that P t is a deterministic transformation of X t . Moreover, the short rate r t is a deterministic, affine, transformation of X t ; cf. (26). Therefore, the VA coefficient g t (r t ,P t ,Θ t ) is also a deterministic transformation of X t , and we can define a deterministic function \(\hat g\) such that
In other words, the VA BSDE is Markovian in this case, and the VA is also provided by the solution of a semi-linear PDE. In order to compute the VA for the basis swap numerically, we worked under the spot martingale measure  using a space grid consisting of 105 paths and a time grid with n=200 steps of step size h. We applied a backwards regression on the space-time grid, i.e.,
using a space grid consisting of 105 paths and a time grid with n=200 steps of step size h. We applied a backwards regression on the space-time grid, i.e.,

and approximated the conditional expectation using an m-nearest neighbors estimator with m=3. This choice turned out to be optimal when compared to (forward) Monte Carlo simulations in the case of a linear VA coefficient.
Discussion
The outcome of the numerical experiments is summarized in Figs. 4, 5 and 6. Starting with the top panel in Fig. 4, we observe that there are significant structural differences in the dynamics of the short rate due to the different interpolating functions; this is mostly visible when looking at the averages and the percentile lines. The bottom panel in the same figure displays the price process of the 3M-6M basis swap for the different interpolating functions. As the differences are not as clearly visible as before, we have plotted the absolute differences in prices due to the different interpolating functions in Fig. 5. There we see that notable differences in prices appear when using different interpolating functions (keep in mind, that the notional amount of the swap equals one, thus the deviations in prices are not negligible). As expected, the largest discrepancies between prices stemming from the first vs. second and the first vs. third interpolating functions occur on the curved section of the manifold used to construct (u k ) and (v k ). On the contrary, the discrepancies between prices from the second vs. third interpolating functions on the curved section of the manifold are zero, since both functions interpolate linearly in that segment.
Figure 6 depicts the sample path of the VA process using the first interpolating function (left panels) for the five different CSA specifications (top to bottom), while the other figures show the differences in the VA due to the different interpolating functions. The differences in the VA are one order of magnitude smaller than the differences in prices, however, the VA itself is an order of magnitude smaller than the basis swap price. Reflecting the situation for the prices, the largest discrepancies between VAs using the first and the other two interpolating functions occur around the curved section of the manifold. However, the discrepancies in the VA in the flat sections of the manifold are more pronounced than the corresponding discrepancies in prices. The reason is that the interpolation affects value adjustments both via the basis swap price and via the short rate used for discounting, and its effect is propagated in different segments through the backward regression. This becomes clear when one looks at the differences between prices and value adjustments stemming from using the second and third interpolating functions; although the difference in prices is flat zero, the difference in value adjustments is far from zero.
The numerical examples presented above show that the choice of the interpolating function entails significant model risk. The functions we chose are not especially far apart, in terms of their supremum norm, thus the differences above could become even higher. In fact, the coefficients of the short rate can become arbitrarily large due to the interpolating function. Therefore, both the manifolds on which the sequences u and v lie and the interpolating function have to be selected with caution, as they can fundamentally change the behavior of the model.
Appendix A
Time-integration of Affine processes
The following result is an extension of Theorem 4.10 in Keller-Ressel (2008).
Theorem 3
Let \(\theta \colon [0,T] \rightarrow {\mathbb {R}}^{d}_{\geqslant 0}\) be a bounded function and (X t )t∈[0,T] be an affine process on \(\mathbb {R}^{d}_{\geqslant 0}\), with functional characteristics F and R. Then \({\left (X_{t},\int _{0}^{t} \theta _{u} \circ X_{u} \mathrm {d} u\right)}_{t\in [0,T]}\) is a time-inhomogeneous affine process on \({\mathbb {R}}^{d}_{\geqslant 0} \times {\mathbb {R}}^{d}_{\geqslant 0}\) with functional characteristics
Here, ∘ denotes the componentwise multiplication between vectors.
Proof
Let \(n\in \mathbb {N}\), k∈{0,…,n}, and define \(s_{k}=\frac {k}{n}s\) and \(h=\frac {s}{n}\), hence s0,…,s n is an equidistant partition of [0,s] with step size h. Approximating the integral with Riemann sums and using the dominated convergence theorem, we have

Using next the tower law of conditional expectations and the affine property of X, A n can be written as follows

Iterating this procedure, we arrive at
with p0(u X ,u Y )=0, q0(u X ,u Y )=u X +hu Y ∘θt+s and
Using the generalized Riccati Eq. (3), we can expand ϕ and ψ linearly around the origin. Thus, we get
As θ is non-negative and bounded, the second part of the proof of Theorem 4.10 in Keller-Ressel (2008) remains the same. Hence, the recursive scheme above is an Euler-type approximation, starting from the terminal time, to the ODE
with initial conditions p(r,r,u X ,u Y )=0 and q(r,r,u X ,u Y )=u X , for all r≥0. □
References
Beveridge, C, Joshi, M: Interpolation schemes in the displaced-diffusion LIBOR market model. SIAM. J. Finan. Math. 3, 593–604 (2012).
Bichuch, M, Capponi, A, Sturm, S: Arbitrage-free XVA. Math.Finan. (2016). https://arxiv.org/abs/1608.02690.
Björk, T: Arbitrage Theory in Continuous Time. 3rd edition. Oxford University Press, Chichester (2009).
Brigo, D, Morini, M, Pallavicini, A: Counterparty Credit Risk, Collateral and Funding: with Pricing Cases for all Asset Classes. Wiley (2013).
Crépey, S: Bilateral Counterparty risk under funding constraints — Part I: Pricing. Math. Finan. 25, 1–22 (2015a).
Crépey, S: Bilateral Counterparty risk under funding constraints — Part II: CVA. Math. Finan. 25, 23–50 (2015b).
Crépey, S, Bielecki, TR: Counterparty Risk and Funding: A Tale of two Puzzles. Chapman & Hall/CRC Financial Mathematics Series. CRC Press, Boca Raton (2014). With an introductory dialogue by Damiano Brigo.
Crépey, S, Grbac, Z, Nguyen, H-N: A multiple-curve HJM model of interbank risk. Math. Financ. Econ. 6, 155–190 (2012).
Crépey, S, Gerboud, R, Grbac, Z, Ngor, N: Counterparty risk and funding: The four wings of the TVA. Int. J. Theor. Appl. Financ. 16(1350006) (2013).
Crépey, S, Grbac, Z, Ngor, N, Skovmand, D: A Lévy HJM multiple-curve model with application to CVA computation. Quant. Financ. 15, 401–419 (2015).
Cuchiero, C, Fontana, C, Gnoatto, A: Affine multiple yield curve models. Preprint. arXiv:1603.00527 (2016).
Duffie, D, Filipović, D, Schachermayer, W: Affine processes and applications in finance. Ann. Appl. Probab. 13, 984–1053 (2003).
Filipović, D: Time-inhomogeneous affine processes. Stoch. Process. Appl. 115, 639–659 (2005).
Glau, K, Grbac, Z, Papapantoleon, A: A unified view of LIBOR models. In: Kallsen, J, Papapantoleon, A (eds.)Advanced Modelling in Mathematical Finance – In Honour of Ernst Eberlein, pp. 423–452. Springer, Cham (2016).
Grbac, Z, Runggaldier, WJ: Interest Rate Modeling: Post-Crisis Challenges and Approaches. Springer, Cham (2015).
Grbac, Z, Papapantoleon, A, Schoenmakers, J, Skovmand, D: Affine LIBOR models with multiple curves: theory, examples and calibration. SIAM. J. Financ. Math. 6, 984–1025 (2015).
Jacod, J, Shiryaev, AN: Limit Theorems for Stochastic Processes. 2nd edition. Springer, Berlin Heidelberg (2003).
Keller-Ressel, M: Affine Processes: Theory and Applications to Finance. PhD thesis, TU Vienna (2008).
Keller-Ressel, M: Affine LIBOR models with continuous tenor (2009). Unpublished manuscript.
Keller-Ressel, M, Papapantoleon, A, Teichmann, J: The affine LIBOR models. Math. Financ. 23, 627–658 (2013).
Mercurio, F: Interest rates and the credit crunch: New formulas and market models. Preprint. SSRN/1332205 (2009).
Mercurio, F: A LIBOR market model with a stochastic basis. Risk.84–89 (2010).
Musiela, M, Rutkowski, M: Continuous-time term structure models: forward measure approach. Financ. Stoch. 1, 261–291 (1997).
Musiela, M, Rutkowski, M:Martingale Methods in Financial Modelling. 2nd edition. Springer, Berlin Heidelberg (2005).
Papapantoleon, A: Old and new approaches to LIBOR modeling. Stat. Neerlandica. 64, 257–275 (2010).
Acknowledgements
RW acknowledges funding from the Excellence Initiative of the German Research Foundation (DFG) under grant ZUK 64. Financial support from the Europlace Institute of Finance project “Post-crisis models for interest rate markets” is gratefully acknowledged.
Author information
Authors and Affiliations
Contributions
Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Papapantoleon, A., Wardenga, R. Continuous tenor extension of affine LIBOR models with multiple curves and applications to XVA. Probab Uncertain Quant Risk 3, 1 (2018). https://doi.org/10.1186/s41546-017-0025-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s41546-017-0025-4
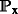 has exponentially-affine dependence on x; that is, there exist functions
has exponentially-affine dependence on x; that is, there exist functions 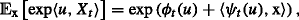
 satisfying Assumption (
satisfying Assumption (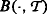 is a strictly positive special semimartingale and the left-hand limit process
is a strictly positive special semimartingale and the left-hand limit process 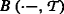 is also strictly positive, for every
is also strictly positive, for every 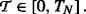
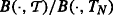 are
are  -martingales.
-martingales.
 . Right panel: using a linear interpolation
. Right panel: using a linear interpolation



